Ch3 - Bivariate Data

response varaible

measures the outcome of a study (dependent variable)

explanatory variable

attempts to explain the overserved outcomes (the independent variable)

describing a scatterplot

look for the overall pattern & striking outliers

describing/interpreting a scatterplot sentence

1 sentence: There is a [strong/moderate/weak] [positive/negative] [shape] relationship between [x-context] and [y-context].  There [do/do not] appear to be any outliers. 

1. strength (strong/moderate/weak) r-value

2. dir (pos or neg assoc)

3. shape (clusters, linear, curved, quadratic, log, etc)

   1. if dir. is pos. r is pos.

4. state outliers

5. context

pos association is

between 2 variables: when x axis variable increases, y axis variable increases

neg association

between 2 variables: when x axis variable increases, y axis variable decreases

correlation 

r → measures dir & strength of the linear relationship between 2 quantitative variables

• not impacted by stretch/shrink (like z its standardized)

• impacted by outliers

• can only discuss r see data/know linear

interpret/describe correlation

 There is a [strength], [direction] linear relationship between [variable1] & [variable2].

facts abt correlation

R

1. no distinction between explanatory (dependent) and response (independent)

2. both variables must be quantitative (makes no sense w/ categorical)

3. r has no units bc its standardized (ie z score doesn’t have units)

4. the sign of r matches the sign of slope

5. -1 <= r <= 1

6. r only measures strength & dir thru linear relation (correlation = 0 does not mean no relation just not linear ie circle)

7. correlation does not equal causation (only tru when random assignment)

y hat = a +bx

Least Squares Regression Line LSRS

• y hat = predicted value

• a = y-int (y coordinate)

• b = slope

linear relationship

interpret/describe predicted value (y hat)

[y-hat] is the predicted value of [response variable y] when [explanatory variable] is [input amount]. 

interpretations =

“predicted”

Extrapolation

is the use of a regression line for prediction far outside the domain & range of the data to obtain the line

• usual = inaccurate predictions

a residual is

the diff between the observed value & the predicted value (regression line)

• residual = y - y hat

• actual - predicted value

a good regression line makes residuals as small as possible

interpret/describe residual

The actual/true [y-context] is [higher/lower] than the predicted [y-context] by [residual].

interpret/describe the slope of a regression line

(b):  As [explanatory variable] increases by one [unit], the predicted [response variable] [increases/decreases] by [b] [units]. 

interpret/describe the y-int of a regression line

(a):  When [x-context] is zero, the predicted [y-context] is [a] [units].

interpret/describe the standard deviation of the residuals

When using the LSRL, the predicted number of [y-context] is typically [s units] off from the actual number. 

A Least Sqaure Regression Line

(LSRL) tries to minimize the sum of the squared residuals (as small as possible)

• the mean of the residuals is always 0

• the LSRL always goes thru the point (x bar, y bar)

use for summary data

defining y hat

y hat = “predicted __ units”

Calc Steps (LSRL)

• Stat → calc → option 8

• stat → calc → option 8 → store rest → var → y → 1 (graphs line)

use when given table data

r²

coefficient of determination: the square of the correlation coefficient describes the strength (not dir.) of a linear relationship

• measures how closely the points fall to the LSRL

r² =

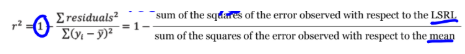
interpret/describe the coefficient of determination

About [r²] % of the variability in [y-context] is accounted for by the least-squares regression line. 

residual plot

is a scatterplot of the residuals agaisnt the explanatory variable → if it is linear there will be a random scatter on plot

residual plot on calc

1. run linear regression!

• 2nd statplot → 1 → Xlist (list of explanatory, 1) → Ylist → 2nd stat → bottom!