CSE 2221 Midterm 2 Ultimate Study Guide

Vocabs from all lectures

NaturalNumber

a component group that lets you work with whole numbers (numbers like 0, 1, 2, 3, etc.). It acts like a tool or a way to do things with these numbers (interface)

interface

Description of the boundary between a system and everything else

standard interface

contains standard methods that are part of most (nearly all) OSU CSE component families:

clear()

newInstance()

transferFrom()

Single point of control over change

having one central place to make and manage changes in software, making it easier to update and control the software effectively (Think standard interface).

kernel (primary) methods

• Minimal set of methods that are primitive (baseline) for NN: isZero(), multiplyBy10(), divideBy10

• Primary methods can be used to make secondary methods

Secondary methods

• usually more robust or versatile compared to the kernel methods

• they are added to the component family to make it easier to use in everyday client code

mathematical model

• a structured representation of a real-world situation or system using mathematical equations, formulas, or symbols

• emphasizes the importance of specifying any limitations or conditions (constraints) that affect the possible values within the model

constraints

limitations or restrictions that impose rules or conditions on certain aspects of a system or model, specifying what is allowed or not allowed.

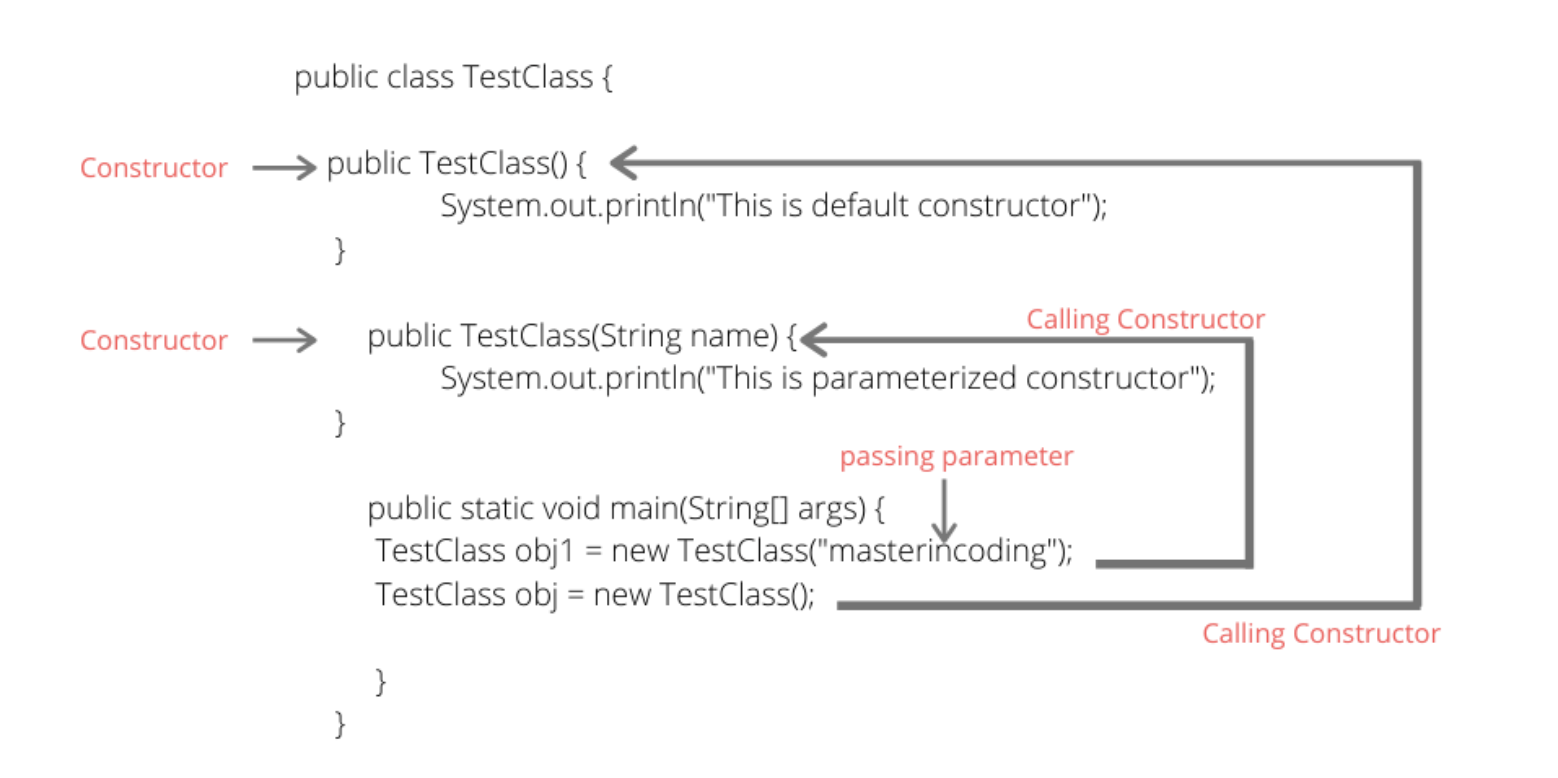
constructors for NN

• Special methods used for the creation of an object.

• There are four types of constructors for each implementation class:

1. No-argument constructor:

   ensures: this = 0

2. Copy constructor:

   ensures: this = n

3. Constructor from int:

   requires: i >= 0

   ensures: this = i

4. Constructor from string:

   requires: there exists n: NATURAL

   (s = TO_STRING(n))

   ensures: s = TO_STRING(this)

constructors

Special methods used for the creation of an object

instance method

methods defined under a class and we can call such functions only after creating an object of that class

All the methods for NaturalNumber are

instance methods

n.methodName(arguments) (What is n, arguments, this?)

• where n is an initialized variable of type NaturalNumber

• n is going to be the receiver on this, and then everything else it'll it can refer to itself as this inside that method

• for all instance methods, the corresponding distinguished formal parameter implicitly has the name this.

distinguished formal parameter

refers to a special parameter in an instance method called this

receiver

the thing that receives the call for one of its methods. It can be a package or an object

parameter mode

• Javadoc contract tags

• refers to the way in which a argument is modified in a function or method

• the parameters of updates, replaces, restores, and clears

mutable

subject to change in updates, replace, and clear-mode parameter ()

In a ensures clause, a # in front of a variable whose value might be changed is pronounced "old";

#this denotes the old, or incoming, value of this

primitive type

• built-in, fundamental data types

• they represent simple values and are not objects

• examples include boolean, char, int , & double

• They have a fixed size and are typically stored directly in memory

reference types (or class types)

• Encompass all other types in Java that are not primitive

• They are used to create objects and represent more complex data structures

• Examples include String, custom classes like NaturalNumber, and other user-defined types (SimpleReader, SImpleWriter, etc.)

• They are like labels that show where objects are kept in the computer's memory, usually in a place called the "heap"

There is no limit on the number of other _________ types that can be developed

user-defined

primitive variable

Variable that represents a single value

reference value

stores the memory address of an object

reference

location in memory which points to the object

object

contains the value of the class (what is referred to by the reference)

memory address

A specific location in memory where instructions or data are stored

object value

a class instance that does not have an identity

String s = “go“ vs s → “go“

The → sign means that s is a reference to the object go

primitive variables

Can store data values

anonymous primitive variable

Variables without names (think literal ints, strings, etc)

uninitialized primitive variables

a variable that is declared but is not set to a definite known value before it is used.

anonymous reference variable

A literal, which has an object value but no name

uninitialized reference variable

A reference variable which has been created but hasn't been assigned a value

garbage collector

“reclaim” or “recycle” the memory where an unreferenced temporary object is stored

aliases

two or more references that refer to the same object

immutable types

types for which no method might change the value of the receiver, or any other argument of that type

mutable types

types for which at least one method might change the value of the receiver, or some other argument of that type

==

compares reference values

arrays are...

• reference types

• The name of the array (e.g., a in the example) is a reference to the entire collection of element variables a[0], a[1], …, and a.length

arrays using .equals()

does not actually compare arrays “element-wise“ but rather is equivalent to == and compares reference values

package

• a namespace that organizes a set of related classes and interfaces; ex: java.util

contract details

• Contracts in the APIs for OSU CSE components include these important features:

• Parameter names in requires and ensures clauses always stand for the object values, never the reference values, of the corresponding arguments to a method call

• Reference-type arguments are always non-null

arguments

values that are passed into a method call

parameter modes

There are 4 parameter modes, each of which indicates a possible way that a method might change the value of the corresponding argument. Parameter modes help in 3 ways:

1. concisely summarize which arguments might have their values modified by a call

2. make requirements/ensures clauses shorter

3. allow us to perform sanity checks of contracts against simple errors

restores-mode

Restores the parameter back to its original incoming value

default parameter mode

a way to set default values for function parameters a value is no passed in (ie. it is undefined)

clears-mode

Sets the parameter to an initial value of its type as though there was a no-argument constructor (for NN this is 0)

replaces-mode

Has a value that might be changed from its incoming value, but the method's behavior does not depend on its incoming value

updates-mode

has a value that might be changed from its incoming value, and the method's behavior does depend on its incoming value

null reference

a reference that does not refer to any object

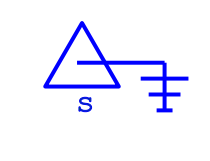
simple assignment

assigns the value or variable on the right to the variable on the left; variable = expression (→ in tracing table)

parameter passing

The process of assigning an argument value to a parameter variable.

Aliasing from parameter passing

Because a formal parameter of a reference type is initialized by copying the corresponding argument’s reference value (which is tantamount to assignment of the argument to the formal parameter), parameter passing is another source of aliasing

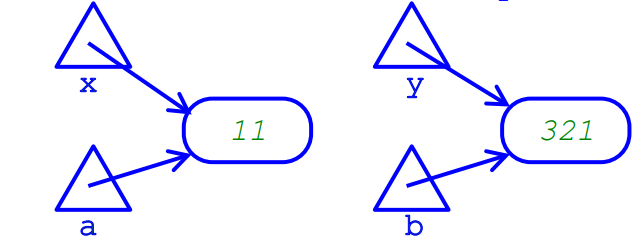
repeated arguments

sending the same reference as two different arguments in a method; same if passing a reference to itself through a method, i.e. n.add(n)

it would be impossible for any implementation of foo to produce the outcome supposedly ensured according to its contract

DO NOT DO REPEATED ARGUMENT. It is the fault of the client.

contract

• an agreement that the class will expose certain methods, certain properties, and certain behaviors

• a specification of its intended behavior

floor of s

a notation which means the greatest integer less than or equal to s; for non-negative s, it is also known as the integer part of s. (Example: ⌊4.47⌋ = 4)

interval halving (aka bisection or binary search)

each iteration eliminates half of a previous interval

mathematical strings

• A string can be thought of as a series of zero of more entries of any other mathematical type, say, T (T is called an entry type)

• Similar to an array

• ex: <1, 2, 3, 2>, <'G', 'o'>, <>

Remember mathematical strings don’t have to be of type String

entry types

Can be elements, but they don't have to be; an element name, an amount, or a date For example, string of T where T is the entry type

Math notation for strings

• The following notations are used when we write mathematics (e.g., in contract specifications) involving strings.

• Notice two important features of strings:

  • There may be duplicate entries (in fact, there may be arbitrarily many of a given entry value)

  • The order of the entries is important

empty_string

• The string "", which contains no characters and has a length of zero.

• A string with no entries at all, is denoted by < > or by empty_string

Denote the string “go“…

<‘g‘, ‘o‘>

Mathematical string concatenation

linking into chains, uses the * symbol

• Examples:

  < 1, 2 > * < 3, 2 > = < 1, 2, 3, 2 >

  < 'G', 'o' > * < > = < 'G', 'o' >

  < > * < 5, 2, 13 > = <5, 2, 13 >

  < > * < > = < >

Substring, Prefix, Suffix of mathematical strings

•We say s is substring of t if the entries of s appear consecutively in t

• We say s is prefix of t if the entries of s appear consecutively at the beginning of t

• We say s is suffix of t if the entries of s appear consecutively at the end of t

Use “is not“ for negation

length

The _____ of a string s, i.e., the number of entries in s, is denoted by |s|

Examples:

|< 1, 2, 3, 2 >| = 4

|< 'G', 'o' >| = 2

|< >| = 0

Notation for substrings of mathematical strings

The sub-string of s starting at position i (inclusive) and ending at position j (exclusive) is denoted by s[i, j)

Examples with s = "GoBucks":

s[0, |s|) = "GoBucks"

s[2, |s|-1) = "Buck"

s[1, 1) = ""

s[2, 3) * s[5, 7) = "Bks"

Notation for reverse of mathematical strings

The reverse of a string s, i.e., the string with the same entries as s but in the opposite order, is denoted by rev(s)

Examples:

• rev(< 1, 2, 3, 2 >) = < 2, 3, 2, 1 >

• rev(< 'G', 'o' >) = < 'o', 'G' >

• rev(< >) = < >

Notation and meaning for permutations of mathematical strings

an arragement or listing in which an order or placement is important; denoted by perms (s1, s2)

• Examples:

  perms(< 1, 2, 3 >, < 3, 1, 2 >)

  not perms(< 2, 2, 1 >, < 2, 1 >)

  perms(< >, < >)

Notation for occurrence count of mathematical strings

Counts the number occurrences of specific text, such as terms, phrases, numbers, or expressions in a larger text; denoted by count (s, x)

• Examples:

  count(< 2, 2, 2, 1 >, 2) = 3

  count(< 2, 2, 2, 1 >, 4) = 0

  count(< 'G', 'o' >, 'G') = 1

  count(< >, 13) = 0

recursion

When a function calls itself

implement

indicates a relationship between a class and an interface; it is making a commitment to provide concrete implementations for all the methods defined in that interface

If C implements I then class C contains code for the behavior specified in interface I

extends

• signifies an inheritance relationship.

• may hold between:

  – Two interfaces or two classes

inherits

a fundamental concept in object-oriented programming where one class or interface takes on the attributes and behaviors (methods) of another

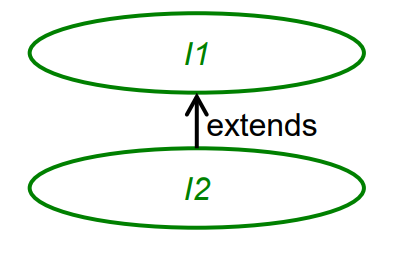
What terms an be used to describe the relationship between interfaces of ssI1 and I2 (6)

• I2 is a subinterface of I1

• I2 is a derived interface of I1

• I2 is a child interface of I1

• I1 is a superinterface of I2 s

• I1 is a base interface of I2

• I1 is a parent interface of I2

class extension

serves two purposes:

1. To add method bodies that are not already in the class being extended (similar to the use of extension for interfaces)

2. To override methods that are already

   implemented in the class being extended, by providing new method bodies for them

override methods

refers to the practice of providing a new method body in a derived (or child) class for a method that is already implemented in the base (or parent) class

overload

refers to the ability of a class to have multiple methods with the same name, but with different parameters

relationship between C1 and C2 (6 answers)

• C2 is a subclass of C1

• C2 is a derived class of C1

• C2 is a child class of C1

• C1 is a superclass of C2

• C1 is a base class of C2

• C1 is a parent class of C2

When writing the code for the body of either a method whose contract is from an interface being implemented, or that overrides a method in a class being extended, you preface the method body with an _________.

@Override annotation

Interface as declared type

When a variable is declared using the name of an interface as its type,

e.g.: NaturalNumber k = new NaturalNumber2(); then its declared type (or static type) is said to be an interface type

NaturalNumber is the interface, NaturalNumber2 is the class

class as declared type

When a variable is declared using the name of a class as its type,

e.g.: NaturalNumber2 k = new NaturalNumber2(); then its declared type (or static type) is said to be a class type

Object Type

When a variable is instantiated (an object for it to reference is constructed), e.g.: NaturalNumber k = new NaturalNumber2(); then its object type (or dynamic type) is the class type from which the constructor comes.

In this example the object type of k is NaturalNumber2.

instantiated

a call the constructor of a class that creates an instance or object of the type of that class

object type (or dynamic type)

a variable or an expression is the type of its value during runtime, when the program is being executed. It may change as the program is executed

polymorphism

having many forms

• Example 1:

  NaturalNumber k =

  new NaturalNumber2();

  NaturalNumber n =

  new NaturalNumber2Override();

  ...

  k.power(2);

  n.power(2);

  ...

• Example 2:

  NaturalNumber k =

  new NaturalNumber2();

  NaturalNumber n =

  new NaturalNumber2Override();

  NaturalNumber j = k;

  ...

  j.power(2);

  …

common features with static and instance methods:

• May have formal parameters, of any types

• May return any type, or nothing (void)

• May be public or private

• May compute the same things

  • Arguments are passed to all calls using

    the same parameter-passing mechanism

static methods

• Are declared with the keyword static

  - Suppose power is a static method declared in the class NNStaticOps

  - Its declaration might look like this:

  public static void power(NaturalNumber n, int p)

  {...}

• Are called without a receiver

  - A call to power from within the class

  NNExtraOps might look like this:

  power(m, k);

  - A call to power from outside the class

  NNExtraOps might look like this; i.e., before

  a dot, the method name is qualified with the

  name of the class where it is declared:

  NNExtraOps.power(m, k);

instance methods

• Are declared without the keyword static

  - Suppose power is an instance method

  declared in the class NNExtraOps

  - Its declaration might look like this:

  public void power(int p)

  {...}

• Are called with a receiver

  - Suppose m is a variable of dynamic/object

  type NNExtraOps (or, it turns out, any type

  that extends NNExtraOps)

  - Then a call might look like this; i.e., before a dot is the name of the receiver of the call:

  m.power(k);

confidence building approach

an argument that the code is correct (i.e., correctly implements its contract)

size metric

allows you to argue that a smaller problem is being solved by each recursive call in your code

A formal version of this argument follows the proof technique known as…

mathematical induction

proof by contradiction

assumes the statement to be proven is false, and work to show its falsity until the result of that assumption is a contradiction

Structure of Trees

Two views of a tree:

- A tree is made up of:

• A root node

• A string of zero or more child nodes of the root, each of which is the root of its own tree

• A string of zero or more subtrees of the root, each of which is another tree

expression tree

a representation of a formula you might type into a Java program or into a calculator

order of evaluation

a collection of rules that reflect conventions about which procedures to perform first in order to evaluate a given mathematical expression

operator

signs, e.g., +, -, *, /

operand

numbers, e.g., 1, 2, 3, 4, & 5

expression tree

a representation of expressions arranged in a tree-like data structure

unit testing

• to test individual units or components of software (one class, one method at a time)

• the unit being tested is known as the UUT, or unit under test

integration testing

testing what happens when multiple components are put together into a larger system