Decision Trees

classification techniques

1. decision tree methods

2. nearest neighbor

3. neural networks

4. naive bayes

5. support vector machines

what is a decision tree?

1. classifier w tree structure

2. essentially a flowchart (each ex moves from root to leaf)

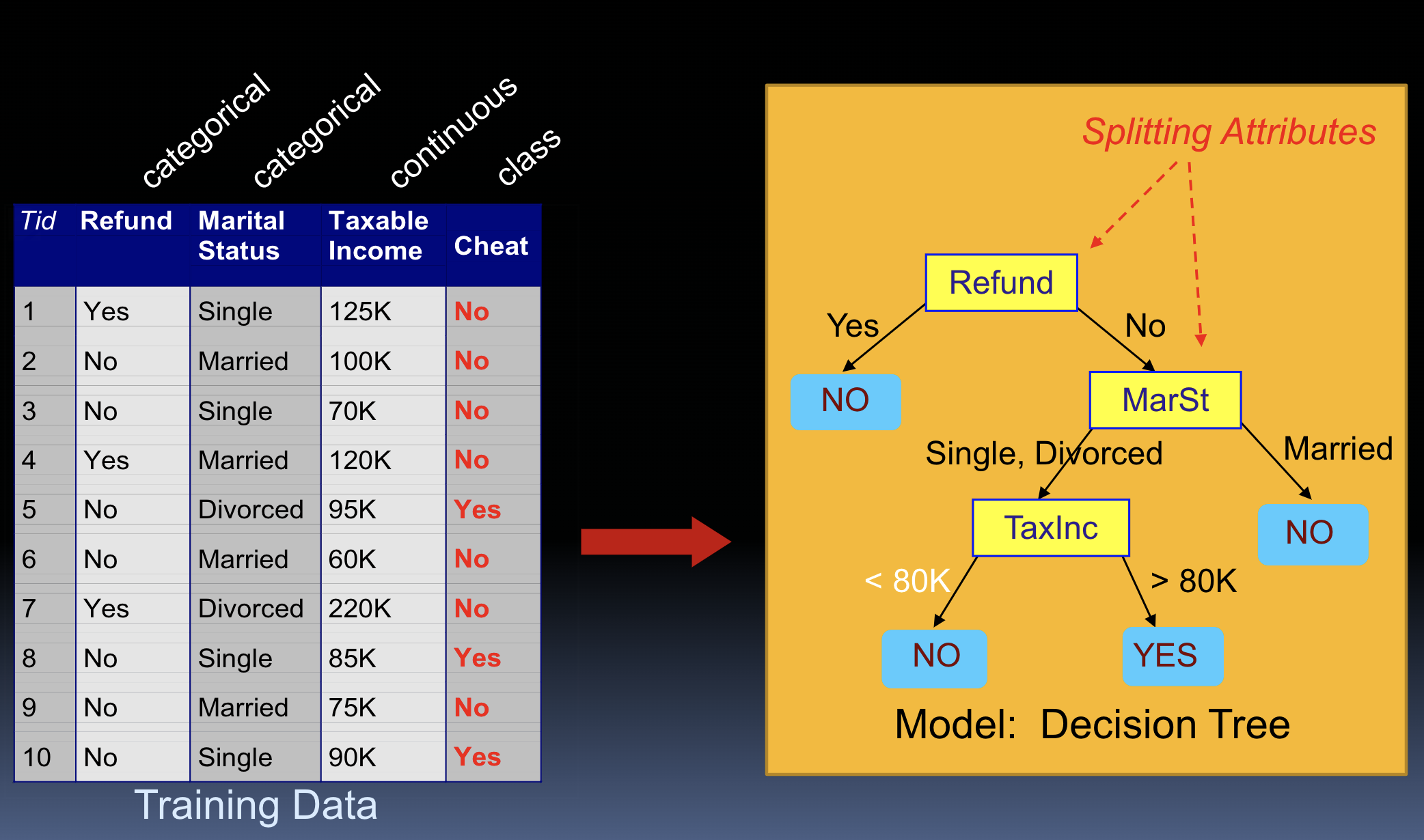
DT definitions

1. root node- start point

2. decision node- test on single attribute

3. leaf node- indicates value of class

4. path- disjunction of conditions to make final decision

2 phases of tree generation

1. tree construction

   • at start all training ex are at root

   • partition ex recursively based on attributes alg selects

2. tree pruning

   • improves performance on new examples

   • best tree on training data may not be best on new test data due to overfitting

decision boundaries

-DTs form rectangular regions → each region is a leaf

-border b/n regions = decision boundary

-decision boundary = axis parallel

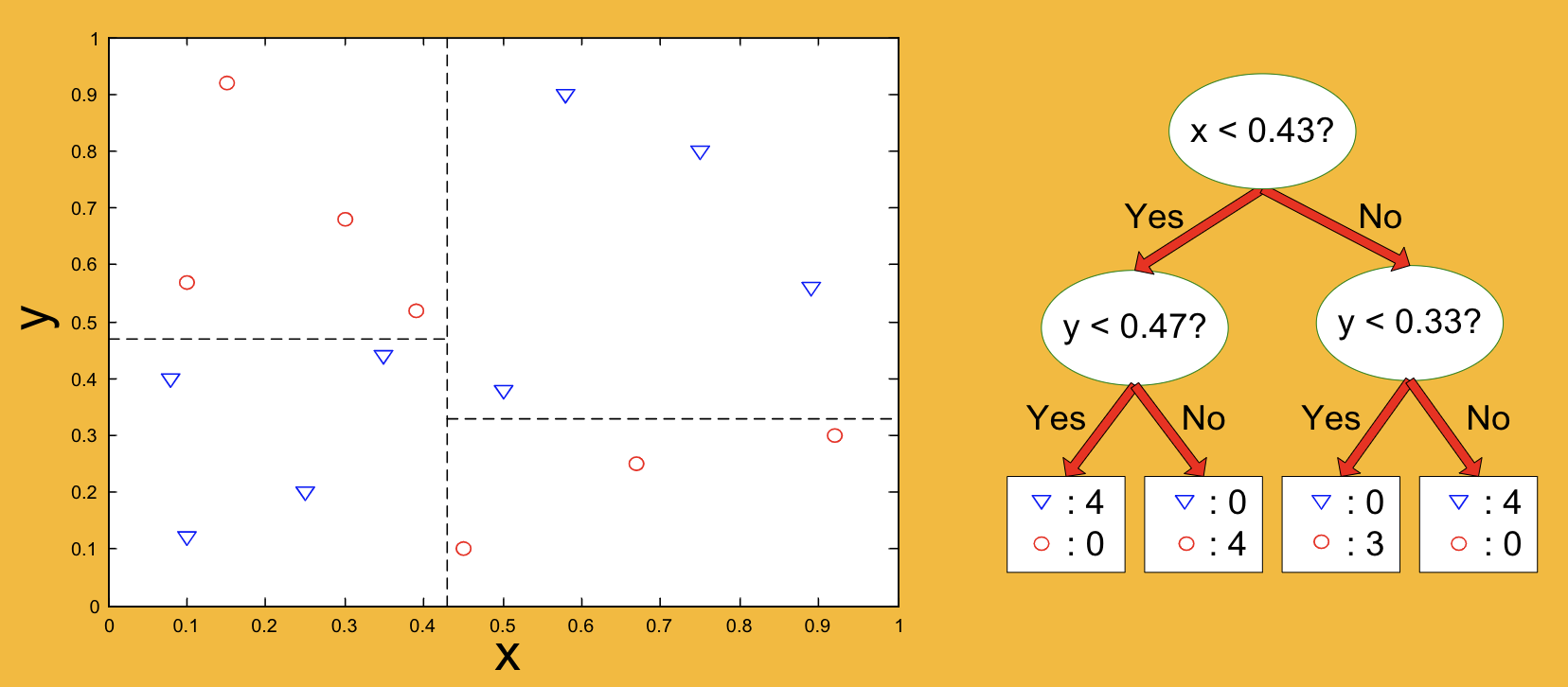
expressiveness

flexibility of the classifier in forming decision boundaries

• linear models- form boundaries w 1 line/plane

• DTs- form rectangular regions

are linear models or DTs more expressive?

DTs- form many regions

• but can only form axis parallel and linear can form 1 angled linear boundary

• so depends on model which is more appropriate

downside to flexibility?

can lead to more overfitting

when are DTs good?

strong interactions b/n many features (accurate modeling=must have complete trees)

when are DTs bad?

target class based on continous funcs that involve 2 variables (unless simple)

DT learning concept x<y

-not good → cannot learn perfectly unless tree has infinite # leaves

-can only approximate w many small rectangles

tree construction

top-down recursive; divide and conquer

• start w all training ex at root

• partitioned recursively based on selected attribute

  • best attr selected using a metric

• recursive process

  • partition ex at root based on ‘best’ feat

  • if binary split recurse on right then left child, etc

tree building is

greedy

• each decision = locally optimal (not globally)

• 1-level lookahead

• heuristic methods = for difficult problems

• benefit to greedy heuristic = fast

splitting on categorical attributes

1. multi-way split- split on every value

2. binary split- divides into 2 subsets

splitting on continous attributes

1. partition dynamically into ordinal values using equal freq or width

2. binary split- (A<v) or (A>=v); sort #s and try each split b.n successive #s

when does tree construction/partitioning/splitting stop?

1. all samples at a node belong to same class

2. no remaining attributes to split on (majority voting used to assign class)

3. no ex left

4. stop when not beneficial to split (basic method ignores and handles w pruning but pre-pruning does this)

picking locally optimal split

hunt’s alg- recursively partition training records into successively purer subsets

• pure(homogeneous) set f all ex belong to same class

• there are levels of purity

which split is best ex.

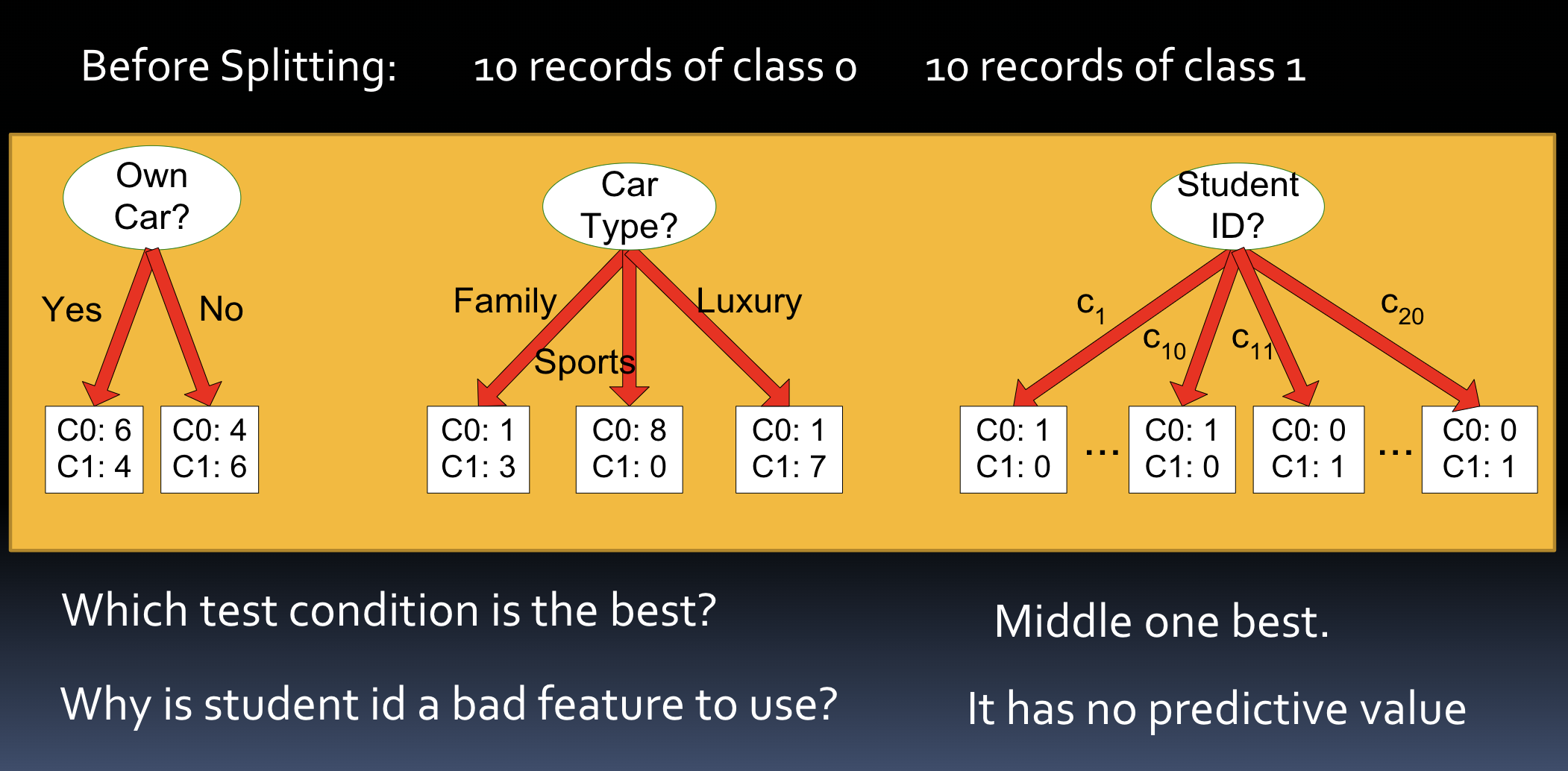
purity is measured using

statistical metric

• entropy

• gini

• classification error rate

avail DT algs

1. hunt’s alg (one of earliest)

2. CART (classification and regression trees)

   • regression tree- can predict numerical value so not just a classifier

   • sklearn

3. ID3, C4.5 (pretty old)

converting DT to rules

1 rule = per leaf

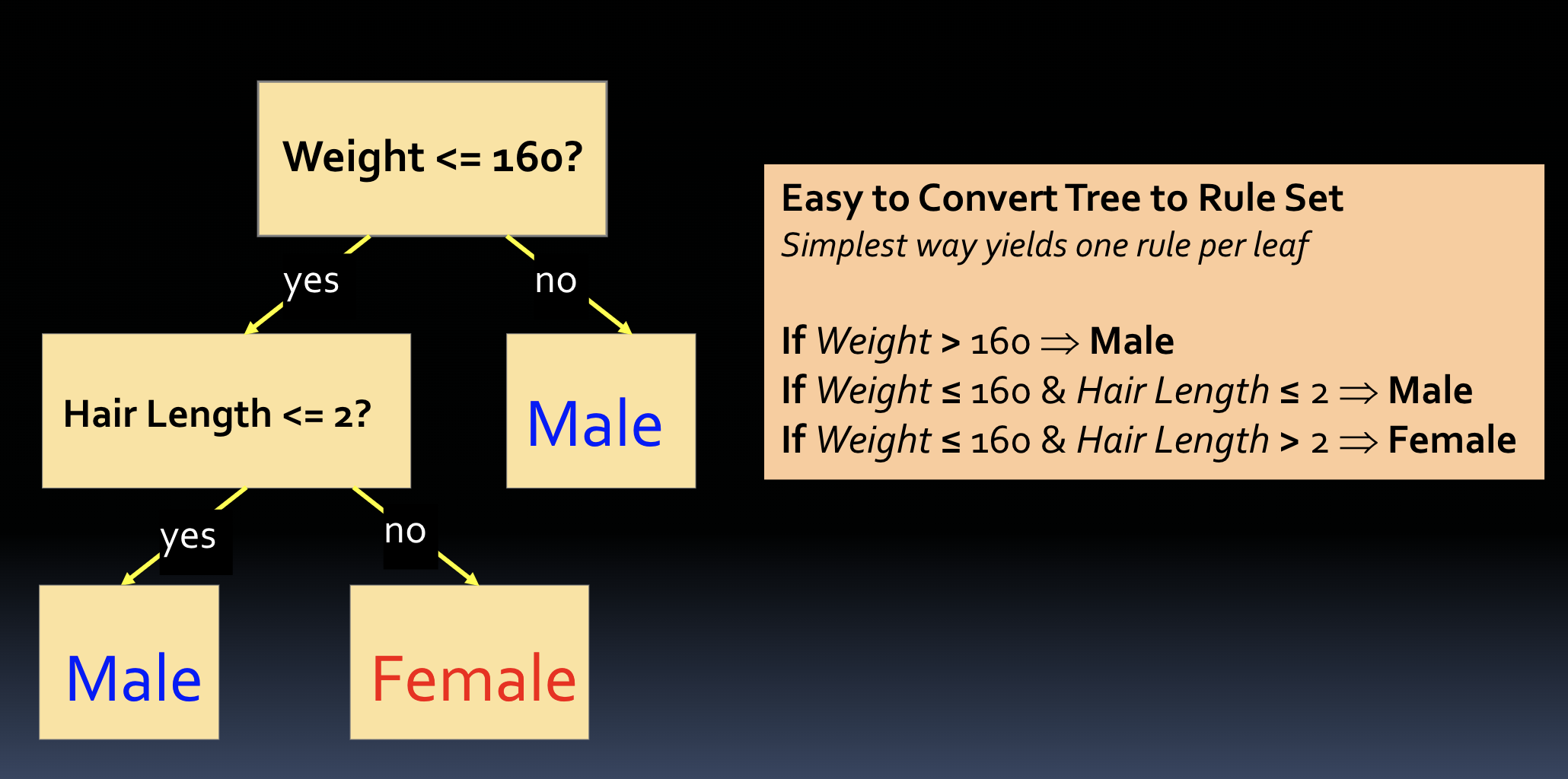
DT algs in practice

-Weka = free open source java DM suite

-Python Scikit includes DT alg = based on CART; doesnt handle categorical data so need to convert to #s

entropy

-measures impurity/randomness of set of examples

-range from 0 (least random) to 1 (most)

-want close to 0 in classification

entropy is 0 if outcome is

certain

entropy is maximum if

we have no knowledge of system ( / any outcome is equally possible)

we want entropy to be

low → more orderly

entropy to select feature

-entropy defined on a sample (entire training set aka root or sample aka one leaf)

-consider entropy after DT split to identify best feature to split on (c samples for a c-way split)

-use information gain that measures reduction in entropy → split on feature w max info gain

information gain

entropy of parent - entropy of children

• k-way split → k child nodes

• sum child entropies weighted by relative freq (weighted avg)

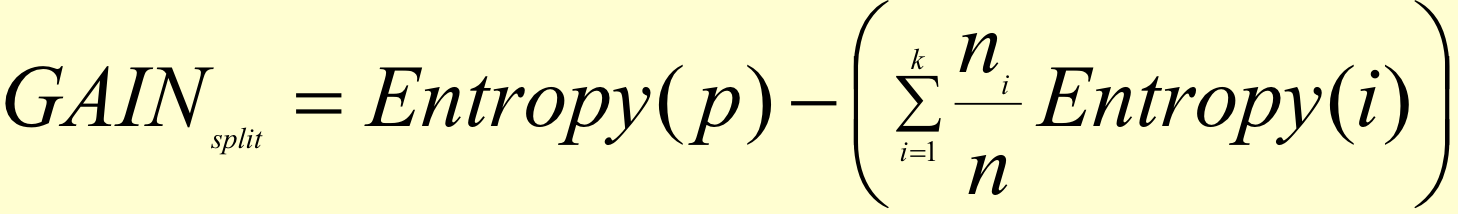
log₂x calculations

log₂x = log₁₀x/ log₁₀2

log₂x=log₁₀x/.301

GINI index

-node t with c splits

-like entropy (lower=better)

-split on feature w lowest GINI after split

-compute weighted GINI avg of childnre

-0 is best, 0.5 is worst

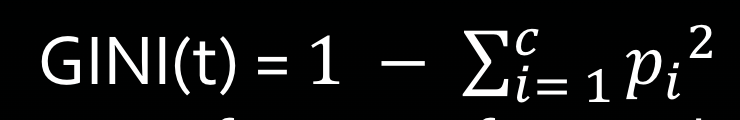
classification error rate

-at a node t

-classify node based on most freq value, count errors, and divide by # of ex

-measures misclassification error made by a node

• for binary- 0 (best), 0.5 (worst)

• for k splits- 0 (best), 1-1/k (worst)

  • 5 splits = 0.8 error rate

-must compute error rate of children after split

splitting metric comparison

comparison for 2 class problem as probability p of one class varies

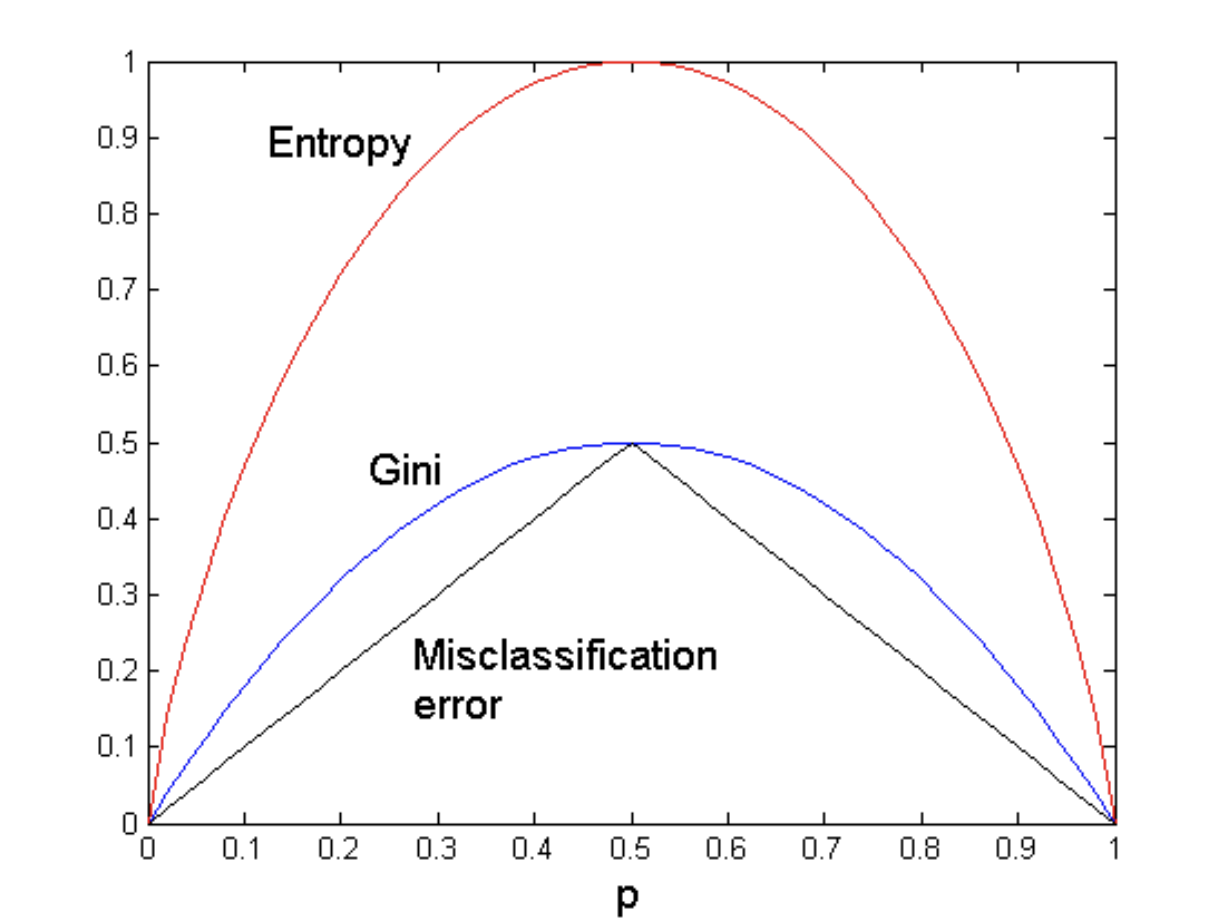
error rate often used to evaluate results, but never for

selecting features

• DT use a greedy strat to we need to use splitting metric for globally better results

occam’s razor

-among competing hypotheses → one with fewest assumptions should be selected

-complex models = greater chance it was fitted accidentally by errors in data (consider complexity when eval model)

errors

1. training errors- errors on training set

2. test errors- errors on test set

3. generalization errors- expected error of model over random selection of ex from same distribution (measured using test set)

model overfitting occurs when

model too complex

• may minimize training errors at expense of more test set/generalization errors

• difficult to predict when this will occur

overfitting ex) Ohm’s law

says V=IR (current b/n 2 points=directly proportional to voltage and inversely proportional to resistance)

underfitting

model is too simple → training and test errors large

overfitting

model is too complex → training error low but test error high

• good for training error

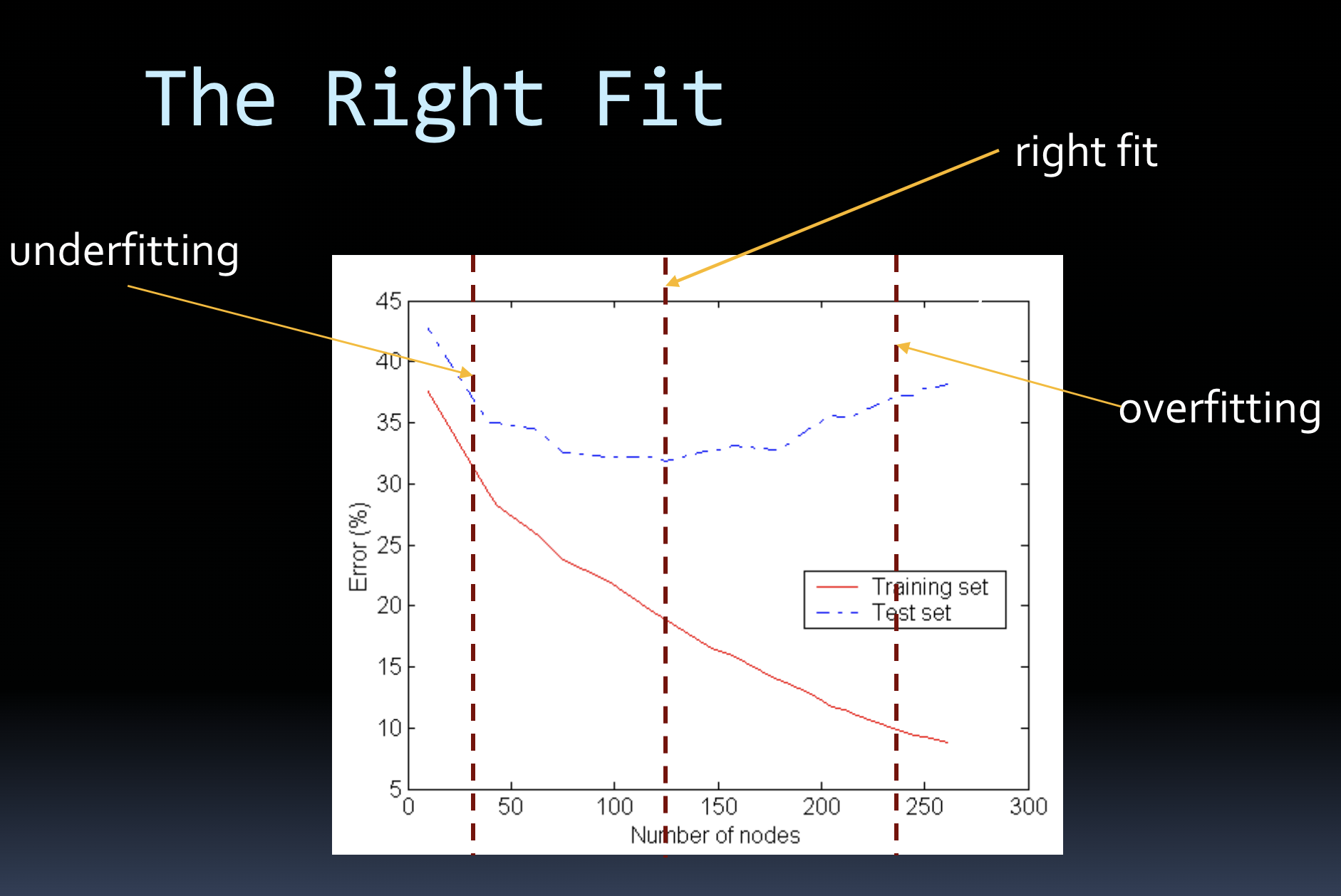
the right fit

in figure- best generalization performance around 130 nodes (test set error rate=lowest)

a synthetic data set

a data set artificially generated for which we know the correct underlying concept

• if condition met → class +

• if not → class -

• data set defined using gaussian distribution

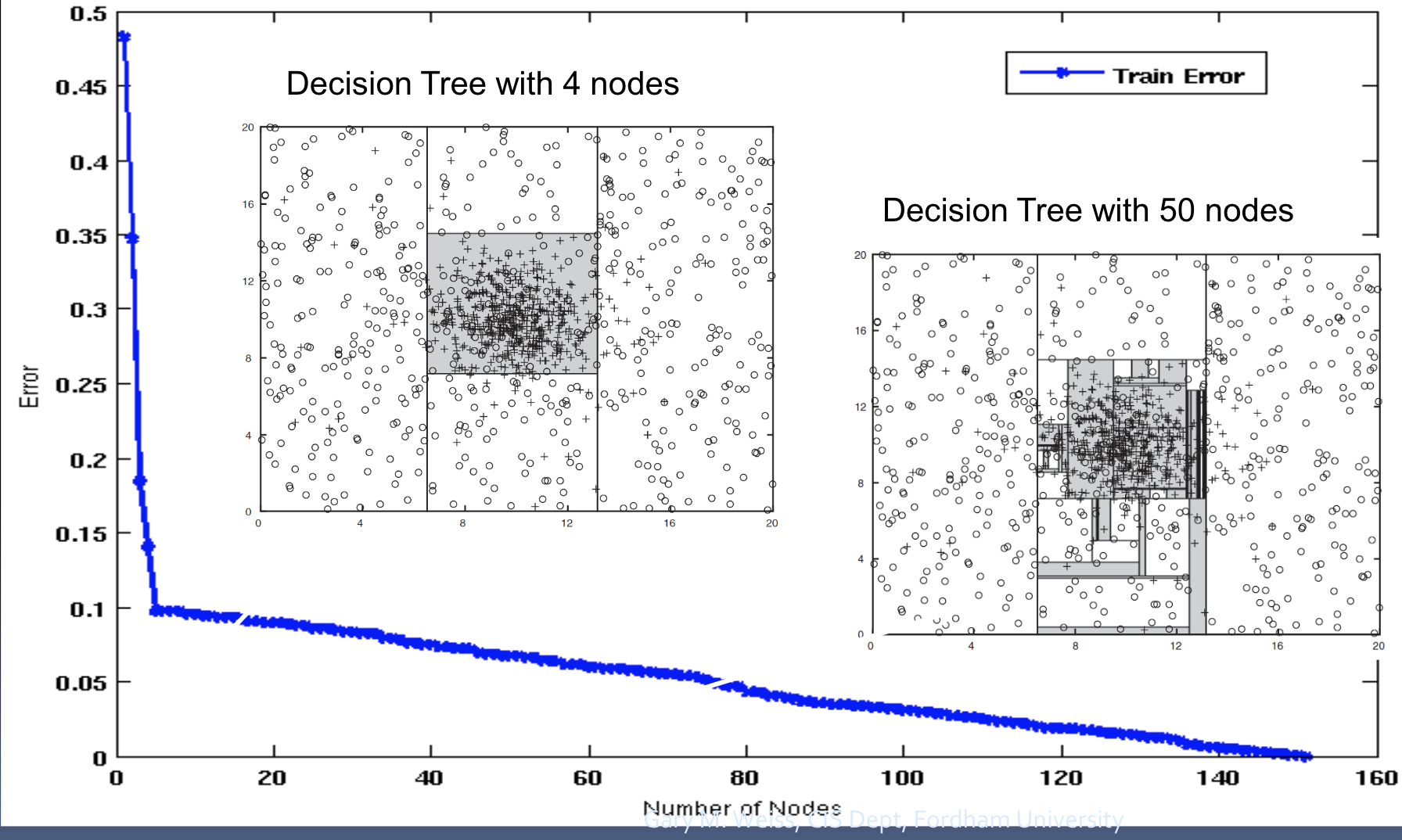
determine which tree is better

look at generalization (test set) error

in ex) 50 nodes cover many areas outside gaussian region and covers noise → 4 nodes prob better

if you have more training examples to learn from you have more

data → more complex model

inc amt of training data allows

DT to identify new regions of concept to be learned (more complex model can be okay)

what will generally happen to test set performance w more training data?

improves → more data=good

more data leads to more complex (usually better) models,

but not overfitting

overfitting avoidance strategies

1. pre-pruning- avoid overfitting in tree building process

   • difficult, rarely used

2. post-pruning- allow tree to overfit data then prune it back

   • common

pre-pruning strategies

-early stopping criteria

• if class distribution is independent of avail features

• if splitting node does. not improve purity (use info gain / gini)

• assign penalty for model complexity and stop when benefit does not outweigh penalty

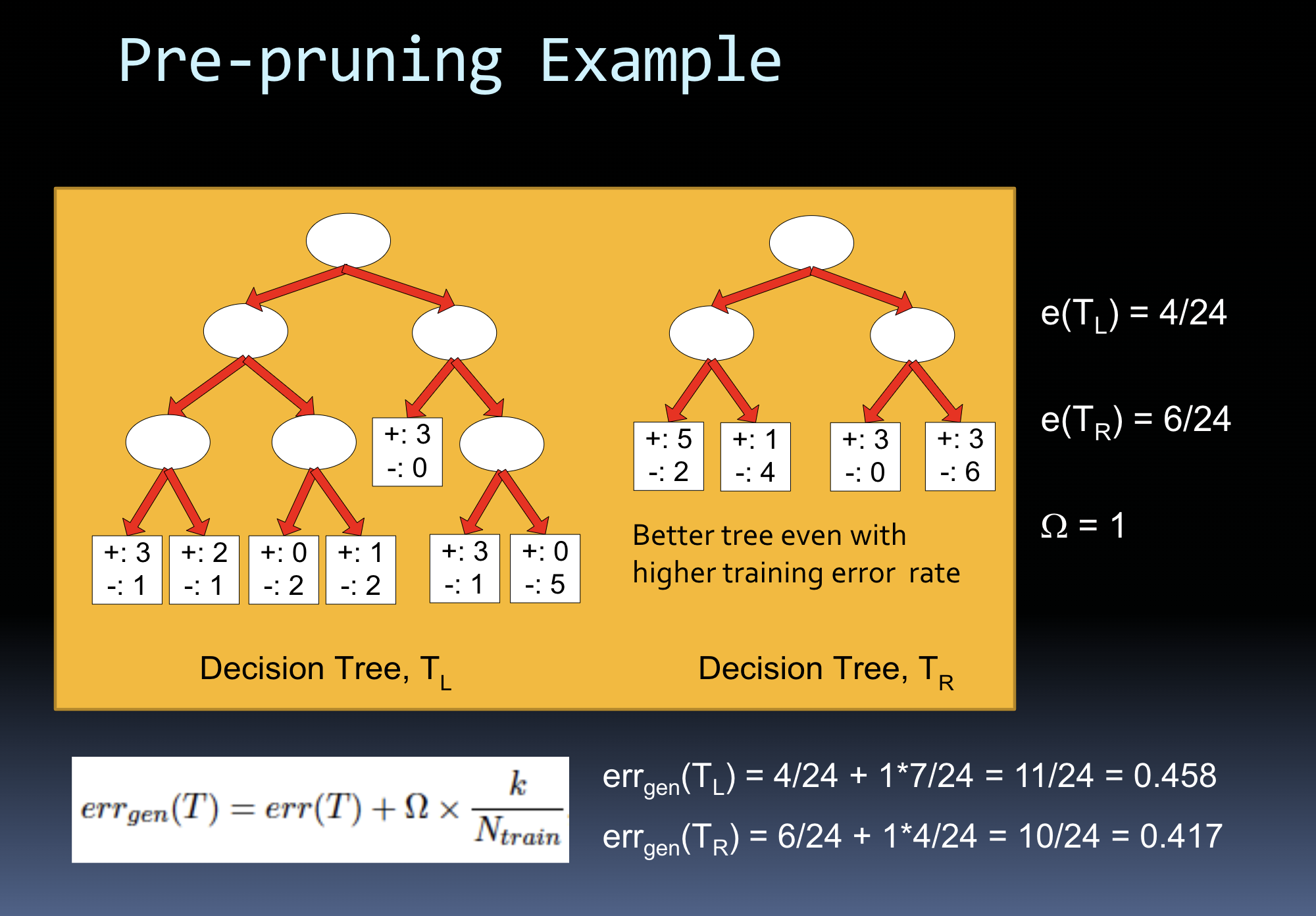
pre-pruning with complexity estimate

generalization error(model) = training error(model) + a x complexity(model

• training error(model)=optimistic

  • reasonably the best to hope for on test set

  • error rate will be higher

pessimistic error estimate

generalization error rate

minimum description length (MDL)

-imagine u need to transmit dataset; options:

1. send entire data set

2. send complex model with no/few errors

3. send simpler model and misclassified ex

-best option=requires fewest bits=MDL

-tradeoff b/n complexity and errors = less arbitrary than for prepruning

post-pruning

-grow DT w few limits and then trim in bottom-up fashion

• reduced error pruning- replace subtree w leaf node if generalization error will improve (improvement assessed w validation set thats separate from training/test sets)

• disadvantage- less data

-alternatively use MDL / statistic estimates to decide whether to simplify

classifier performance

how constructed classifier performs at classifying new examples

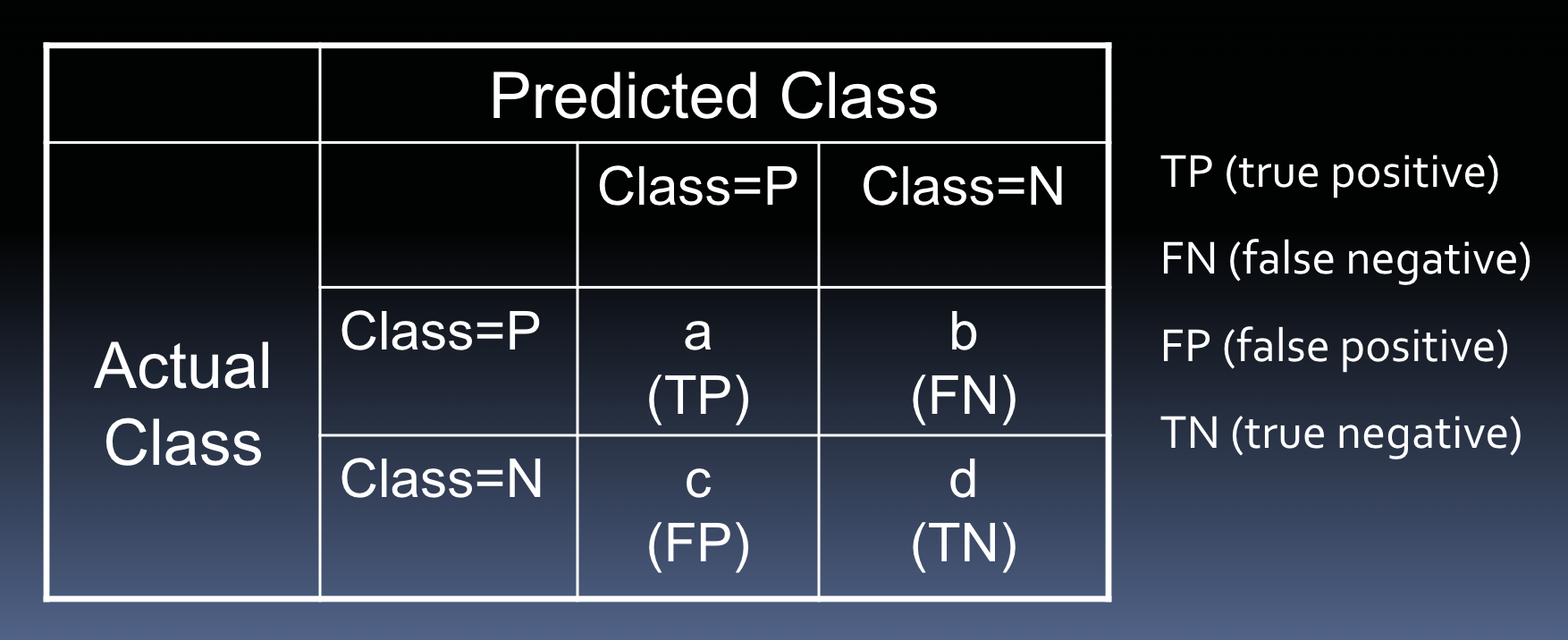
confusion matrix

-provides detailed results

-can be used to generate many metrics

-for k class problem → k x k matrix

accuracy and error rate

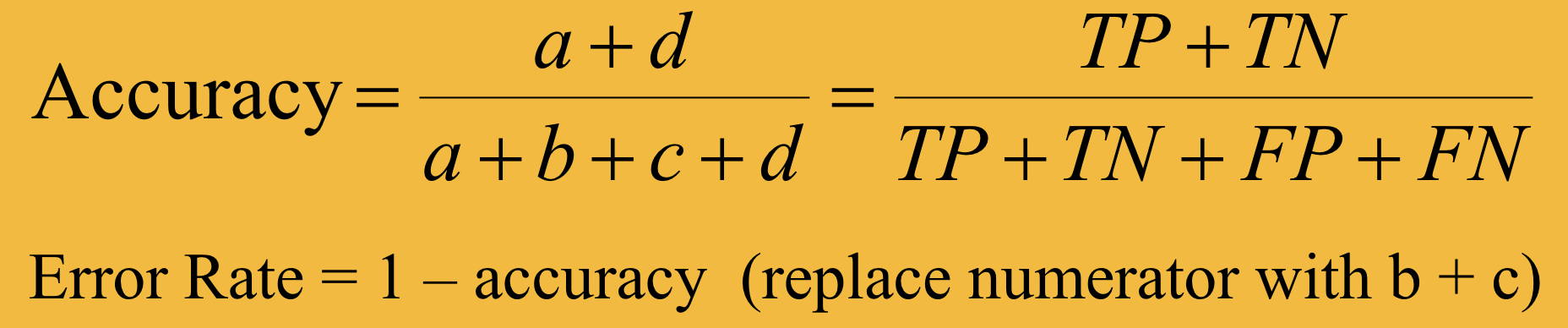
accuracy not that useful when

classes = imbalanced

ie. 9990 neg class examples and 10 pos → if model always predicts neg, accuracy is 9990/1000=99.9%

minority class often more important because

costs more to misclassify minority (positive)

ie. medical diagnosis- FN worse than FP

precision, recall, f-measure

-useful when class imbalance

-precision- accuracy when predict pos

-recall- fraction of pos you ‘catch’ (predict right)

-pos class = primary interest

-tradeoff b/n precision and recall

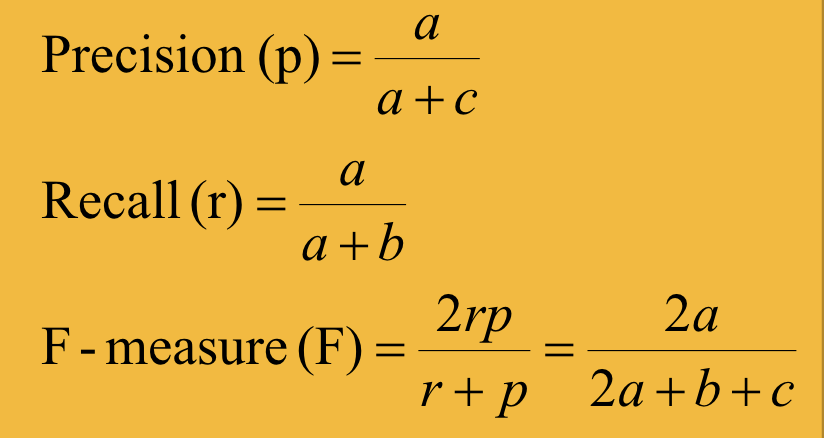
cross validation (xVal)

-partition data into k disjoint subsets

-train on k-1 partitions, test on remaining 1

• iterate k times so every ex is 1 of test sets

-most common is 10 fold xVal

-3-fold xVal in ex) 3 iterations, 2/3 train, 1/3 test each iteration; report performance over all k(3) runs

leave-one-out xVal

if n labeled ex, perform n-fold xVal

ie. if 1000 ex then use 1000 iterations each with 999 training and 1 test ex

why use xVal?

1. better use of data for training the model

   • uses more data for training → more accurate

   • tests on every ex → more reliable

2. multiple estimates = better reliability

   • individual estimates form a distribution

   • can use distributions to determine if 1 model better than another (t-test)

xVal disadvantage

extra computation

why do you need a validation set?

-training and test sets = not always sufficient

-problem when generating many models → parameter tuning / diff algs

• model w best test set performance may not be best because- only an estimate, small diffs may be due to chance → multiple comparisons problem

multiple comparisons problem

-random guessing → expect atleast 1 analyst to get results much better than random

-using test data to choose model instead of to build it

fixing multiple comparisons

use another data set to pick ‘best model’ → validation set (just like another test set but only used to pick best model)

using validation set process

-build multiple models w training data

-use validation set to decide best

-evaluate best model on test set and report

hyper-parameters

parameters that control the classification alg

ie. for DTs- splitting criteria, max depth, etc

validation set needed to choose

hyperparameter values

xVal can handle 3 partitions

-split data to training and test sets

-training set forms training and validation sets → build multiple models and pick best parameter

-choose model w best and evaluate test set

expressiveness

relates to flexibility and complexity of decision boundaries

for DTs all boundaries are axi-parallel which

somewhat limits expressive power

• most other classifiers more expressive (exception- linear classifier normally limited to 1 line/plane but not limited to axis parallel)

😔

computational efficiency

1. time to build DT

   • exponentially large search space → greedy heuristics allow quick construction

   • pruning = more time than build but still quick

2. time to classify a test ex

   • given a model → ex classified very quick

   • modest # of comparisons (most trees less than 10 levels)

-overall DTs very fast to build + apply

😄

explainability and comprehensibility

1. DTs very explainable

   • can explain/justify individual classifications (follow path to lead and examine splits)

2. DTs generate comprehensible global model

   • overview of entire model and how it works

   • diff from justifying individual decisions (nearest neighbor is explainable but no global model)

😄

applicability

1. no prior assumptions about data → no need to apply transformations to features 😄

2. handles discrete/continuous features → not ideal if many continuous features 😄

3. can natively handle >2 classes (multiclass) → linear regression and SVM natively handle 2 😄

4. doesn’t normally handle regression tasks → variants like CART via regression trees; an idea is to avg numerical class values at a leaf 😔

feature issues

1. handling missing feature values

   • not required to impute missing value to func

   • can treat missing values as special value → diff from numerical methods that build global func that requires each feature to have value

2. handling irrelevant/redundant features

   • good at this bc feature selection methods

   • irrelevance- ignored

   • redundancy- only 1 used in path to leaf

   • other methods like nearest neighbor have big problems

😁

data fragmentation

1. # of ex smaller as go down tree

   • at some point=too few to make statistically valid decision

2. worse when more features, fewer ex

3. not all methods susceptible to this (methods that dont use divide and conquer)- linear regression only uses 1 line so divides once

😔

data fragmentation problem happens since

keep partitioning data in DT

deterministic vs probabilistic classifiers

1. probabilistic- produces a probability for each possible class (sums to 1.0)

2. DTs are deterministic but produce probabilities as side effect (ratio of classes at leaf)

global vs local model

1. global- fits a single model to entire dataset

   • less susceptible to overfitting

   • linear classifiers considered global

2. local- partitions input space into smaller regions and fits a model to ex in each region

   • DTs considered local