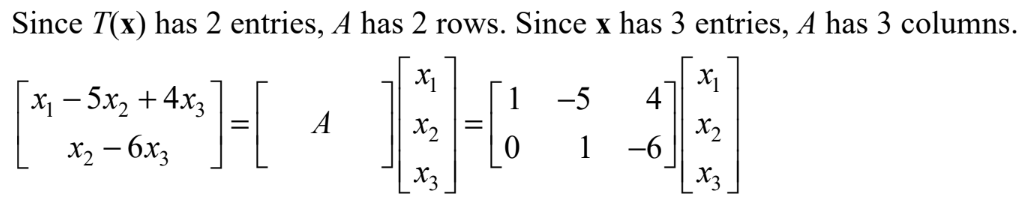MATH 3A Midterm Theorems

Each matrix is row equivalent to ________

one and only one reduced echelon form

Existence and Uniqueness Theorem

Inconsistent (no solution) if there is a row like [ 0 0 0 | b ] because b ≠ 0

Consistent (either one solution or ∞ solutions) otherwise.

• One solution: no free variables, all variables are leading

• Infinite solutions: at least one free variable

Matrix Equation Ax = b Theorem

If A has a pivot position in every row:

• Ax = b has a solution for every b in R^m

• Every b in R^m is a linear combination of a₁ … a_n (column vectors)

• Columns of A span R^m

Homogeneous Equation Theorem

Homogeneous equation Ax = 0 only has a nontrivial solution if there is at least one free variable

If Ax = b is consistent and let p be one particular solution then…

the set of all solutions is w = p + span (v1 .. vp)

We write w = p + v _h where v _h is any solution of Ax = 0

A set of vectors is called to be linearly independent if…

x₁a₁ + x₂a₂ … x_na_n = 0 has only the trivial solution

Has no FV

A set of vectors is called to be linearly dependent if…

If x₁a₁ + x₂a₂ … x_na_n = 0 has nontrivial solutions

If at least one of the vectors is a multiple of the other

If there is a zero vector

If there are more vectors than entries in the vector (more columns than rows, means there will be at least one FV)

Summary of trivial vs non trivial

No FV = linearly independent = trivial solutions = no zero vector

At least one FV = linearly dependent = nontrivial solutions = zero vector

A transformation is linear if

T(u+v) = T(u) + T(v)

T(cu) = cT(u)

Properties of linear transformations

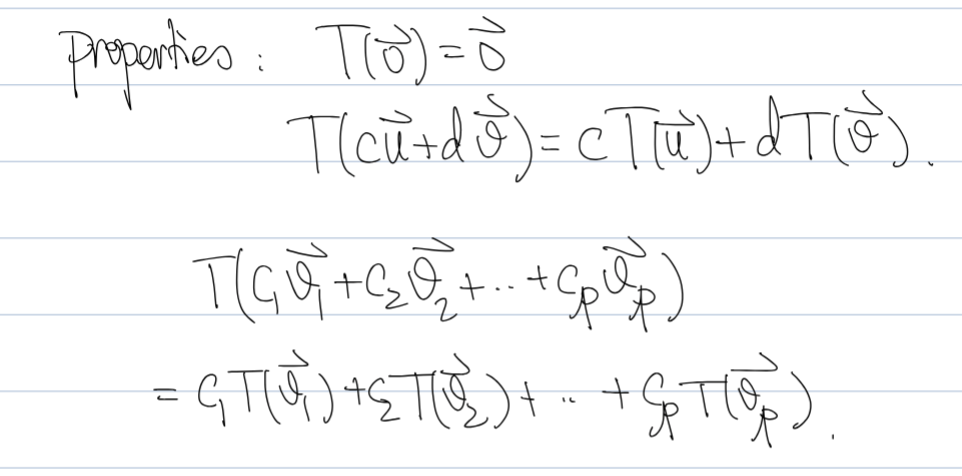
Let T: Rⁿ to R^m be a linear transformation. Then…

T: Rⁿ to R^m is said to be onto if…

Each b in R^m is the image of at least one x in Rⁿ

OR or every b in R^m, T(x) = b has at least one solution (consistent)

OR the range/span of T is the whole R^m

OR each row has a pivot

T: Rⁿ to R^m is said to be one-to-one if…

each b in R^m is the image of at most one x in Rⁿ

OR it has at most one solution

OR if each column has a pivot (no free variables)

OR T(x) = has only the trivial solution Ax = 0

OR columns are linearly independent

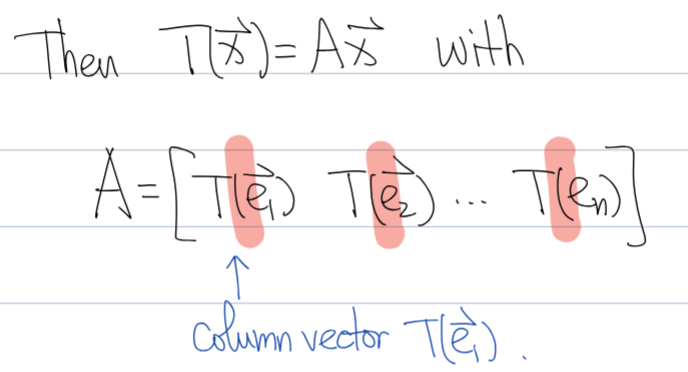
Let A be the standard matrix of T

T(x) = b => Ax = b has at least one solution for every b

All of these statements are true

Every b in Rⁿ is a linear combination of columns b = x₁a₁ + x₂a₂ … x_na_n

Span {a_1, a_{2 …}a_n} = Rⁿ

Ax = b is consistent

Each row of A has a pivot

Let A be the standard matrix of T

T(x) = b => Ax = b has at most one solution for every b

All of these statements are true

For b = 0, T(x) = Ax = 0 has only trivial solution

0 = x₁a₁ + x₂a₂ … x_na_n has only trivial solution x₁ = x₂ = … = x_n = 0

{a_1, a_{2 …}a_n} is linearly independent

A has no free variables # pivots ≥ column numbers (no cap for free vars)

Determinant Theorem

If ad - bc ≠ 0 then A is invertible

If ad - bc = 0, then A is singular

det(A) = ad - bc

If A is an invertible n x n matrix, then for each b in Rⁿ…

Ax = b has the unique solution x = A^-1b

Properties of Inverses

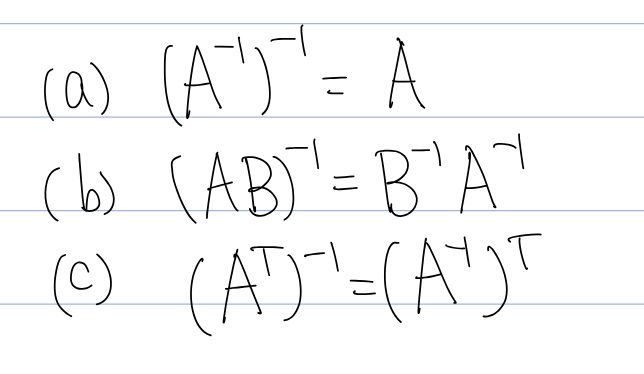
Characterization of Invertible Matrices

**only for the square matrices

From a row reduction perspective

• A is invertible

• A is row equivalent to the n x n identity matrix

• A has n pivot position

Once we know each column has a pivot

• The homogenous system Ax = 0 only has trivial solution x = 0

• The columns of A are linearly independent

• The linear transformation x |—> Ax is one-to-one

Meanwhile, each row has a pivot (consistent)

• The equation Ax = b has at least one solution for each b in Rⁿ

• The columns of A span Rⁿ

• The linear transformation x |—> is onto

From the matrix multiplication perspective

• There is a matrix such that CA = I

• There is a matrix D such that AD = I

• A^T is invertible

A linear transformation T: Rⁿ to R^m is said to be invertible if…

There exists an S: Rⁿ to R^m such that SºT(x) = S(T(x)) = x for all x and vice versa. S is the inverse of T

What is the standard matrix of T^-1

A^-1

A subspace of Rⁿ says H is in Rn if

0 is in H

For each u,v in H, u +v is in H

For each u in H, cu is in H

The column space of a matrix A is…

the span of all column of A

A is m x n A = [a1…an]

n column vectors in R^m

col A = span {a1..an} subspace of R^m

The null space of matrix A is…

the set of solutions to the homogeneous equation Ax = 0

Null space theorem

The null space of an m x n matrix is a subspace of Rⁿ

The basis of a subspace H is…

a linearly independent set in H that spans H

The basis for Col A

The pivot columns of a matrix A

The dimension of H

Denoted by dim H = the number of vectors in any basis for H

Rank of Matrix A

Denoted by rank A = dim col A
# of pivot columns in its reduced echelon form

Rank Theorem

A is m x n

Rank A + dim Nul A = n

#pivots + #free variables = total number of variables

Basis Theorem

If dim H = p, then any p linearly independent vectors of H automatically form a basis of H

If A is n x n then the following is true

A is invertible

col A = Rⁿ

rank A = n

dim Nul A = 0

Nul A = {0}

What are a and b when there is a transformation from R^a to R^b

a = # columns

b = # rows

Remember this