Exam 2

mode

the value of the most common score of the variable

the only and best measure for nominal variables

median

the middle value in a frequency distribution

could be used for ordinal, interval, and ratio scales

best when the shape of the distribution for the interval/ratio variable is skewed

mean

average

best for interval and ratio scales

best when the shape of the distribution for the interval/ratio variable is symmetrical and unimodal

how skewed distribution affect each measure of central tendency

mean: in a right-skewed distribution, the mean is higher than the median and in a left-skewed distribution the mean is lower than the median

median: the median remains a better measure of central tendency in skewed distributions because it is less affected by extreme values

mode: the mode indicates the most frequent value, which can remain unchanged regardless of skewness, but its position relative to the mean and median can indicate the direction of the skew

how outliers affect each measure of central tendency

mean: outliers can pull the mean up or down, making it unrepresentative of the main data

median: the median is less affected by outliers as it is the middle value, so it stays closer to the center of the main data

mode: the mode, being the most common value, is not affected by outliers unless they change what is most frequent

how does measurement scale affect the measure of central tendency you use

the type of data you have decides which average to use

for nominal data, you should use the mode

for ordinal data, you should use the median

for interval or ratio you usually use the mean if it's balanced or the median if it's skewed

what are we describing with the measures of variability

measures of variability tell us how much the numbers in a set are spread out

show how different the values are from the average

most common: range, inter-quartile range, variance, and standard deviation

absolute range

the difference between the smallest and largest observed value

pros:

cons: does not consider distribution shape, highly susceptible to outliers

inter-quartile range

the range of the middle 50% of values, between the 25th and 75th percentile

pros: tells you how variable the observation in the middle of the distribution is without being affected by outliers skewed distributions

cons:

anatomy of box-and-whisker plots

graph the median with IQR and range, which visualizes central tendency and variability together

pros: helpful for comparing distributions

cons:

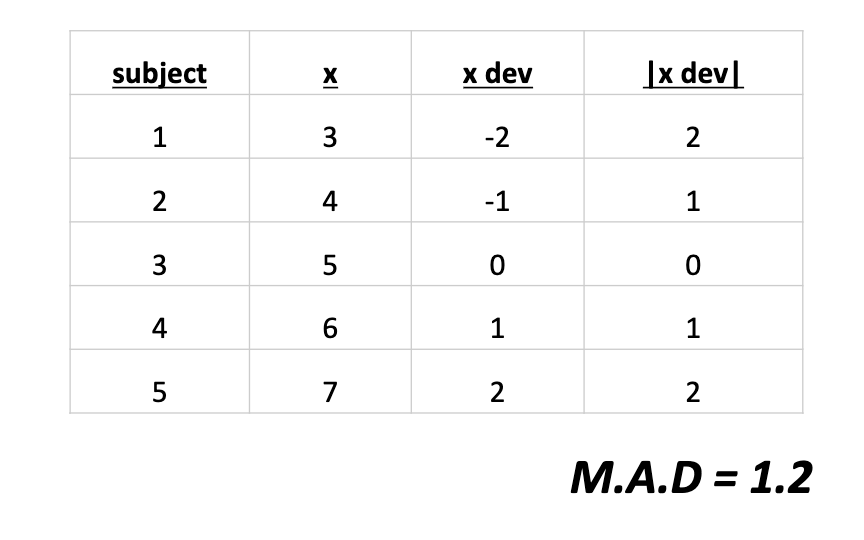
mean absolute deviation

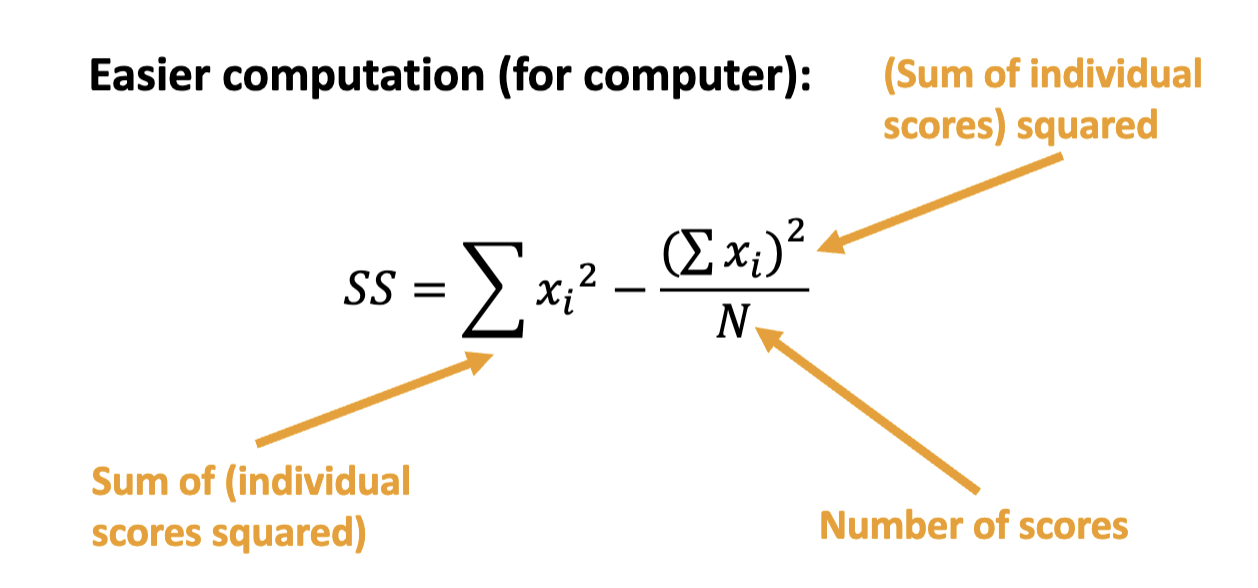
sum of squares

variance

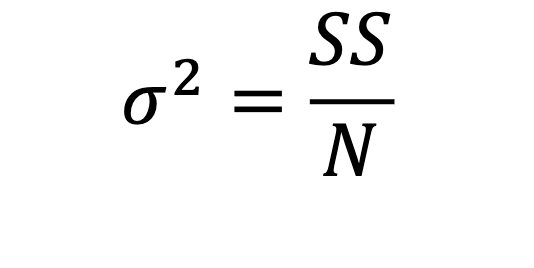
standard deviation

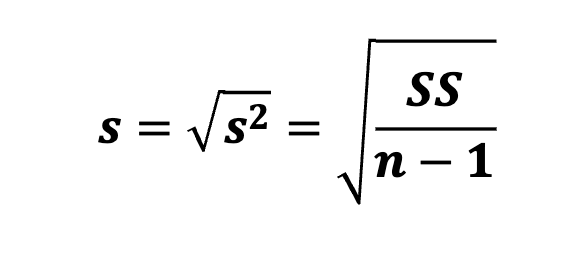
how do outliers and skew affect which measure of variability is used to detect outliers

outliers can distort measures like the range and standard deviation.

when the data is skewed, the inter-quartile range (IQR) is better for identifying outliers because it focuses on the middle 50% of the data and is less influenced by extreme values

degrees of freedom

degrees of freedom refer to the number of independent values or quantities which can be assigned to a statistical distribution

calculated as the sample size minus the number of parameters estimated from the data

how a z score is computed

how to interpret a z score in terms of units of standard deviations

a z score indicates how many standard deviations a data point is from the mean

a z score of +2 means the data point is two standard deviations above the mean

a z score of -1.5 means it is one and a half standard deviations below the mean

what does a z score of zero reflect

a z score of zero reflects that a data point is exactly at the mean of the distribution

indicates no deviation from the average value of the dataset

how can z scores compare variables measured with different units

they can be compared directly or used to compute an average "composite score”

how can z scores identify outliers based on a criteria of standard deviation

use benchmark of standard deviation to determine whether a score is an outlier

what kind of claim do we use the Pearson r for

association claims

what are the expectations for the data when using the Pearson r

the relationship must be linear

anatomy of the Pearson r equation

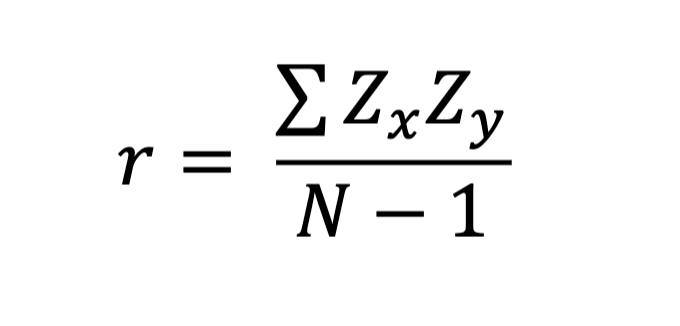
how does the Pearson r indicate strength and direction in the statistic

the strength is -1 to 1 range

the direction is +/-

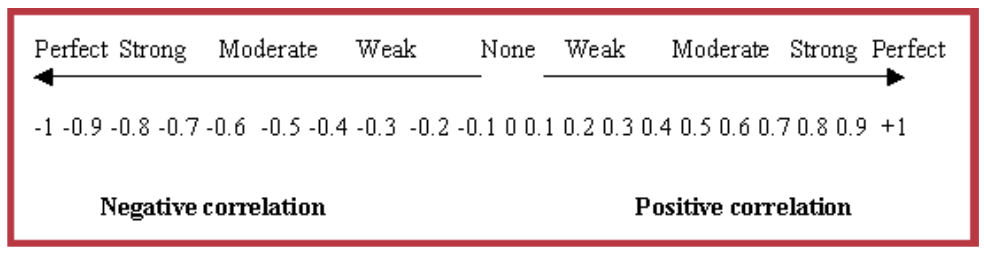
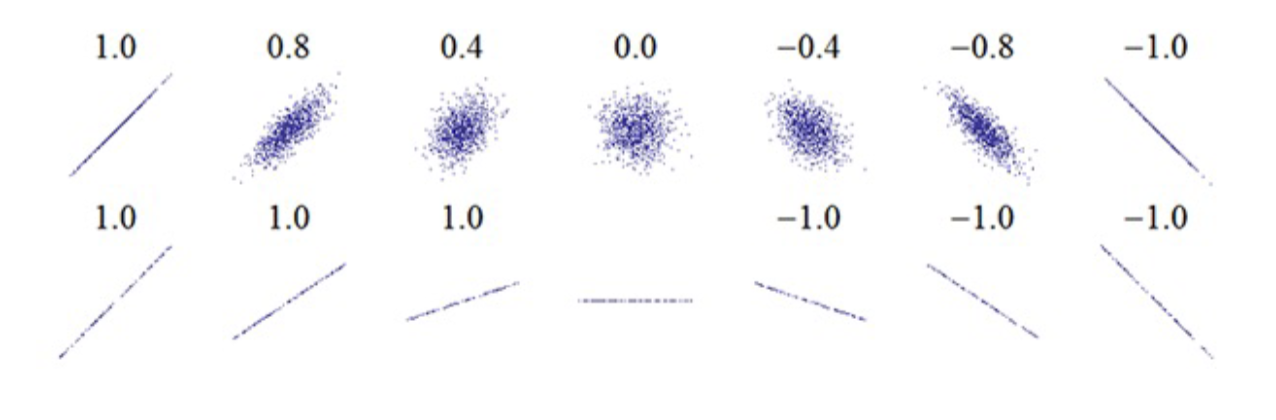
how does the Pearson r indicate strength and direction in the scatter plot

the strength is estimated by how close the points are to a trendline

direction is shown by the slope

impact of different kinds of extreme scores when interpreting the Pearson r

positive extreme scores can inflate the correlation, suggesting a stronger relationship than there actually is

negative extreme scores can deflate it, masking a genuine relationship.

range restriction when interpreting the Pearson r

-1 to 1

describing your result in words when interpreting the Pearson r

what is descriptive statistics

“unitless”

effect size for the strength of the relationship

effect sizes are comparable across different variables and studies

difference between sample statistics and population parameters

sample statistics summarizes the sample of the study (known)

population parameters summarizes the entire population (unknown)

what are the distinct goals of descriptive and inferential statistics

descriptive statistics aim to summarize and describe the characteristics of a dataset, providing an overview of its main features

inferential statistics focus on making predictions or inferences about a population based on a sample, assessing relationships and testing hypotheses

estimation vs. precision

estimation is a single estimate of a population value based on data from a sample

precision is refining statistics by using larger sample sizes and lowering variability

what is a 95% confidence interval, and how does it help us make an inference about a result

a range of how precise our point estimate is by capturing a range that very often contains the true population value

a 95% confidence interval that contains the population value 95% of the time

it helps us make an inference about a result by making a range of realistic values

how to interpret confidence intervals for Pearson correlations

confidence intervals for Pearson correlations provide a range within which the true correlation coefficient is likely to lie

what is null hypothesis significance testing (NHST)

an inferential statistical technique in which a result is compared to a hypothetical population in which there is no relationship or no difference

how are p-values used for interference with this approach

in NHST, the probability of getting the result in a sample or one more extreme, by chance, if there is no relationship or difference in the population

what is an alpha criterion

researchers decide whether the p value obtained from a sample statistic is low enough to reject the null hypothesis or too high, and thus retain the null hypothesis