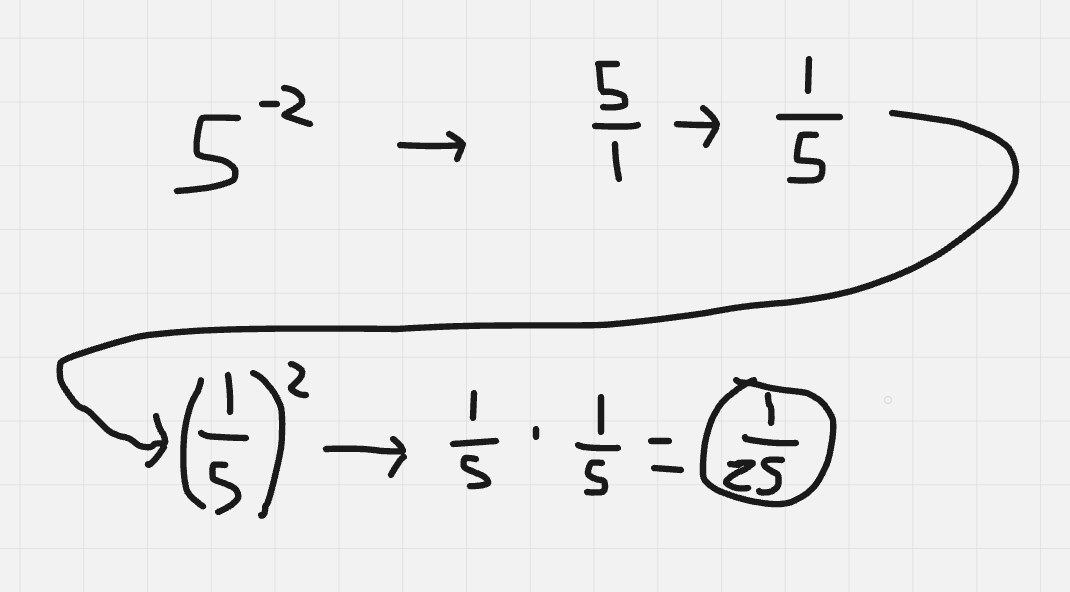inverse functions

Normal function vs inverse function appearance

What is a one to one function?

A function that has no two X values that can have the same Y value

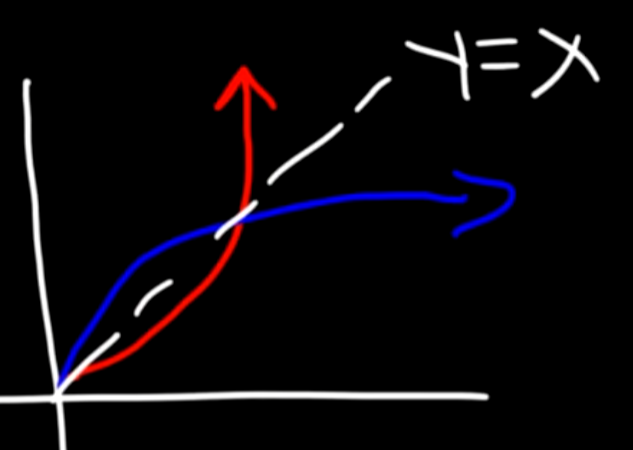
What is the line of symmetry for inverse functions and what does it look like?

The dotted line is y=x

Inverse function differences from normal function

Inverse function has opposite domain and range from normal function, and the x and y coordinates are flipped for each ordered pair.

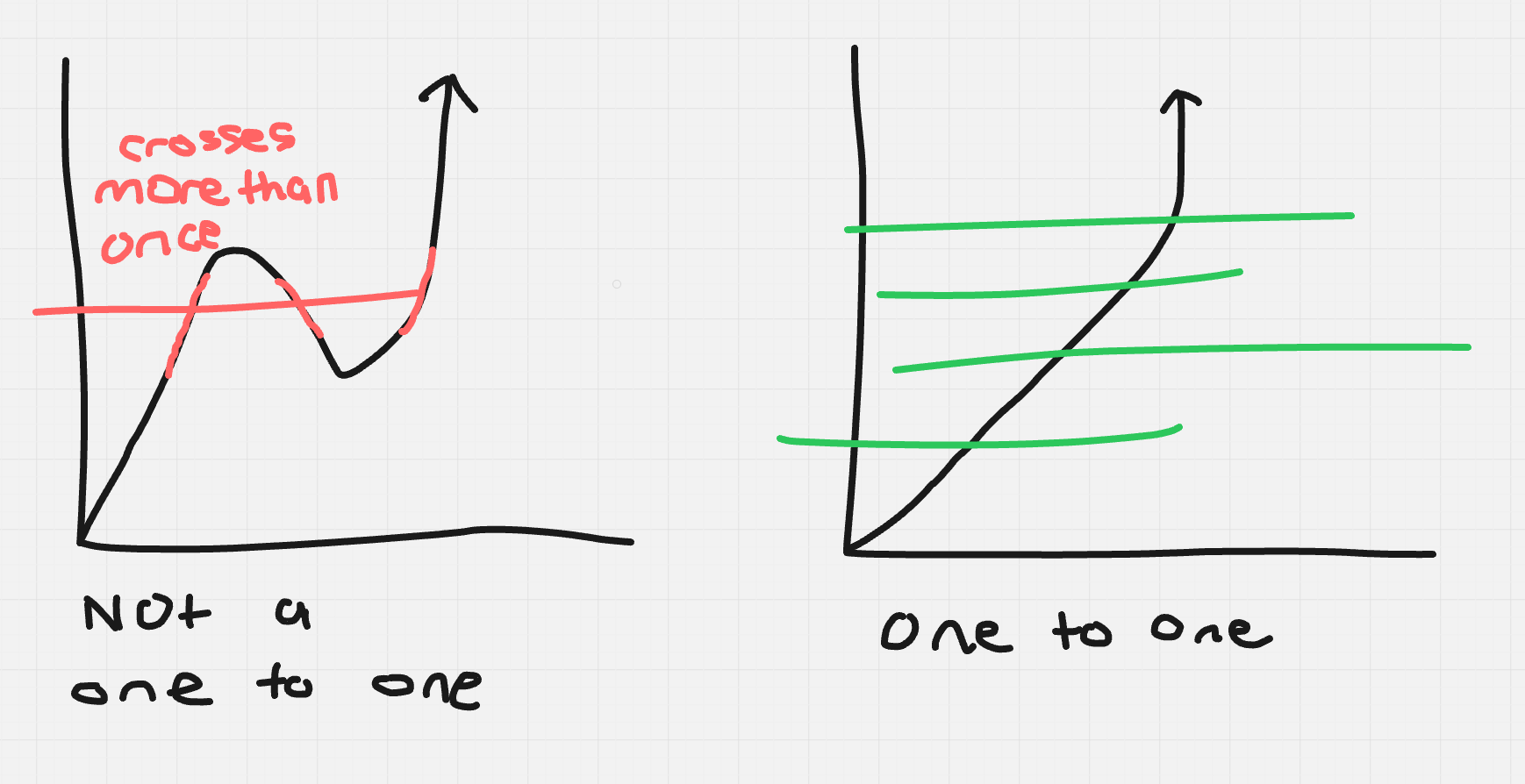
What is the difference between the horizontal and vertical line test?

How is it passed, and is it passed in the same way regarding how many times a line can go over a function/relation

The vertical line test is meant to tell if a relation is a function

The horizontal line test is meant to tell if a function is a one to one function

.

They are both passed in the same way, by making sure a line (whether horizontal or vertical) doesn’t ever overlap with the function more than once

For each graph, which is a one to one and which is not?

What must a relation be, before you check if it’s a one to one function?

A function, so it must pass the vertical line test before you begin the horizontal line test or equation method to find out if its one to one

For each, determine if it’s a one to one function

How to tell if a function is one to one? (not in graph)

set f(x) as
f(a) = f(b)

a = b ; if it’s a one to one function

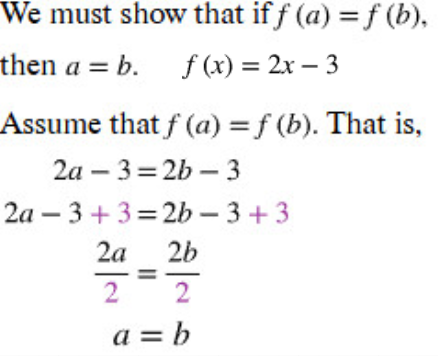
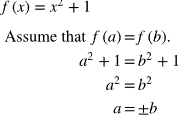
Is the plus or minus able to be considered equal to A? And is it considered one to one?

No because it includes minus, so the function is not one to one.

What formula(s) do you use when you are trying to tell whether 2 functions are inverses of each other

Both composite functions need to equate to X in order for the two functions to be inverse

What is the procedure/steps in order to find the inverse of a function?

Step 1: Replace the f(x)= to y=

Step 2: Swap the x and y from y= to x=, as well as swapping the other side as well. ex. y=2x to x=2y

Step 3: Solve for y, and keep/use the x in the equation as well. ex. y=x/2

Step 4: Swap the isolated y with the inverse function of x. ex. y=x/2 to f^-1(x) =x/2

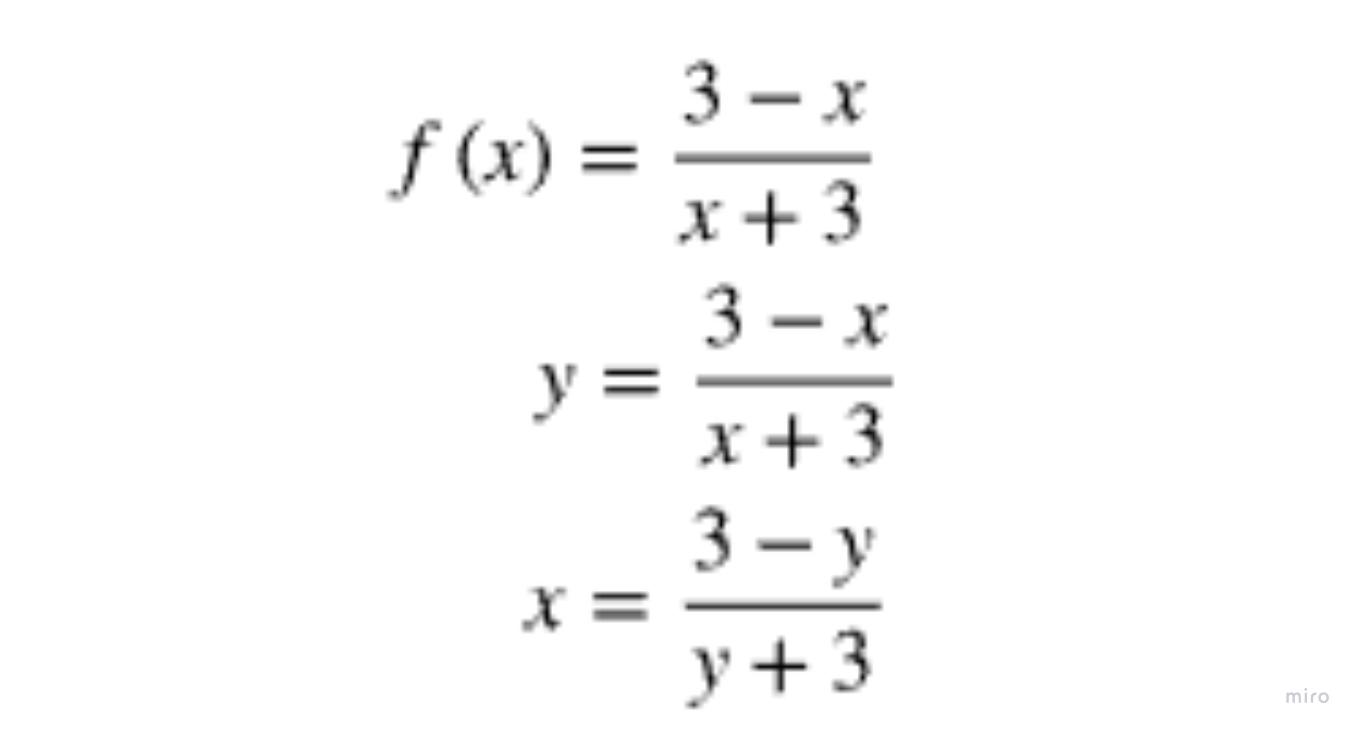
What is the next step in trying to find the inverse function?

You multiply the denominator on both sides to undo the fraction

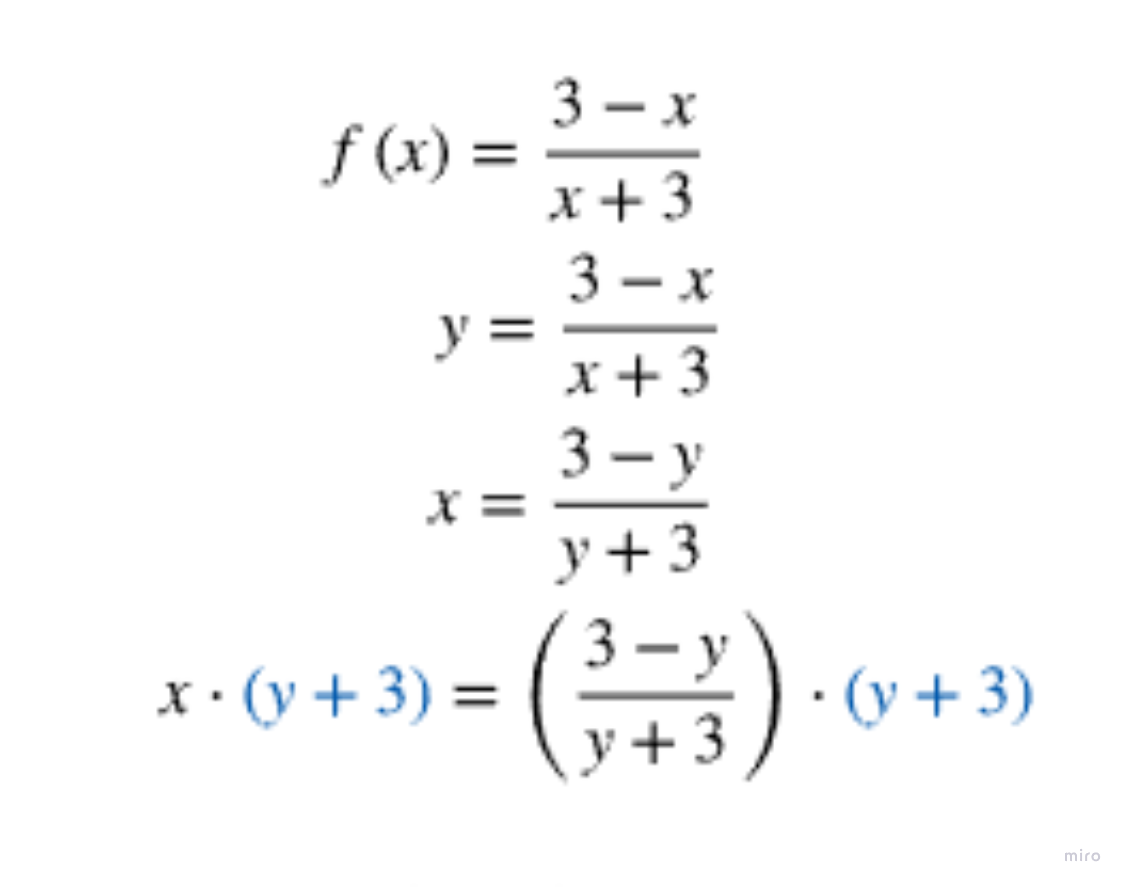
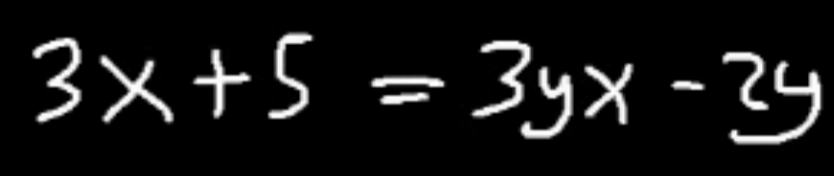
How do you isolate the y from this point

Factor out the y, then divide everything else on both sides

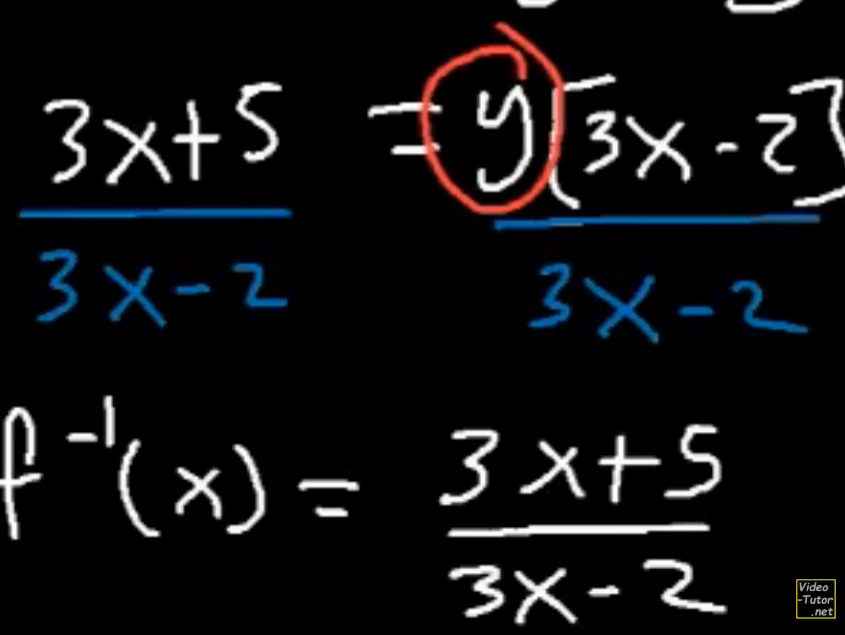
Does cube root have restriction?

No because the restriction to be greater than or equal to 0 in the radicand doesn’t apply, when an odd root doesn’t require the radicand inside to be positive, so it’s all real numbers

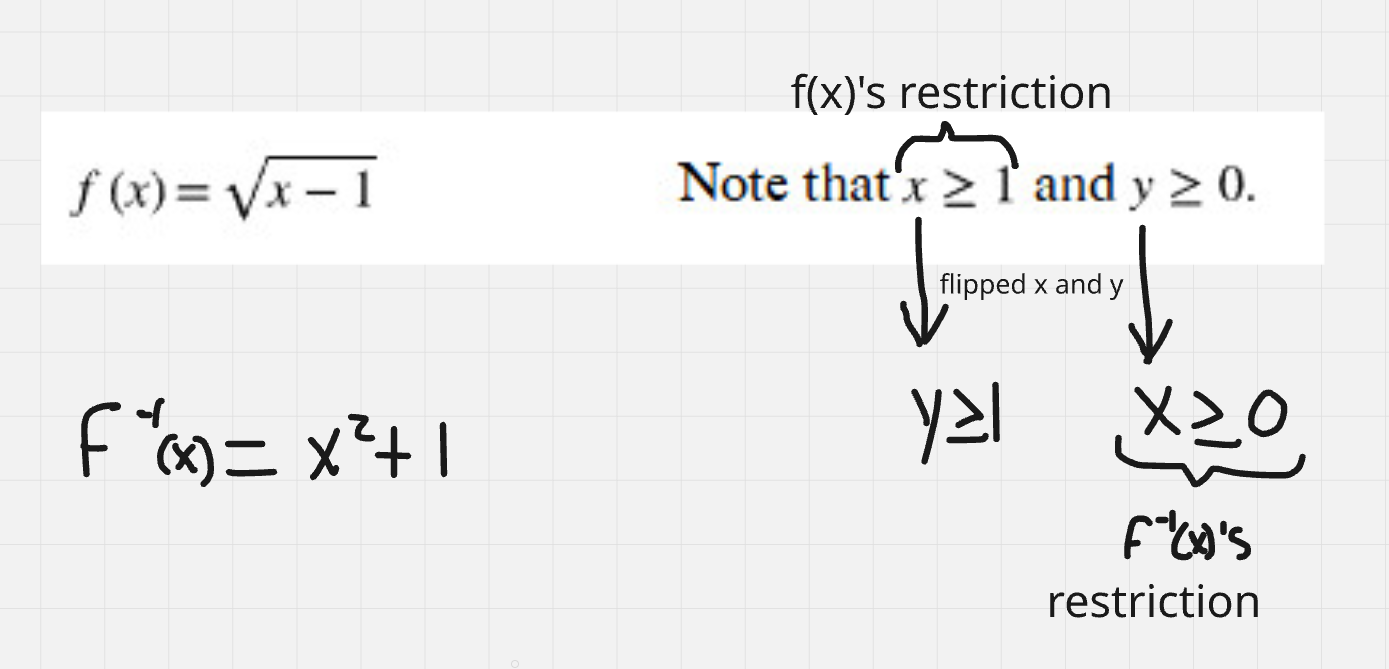
In an inverse function, do the restrictions of x and y flip from the normal function?

Yes since the domain and range are flipped

When a function has a radical restriction, does it still use a restriction in the inverse function? and if so, which one?

When a function has a radical restriction in the domain(ex.x>0), then the inverse function will also have a radical restriction in its new domain (the original function’s range).

Do you only include the domain(x) for restrictions in functions, even after rewriting as an inverse function?

Yes, even after a function has been rewritten as an inverse function, the x/domain will remain the only possible axis for restrictions to be applied on, although the inverse’s restriction domain will be the original function’s y/range

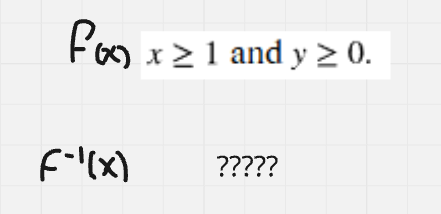
What is the inverse function’s domain and range (don’t write in interval notation)

Swap the x and y

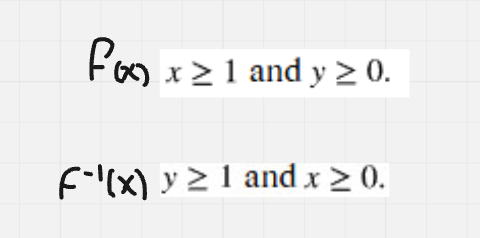
What would be the restriction for the inverse function?

x ≥ 0
since x and y get flipped in inverse function as well as domain and restrictions, and then you still use x/domain to represent the new restriction

For the inverse function, is it plus or minus in front of the radical, or something else?

Needs to be negative in front of radical due to function’s restriction affecting/becoming the new range for the inverse function.

It would have been positive if the inequality sign had been flipped so that x was greater than or equal to 0.

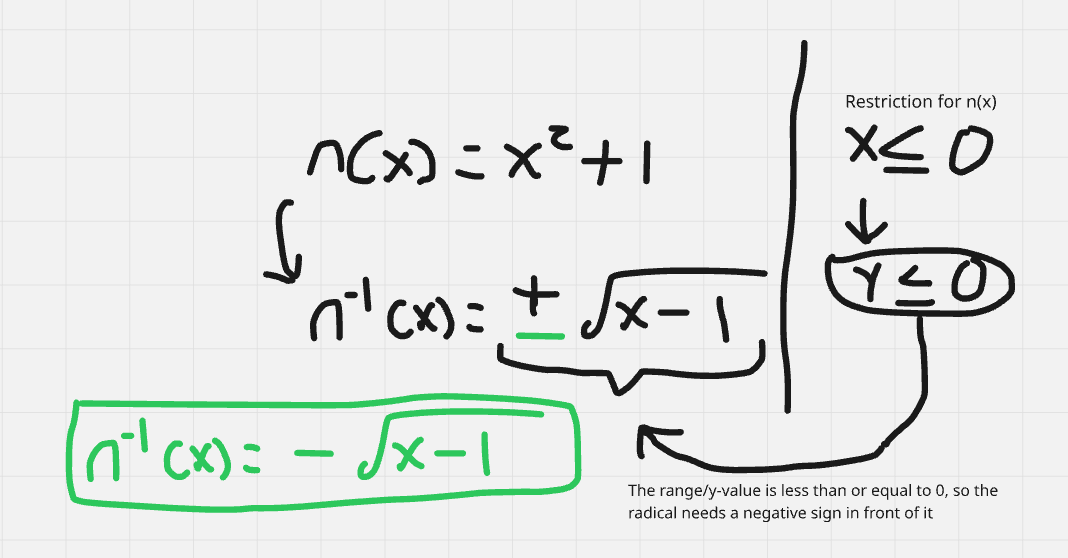
When you are already being given a restriction when asked to find the inverse of a function, what does that mean? And what do you do?

It means that you will be rewriting the function’s inverse as a radical, or will at least include a radical.

You will also have to turn that x into a y for the restriction, and in this case you use the y restriction to determine whether you use a plus, and a minus, because you are not using both if you have a y restriction now

You do not write the y restriction, rather you just use it to determine if you choose plus sign, or minus sign.

Negative exponent rule

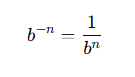
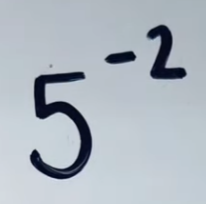
Simplify negative exponent

For negative exponents, find the reciprocal of the base (5), then square the reciprocal (1/5).

(1/5)² = 1/25