General Equilibrium and the Welfare Theorems

A pure exchange economy

• Aim to describe an economy through simple concepts

• We need three objects, a set of traders, preferences, and resources (each agent is given some endowment)

• Generally we’ll use the simple framework of two agents and two goods

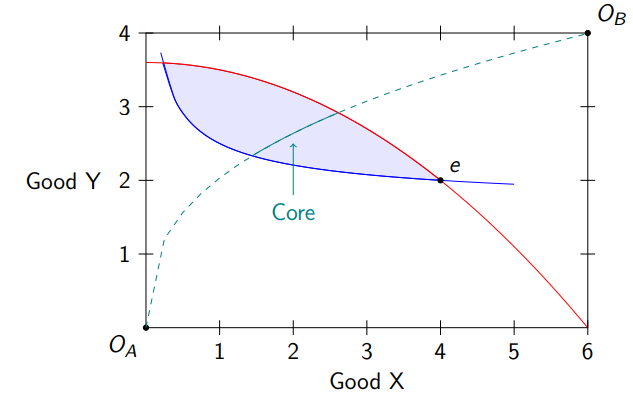
The Edgeworth Box

• Consists of fitting the different indifference curves of the different agents into the same graph, from opposite origins, where the sizes of the edges represent the total resources in the economy

• There are equilibrium trades where the indifference curves intersect

The contract curve

• Is on the same Edgeworth box as the other utility curves, and is the set of all possible Pareto efficient allocations 

• The set of Pareto efficient allocations which improve upon the original endowment is called the core 

Allocation in competitive markets 

• The main mechanism for allocation is price, meaning individuals simply maximise where their income is the value of their endowment (endowment is valued in monetary terms)

• A competitive equilibrium occurs when there is an allocation that maximises each person’s utility at a set of prices (they are price-takers) and the market clears 

• On the Edgeworth box, the difference between the original equilibrium and the competitive equilibrium can be conceived of in terms of an agents excess supply and excess demand 

What is the first fundamental theorem of welfare?

• Competitive equilibrium allocations are Pareto Efficient

• Requires some monotonicity of preferences as an assumption

• This tells us that a competitive economy will end up at some point on the contract curve; a lump sum transfer is a way of transferring money to change the initial endowment and end up on a better place on the contract curve

What is the second fundamental welfare theorem?

• For each allocation on the contract curve, there is a price that supports it as a competitive equilibrium 

• The results requires convexity of preferences and tells us what we can achieve with redistribution 

• Every point on the contract curve can be reached through decentralised trade

What are political implications of the welfare theorems?

• Markets can produce good results

• Perfectly competitive markets provide the benchmark

• Government redistribution can help ease ethical concern within the market

The second theorem and lump sum transfers

• The second theorem assumes we can do lump sum (costless and immediate) transfers (presumably done by the government through taxation)

• This taxation can still lead to an equilibrium market outcome so long as the thing being taxed can be measured or can’t be changed (taxing people with blue eyes’ endowment and giving it to people with brown eyes. Or, taking from people with High IQ’s endowment and redistributing it to lower IQ endowments)

  • This works because we recognise that all trades which occur from initial endowments will result in a Pareto efficient market equilibrium

Situations in which markets are inefficient

• Market power: there are agents big enough to be price-makers rather than price-takers

• Externalities, where one individuals welfare depends on the consumption of others 

• If information is incomplete, trading might be obstacled leading to inefficiency 

• The pricing of public goods by private sectors doesn’t result in efficient allocation 

What is gross demand?

• Gross demand is the total amount of a good that a person wants to consume at the going price

What is net demand?

• This is the difference between gross (total) demand and the initial endowment they already have

  • It is how much the consumer needs to buy of the good to satisfy their demand of the good

What is Walras’ Law?

• It is a condition which specifies that in equilibrium, the value of the aggregate excess demand in an economy is identically equal to 0

  • p₁z₁(p₁, p₂) + p₂z₂(p₁, p₂) = 0

• This identity means that the value of aggregate excess demand is necessarily 0 for all prices, not just those in equilibrium; it is stronger than necessary

Relative prices

• Walras’ law demonstrates that in a market with k goods, we only need to find prices for which k-1 markets are in equilibrium; the k^th market will necessarily be in equilibrium

• It seems that we are unable to solve for the final price because we have k goods and only k-1 equations, but this is because the k-1 equations are only solving for independent prices

• Thus we need to fix a price as constant so that all other prices can be measured relative to it

What is Arrows’ Impossibility Theorem?

• If a social mechanism satisfies certain properties (1. the decision mechanism should be complete, transitive, and reflexive, 2. everyone should rank x ahead of y if everybody prefers x to y and 3. that preferences between x and y should depend only on how people rank x versus y and not on other preferences) then this social decision-making mechanism is a dictatorship

  • This just means that this mechanism for choosing between pareto efficient outcomes resembles the preferences of just one person, not many

• If we want to aggregate social preferences whilst maintaining democracy, we will have to give up one of the three properties that are listed in Arrow’s impossibility theorem

When is an allocation equitable?

• An allocation is equitable when a person doesn’t prefer any bundle over their own allocation

• To desire another persons bundle is to envy it

• We say that if an allocation is equitable and pareto efficient, then it is a fair allocation