PSAD BASIC STRUC

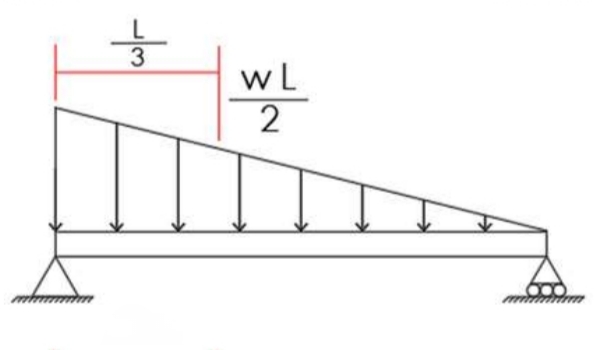
Triangular Load to Point Load and its location

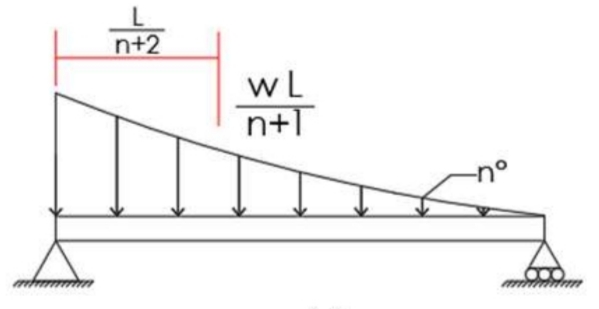
Spandrel Load to Point Load and its location

Forces with a common point of action

Forces that do not intersect

Forces that do not have a common point

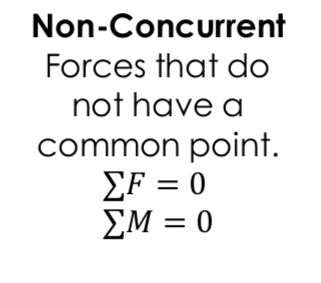
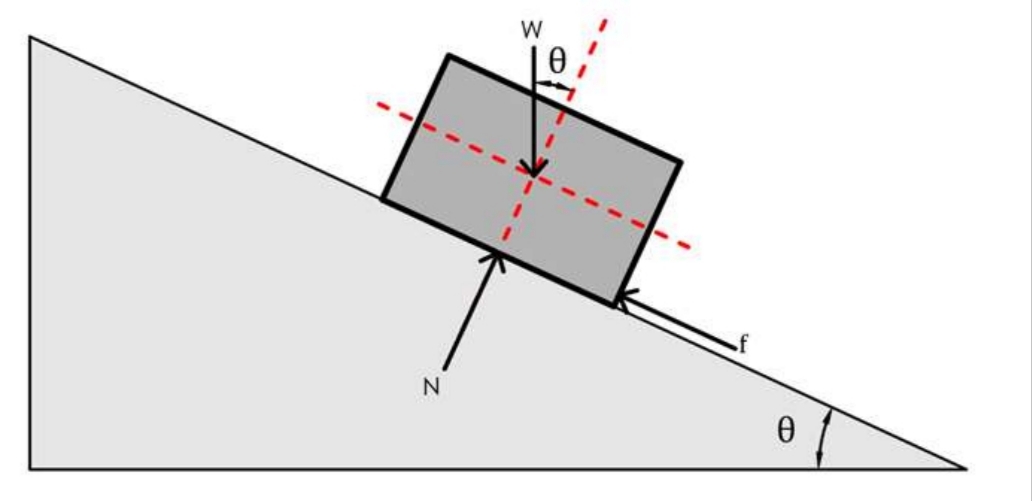
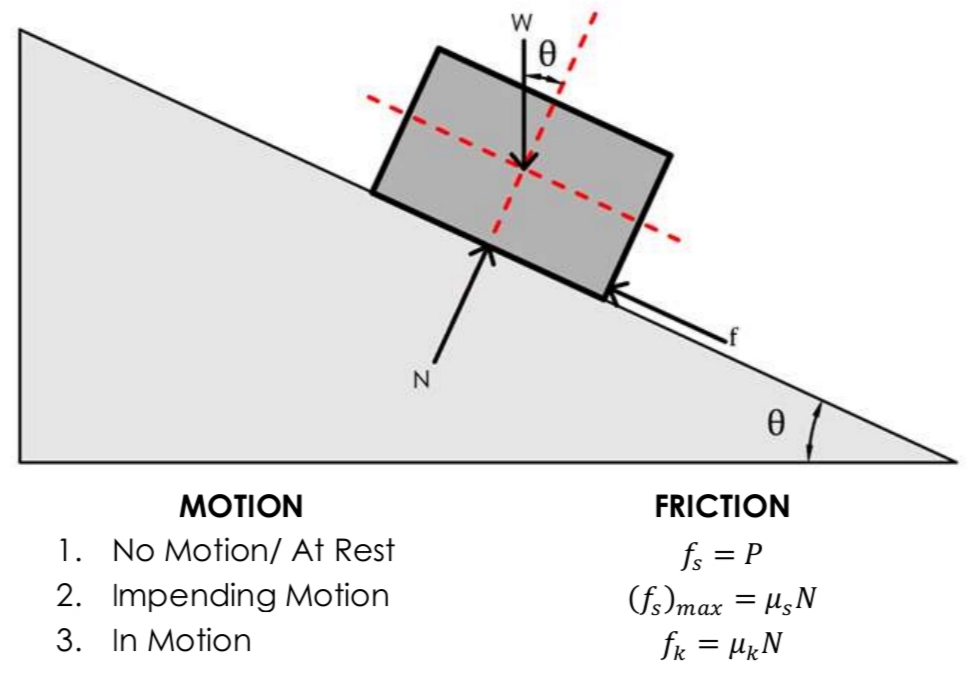
What is Friction in

1. No Motion/At rest

2. Impending Motion

3. In Motion

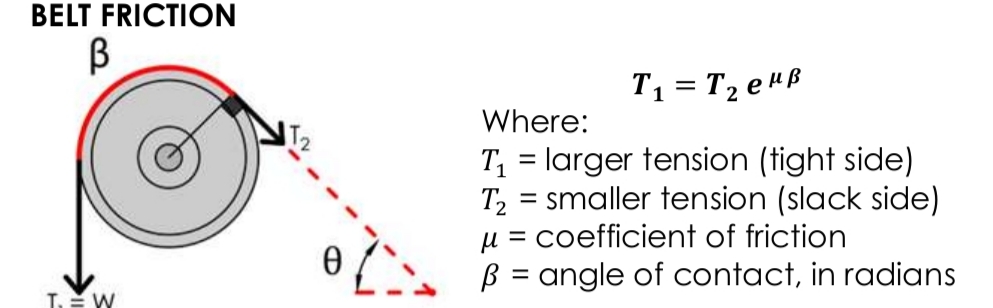
Belt Friction

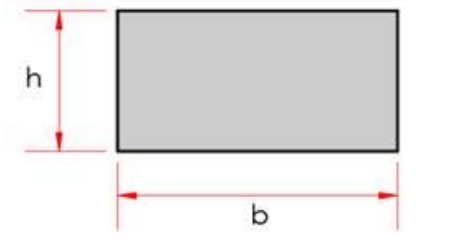
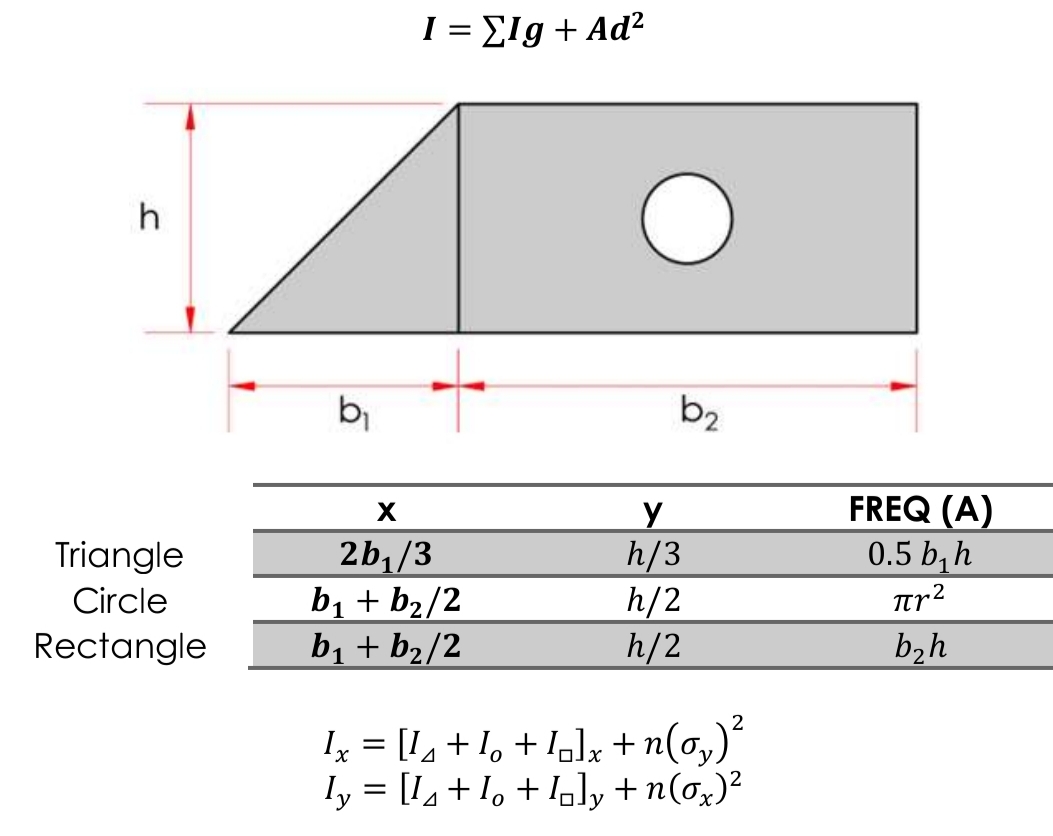
Moment of Inertia in Rectangles

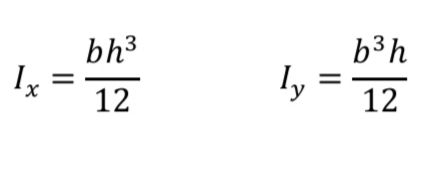
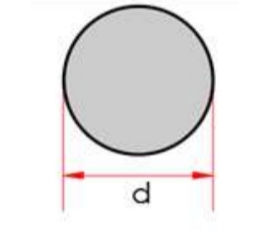
Moment of Inertia in Circles

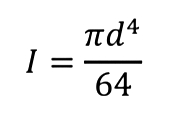
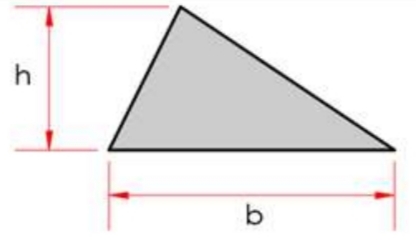
Moment of Inertia in Triangles

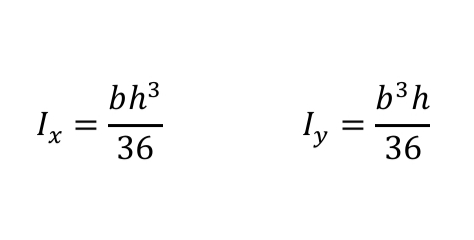
Parallel Axis Theorem

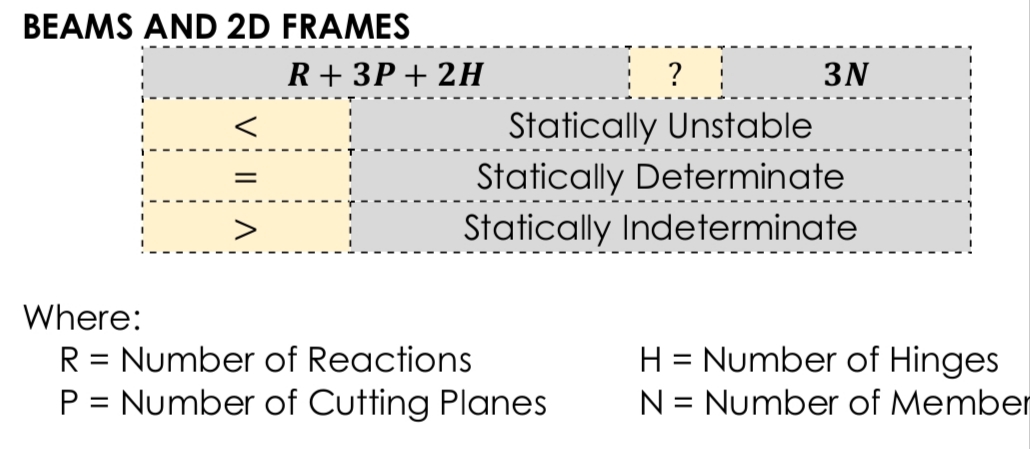
Stability and Determinacy (Beams and 2D Frames)

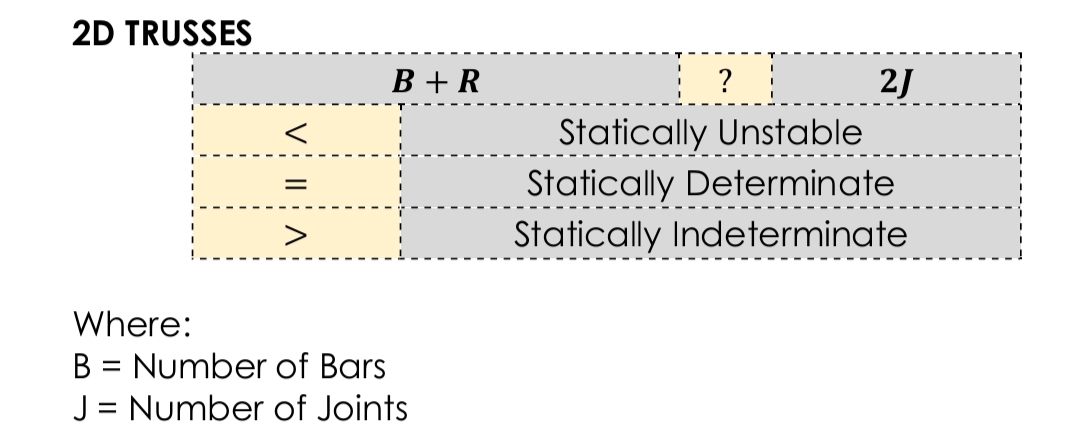
Stability and Determinacy of 2D Trusses

Degree of Indeterminacy

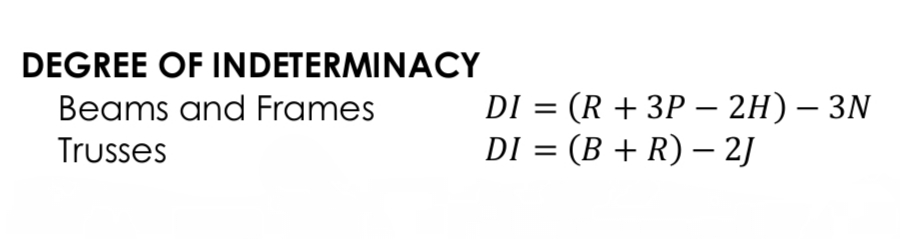
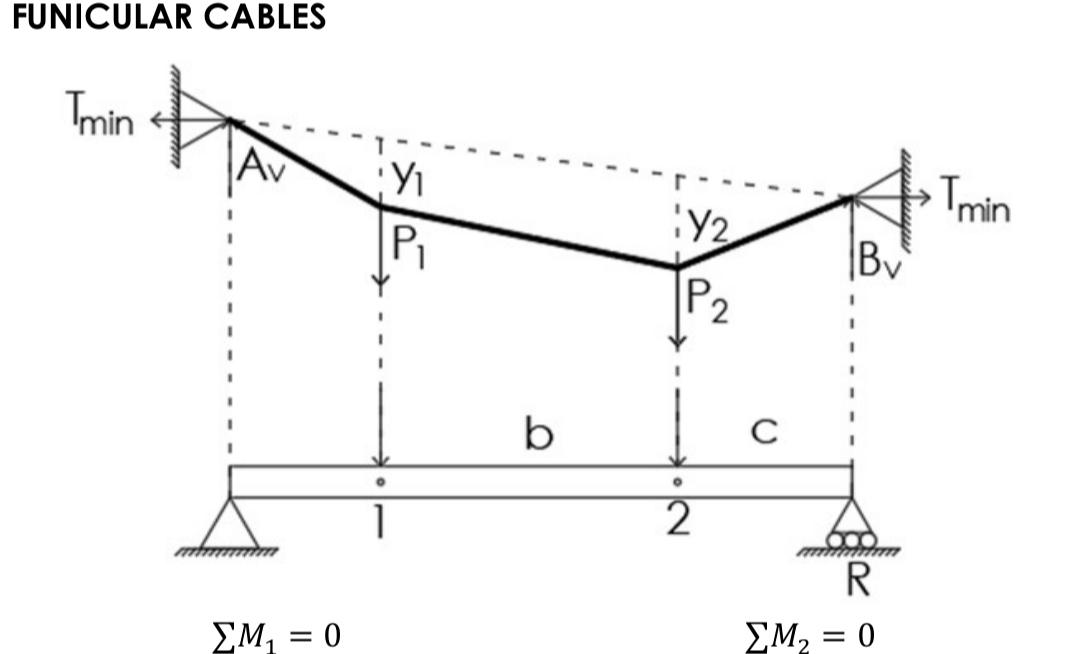
Funicular Cables

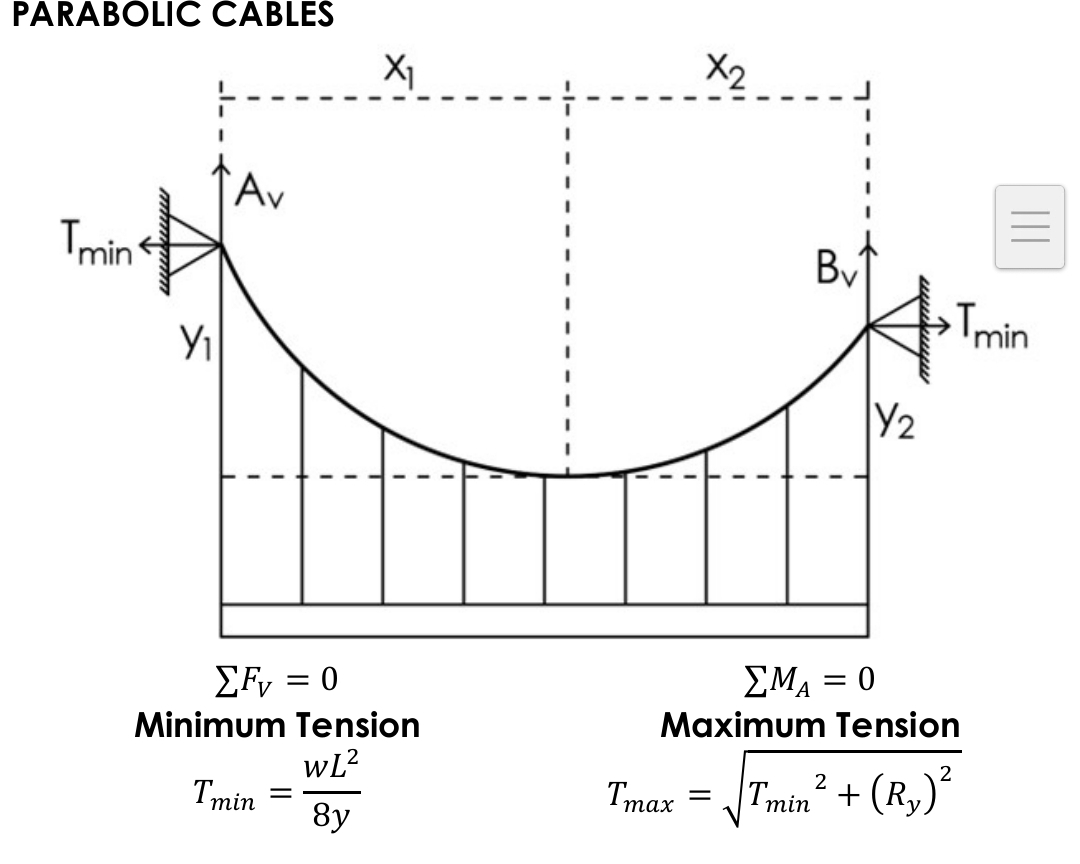
Parabolic Cables: How to get Minimum and Max tension and Length of Cable

1. Locate lowest point using SPP x²/y=x²/y

2. Cut in lowest part of cable, and moment at support to get Tmin

3. To get Tmax, Get resultant of Tmin and Vertical reaction of the highest support

4. To get length of cable: Caltech Mode3:3 and get the equation A+Bx+Cx². Integral of square root of 1 + (dy/dx)² from a to b.

Influence Line: Maximum Reaction (Diagram)

Influence Lines: Maximum Shear (Diagram)

Influence Lines: Maximum Moment

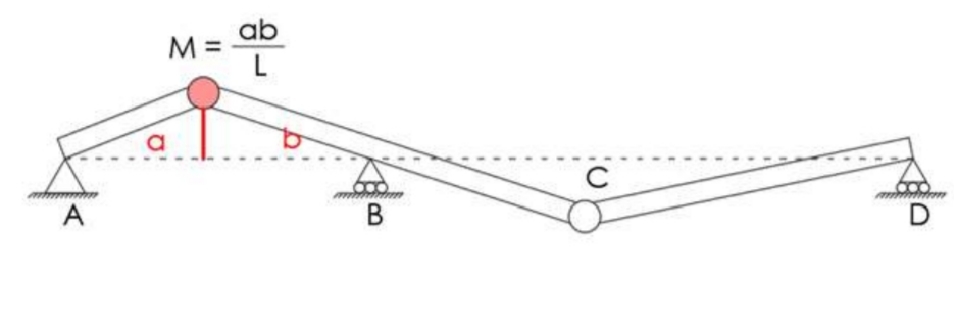
Influence Line: General Process

To get maximum values

1. Multiply Point load to highest Ordinate

2. Multiply Distributed Load to Area under line

3. Apply Dead Load throughout the beam

4. Apply Live load only to max positive or max negative area

Moving Loads: General Process for Maximum Shear

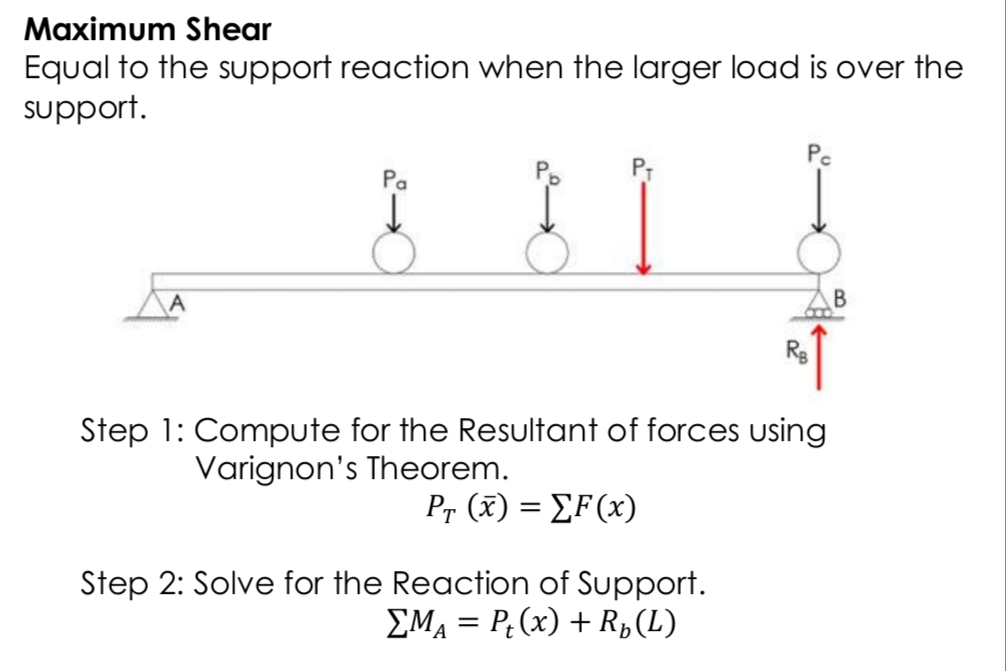
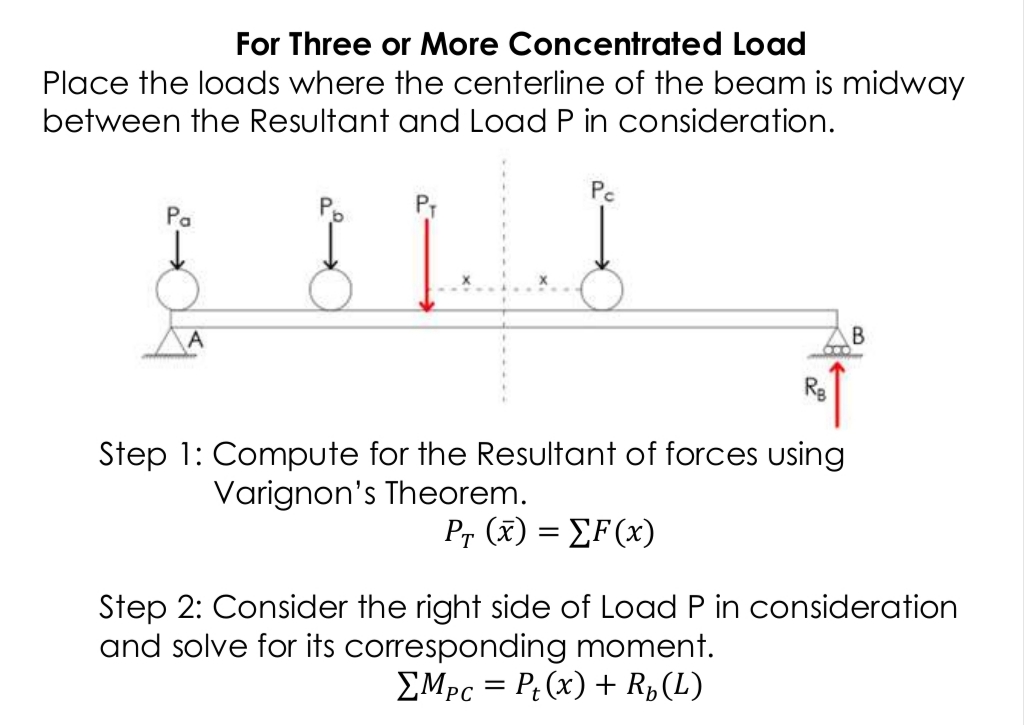
Moving Loads: Maximum Moment General Process for one and two Point Loads

Maximum Moment dor 3 or More Concentrated Load

Double Integration Method

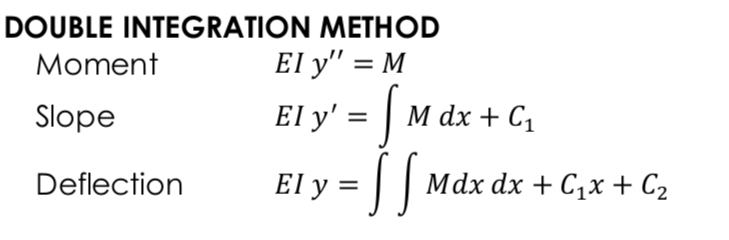
Area Moment Method

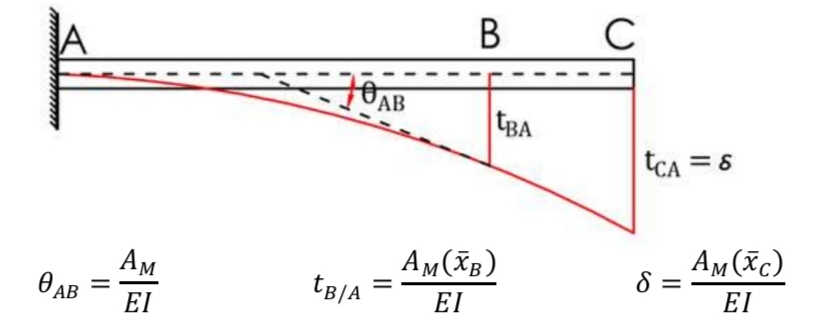
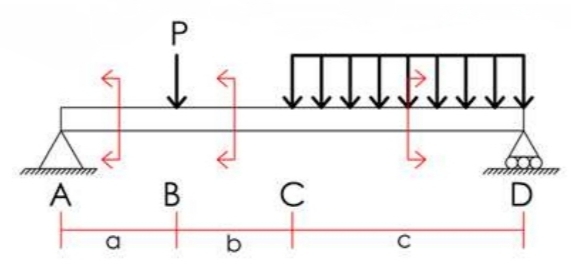
Virtual Work Method

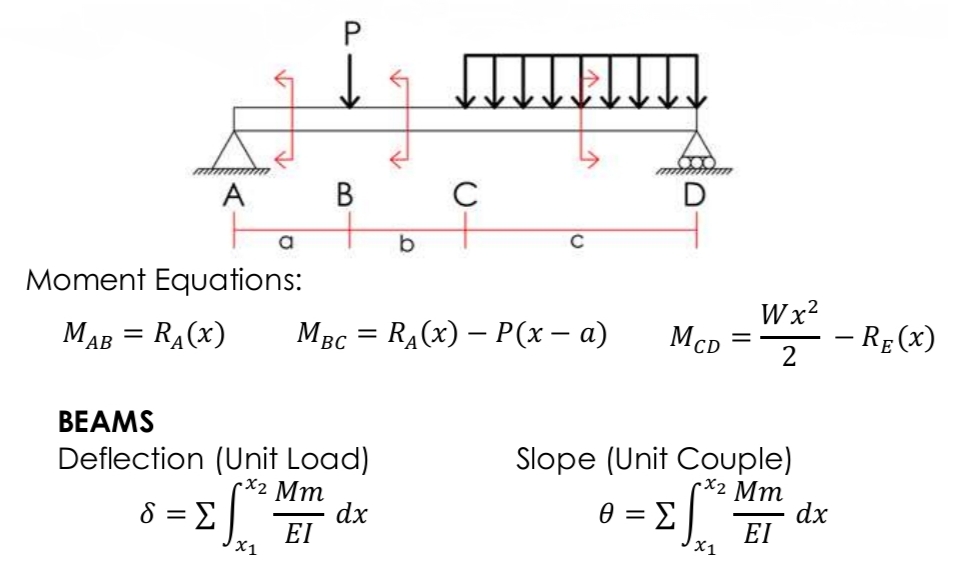
Trusses (Virtual Work Method)

Boundary Conditions

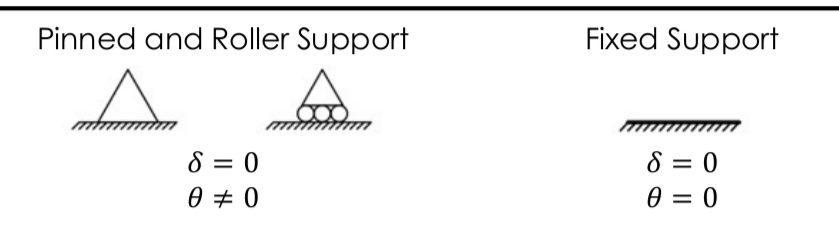
Fixed End Moment: Point Load

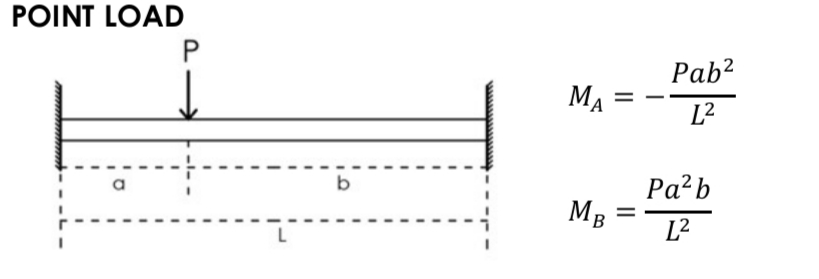
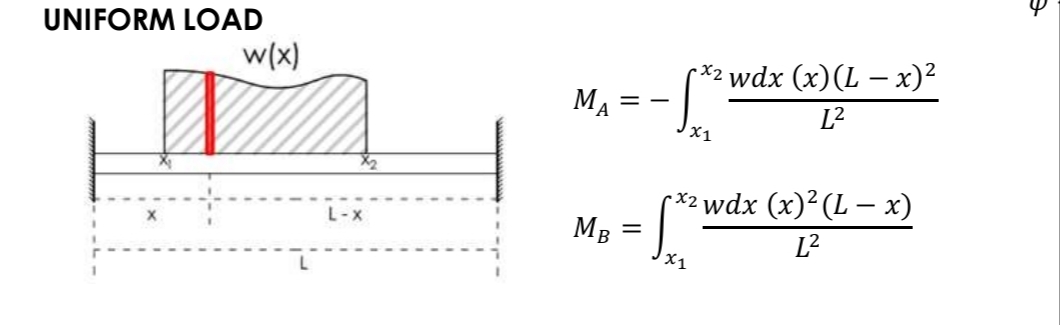
Fixed End Moment

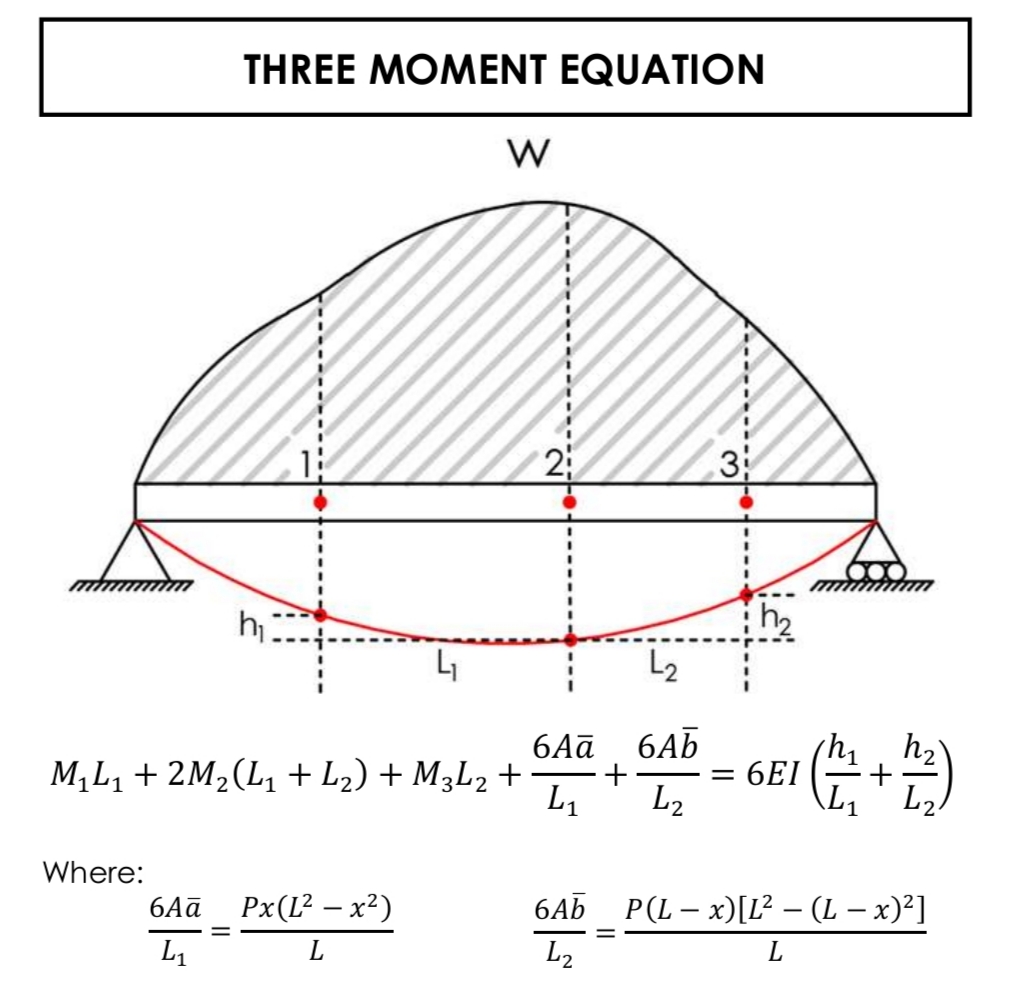
3 Moment Equation

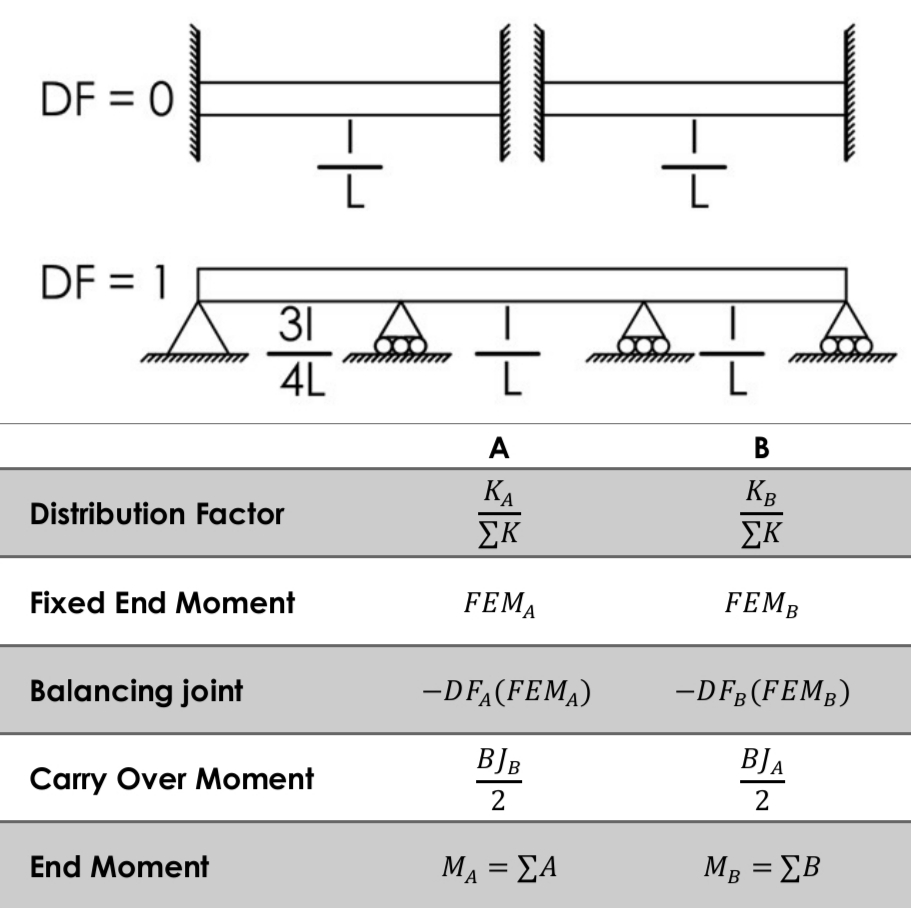
Moment Distribution Method

Slope Deflection Method

Stress: Simple Shear and Torsion

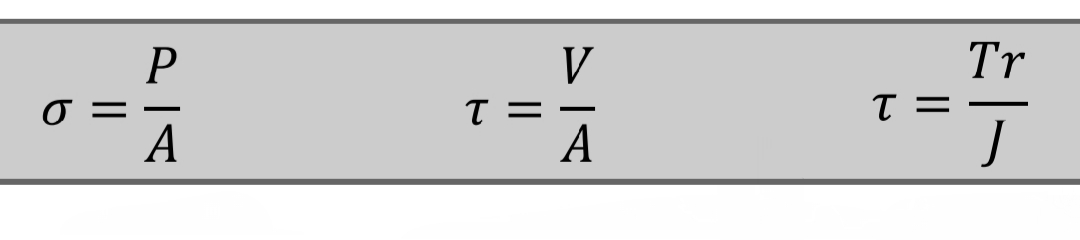
Strain: Simple Shear and Torsion

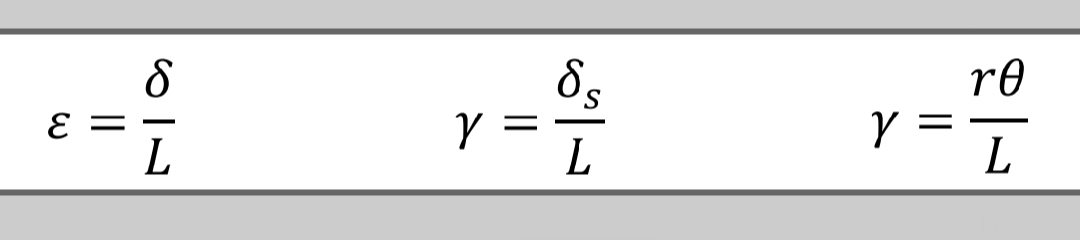
Modulus : Simple Shear and Torsion

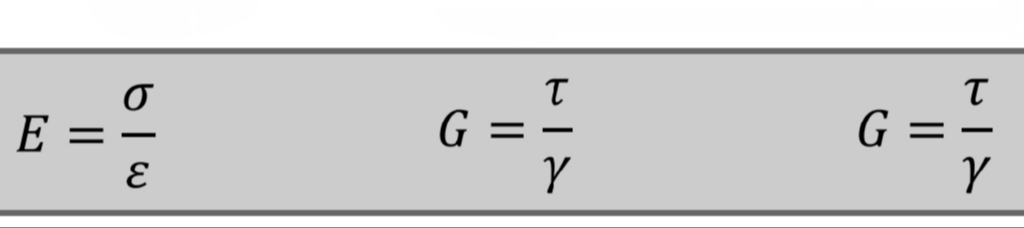
Deformation: Simple Shear and Torsion

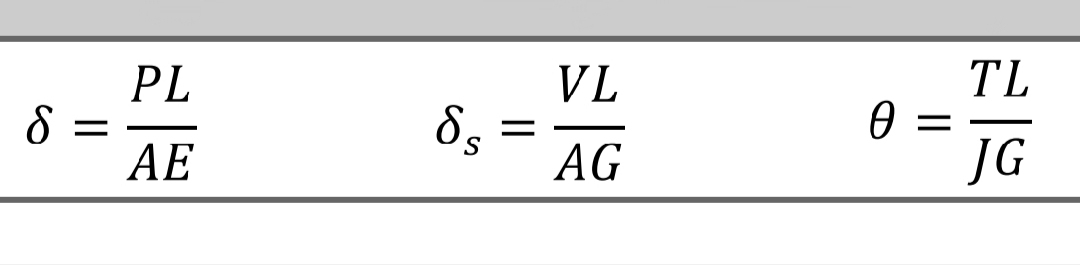
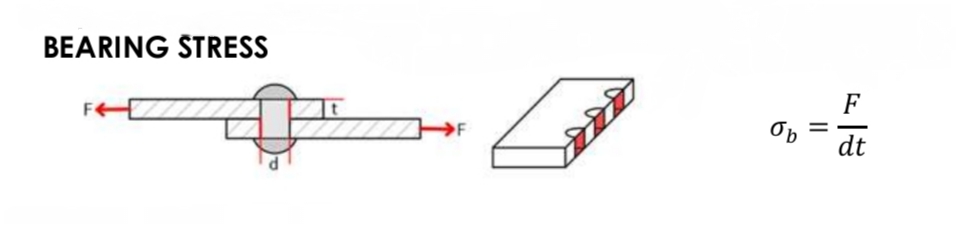
Bearing Stress of Bolt Connection

note: pick the more critical thickness

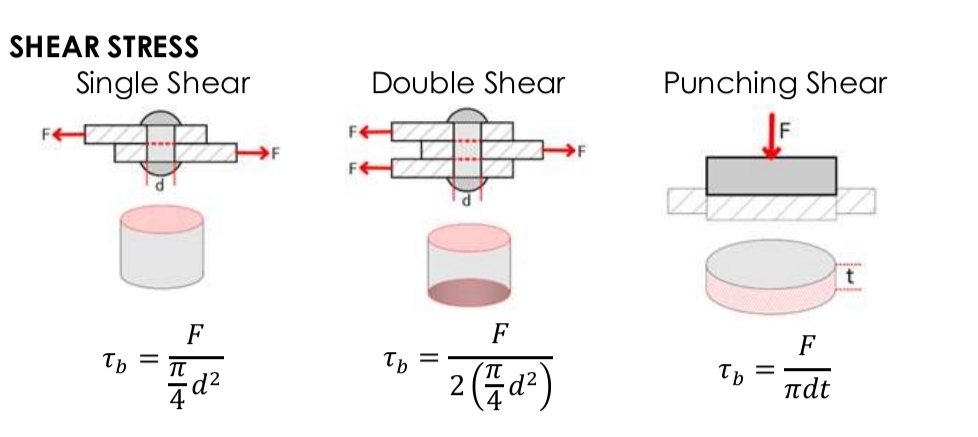
Shear Stress of Bolt Connection (3)

A material property that quantifies the ratio of transverse strain to axial strain when a material is subjected to axial stressx indicating the resistance to lateral deformation

Poisson’s Ratio

Poisson’s Ratio

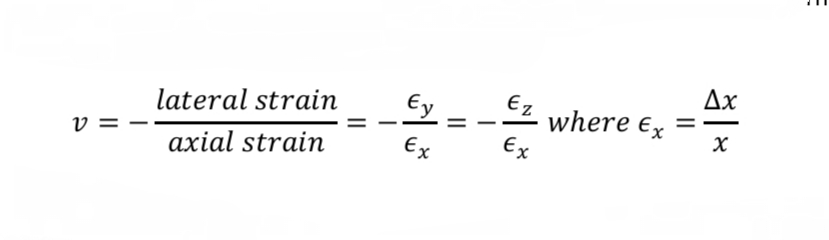
Deformation occurs in three dimensions due to the application of stress in three perpendicular directions

Triaxial Strain

Triaxial Strain

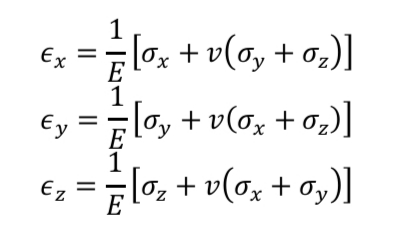
The change in volume of a material per unit volume, typically expressed as a ratio, resulting from aoplied stress or deformation

Volumetric Strain

Volumetric Strain Formula

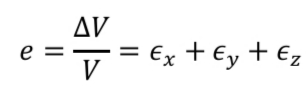
Modulus of Rigidity

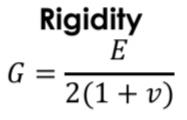
Resilience

Volumetric Strain when subjected to a hydrostatic pressure

The potential energy stored due to deformation cause by applied forces or stresses. It represents the work done to deform the material and is a measure of the materials’s ability to absorb and release energy during deformation

Strain Energy

Strain Energy Formula (3)

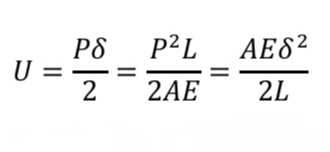
Thermal Stress Formula (3)

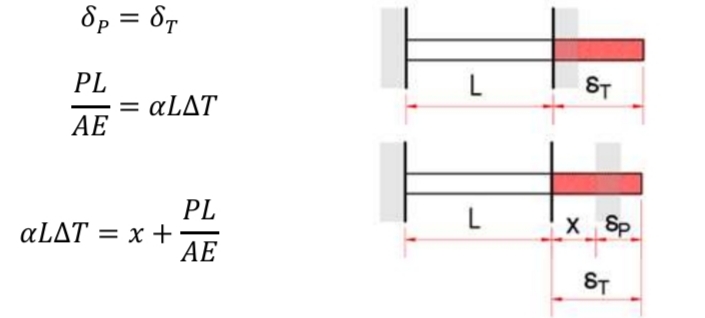
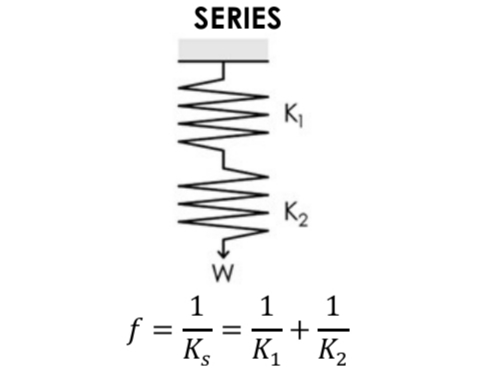
Helical Springs in Series

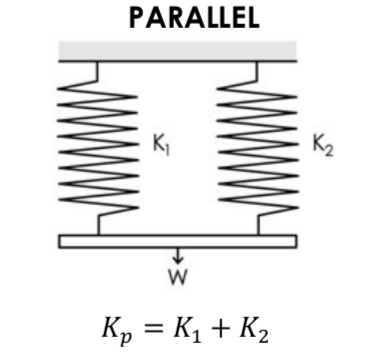
Helical Springs in parallel

Shear Strss in Helicscl Springs

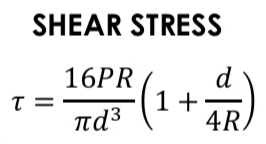
Elongation in Helical Springs

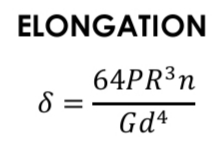
Spring Period in Helical Springs

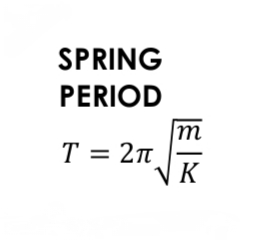
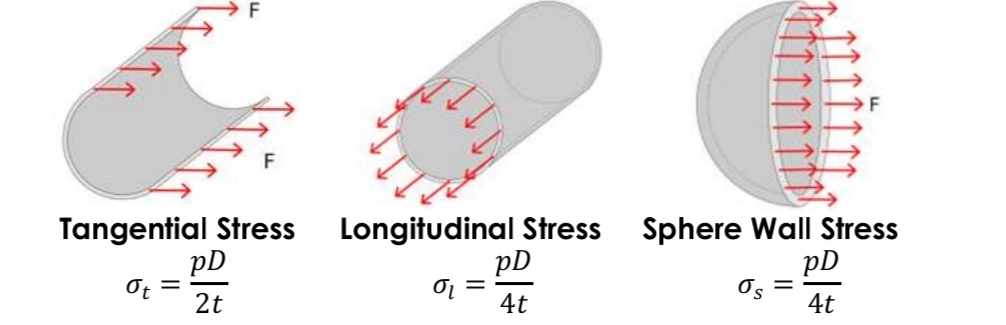
Stress in Pressure Vessels (3)

Flexural Stress in beams

Deformation in Flexure

Horizontal Shrar Stress

Maximum Shear Stress in Circular Beams (Solid and Hollow)

Max Shear Stress for Rectangular and Triangular Beams

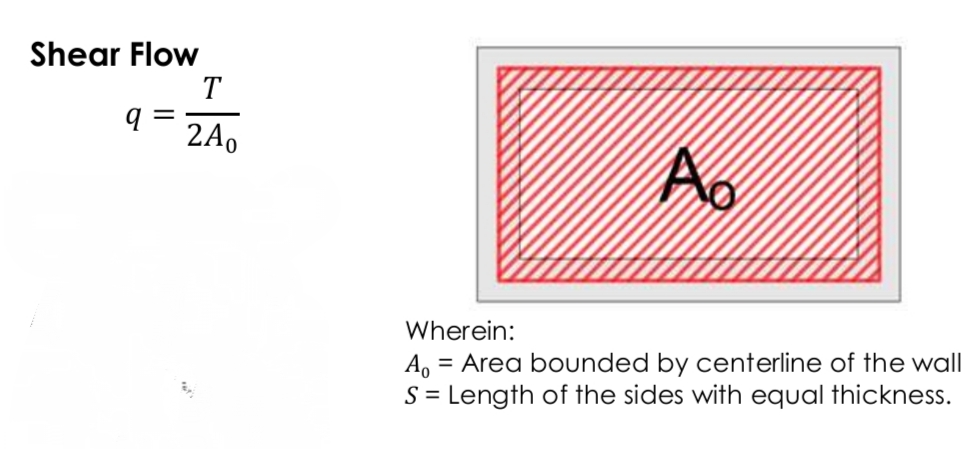
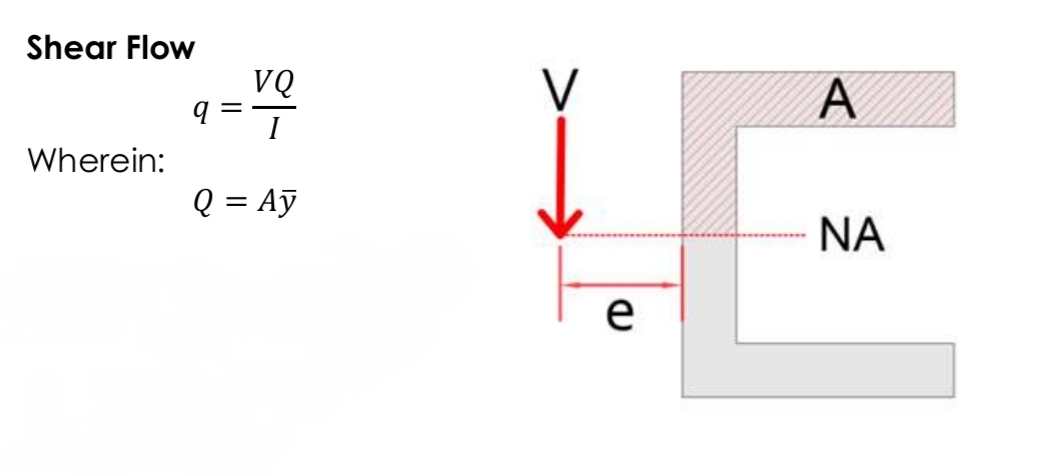
Shear Flow of thin-walled tube

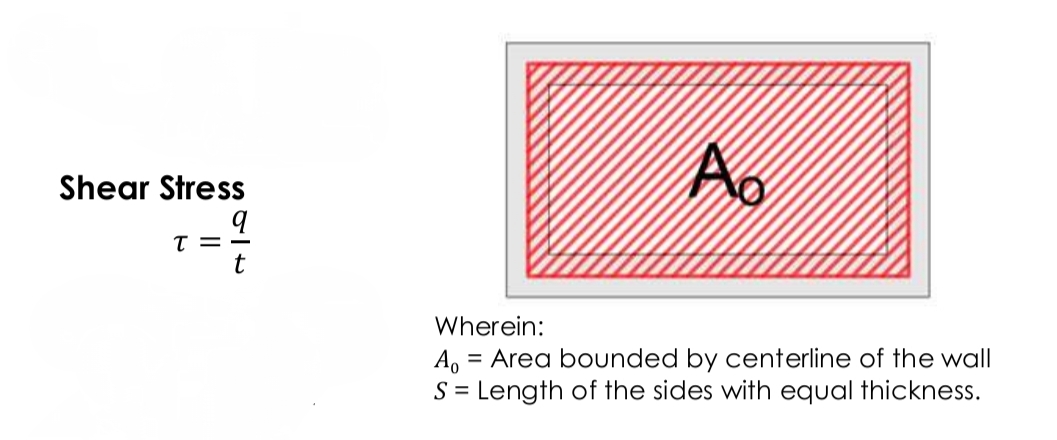
Shear Stress of thin walled tube

Angle of twist of thin walled tube

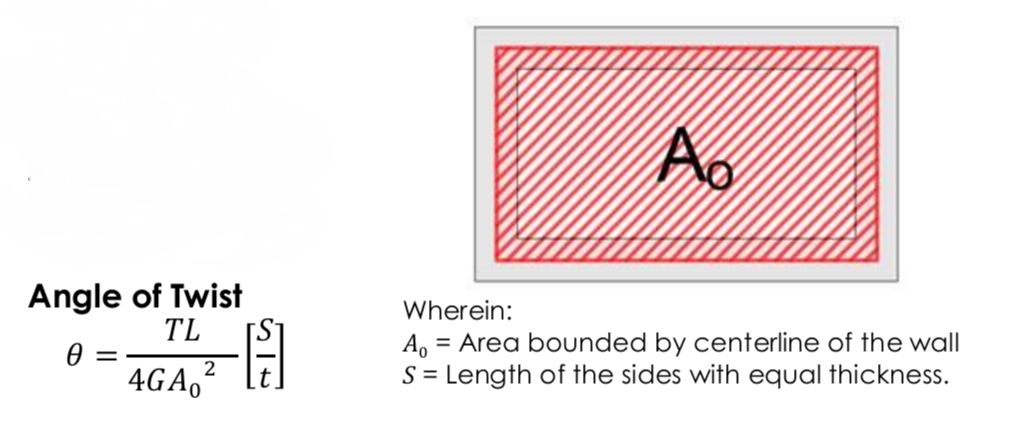
Shear flow of thin walled member

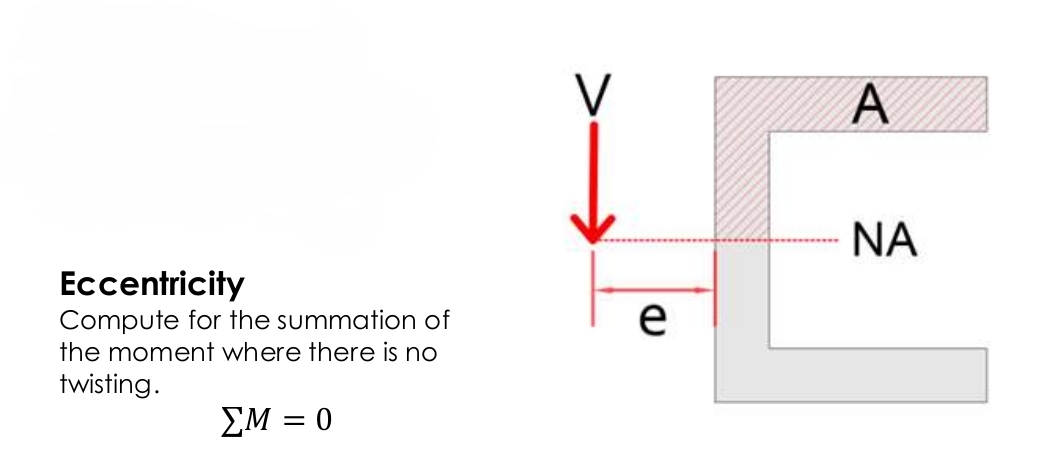
Eccentricity of thin walled member

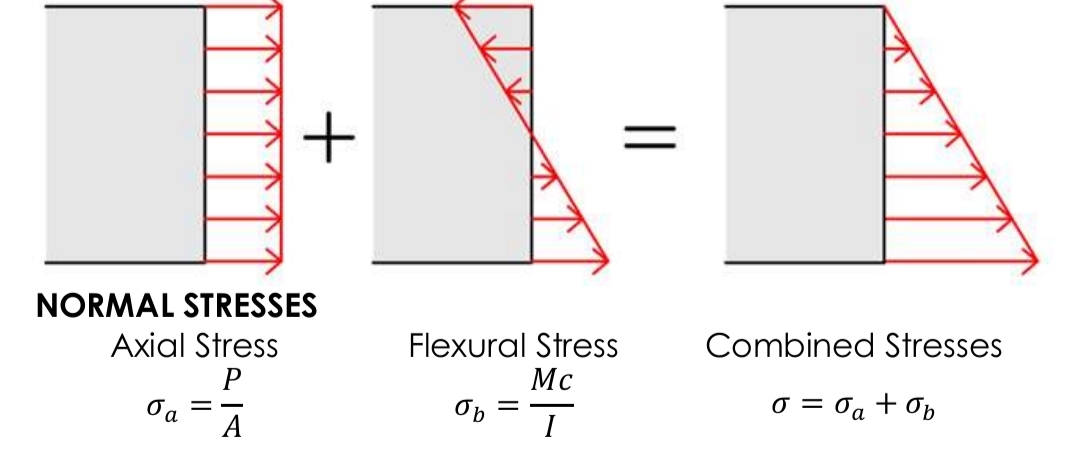
Combined Normal Stresses

Combined Shear Stress

Mohr’s Circle Sign Conventions

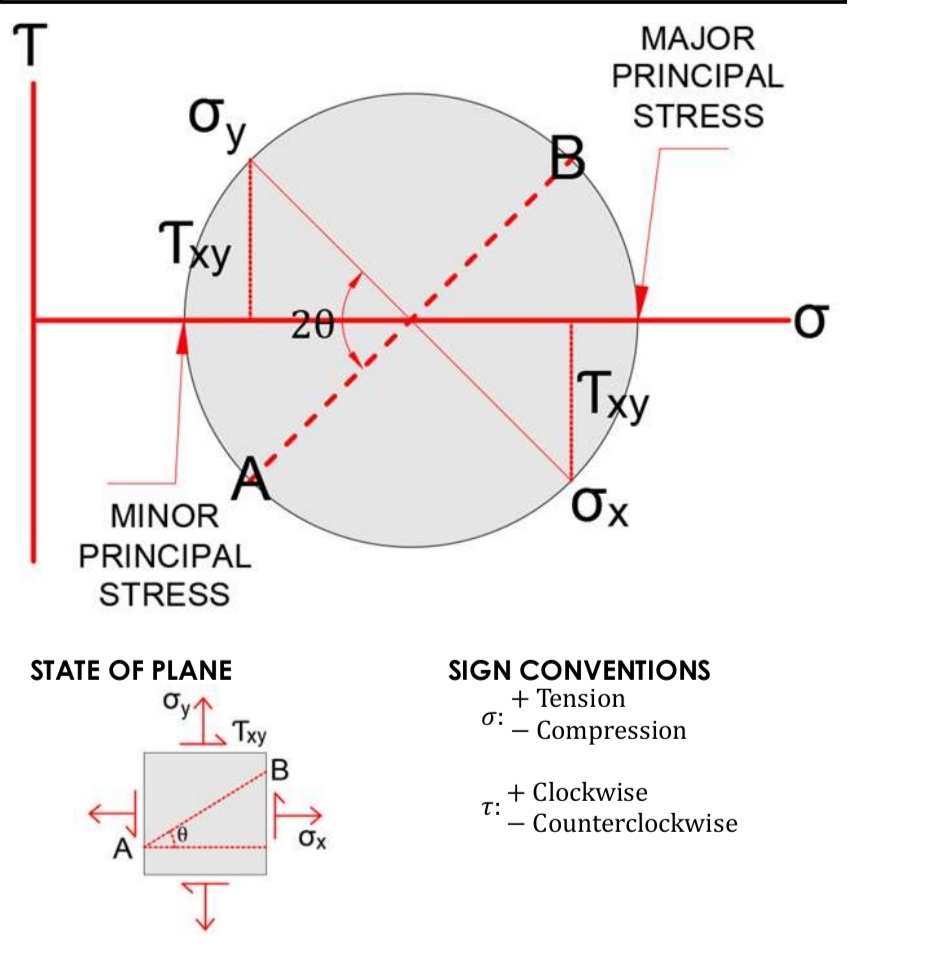
Mohr’s Circle Cal Tech

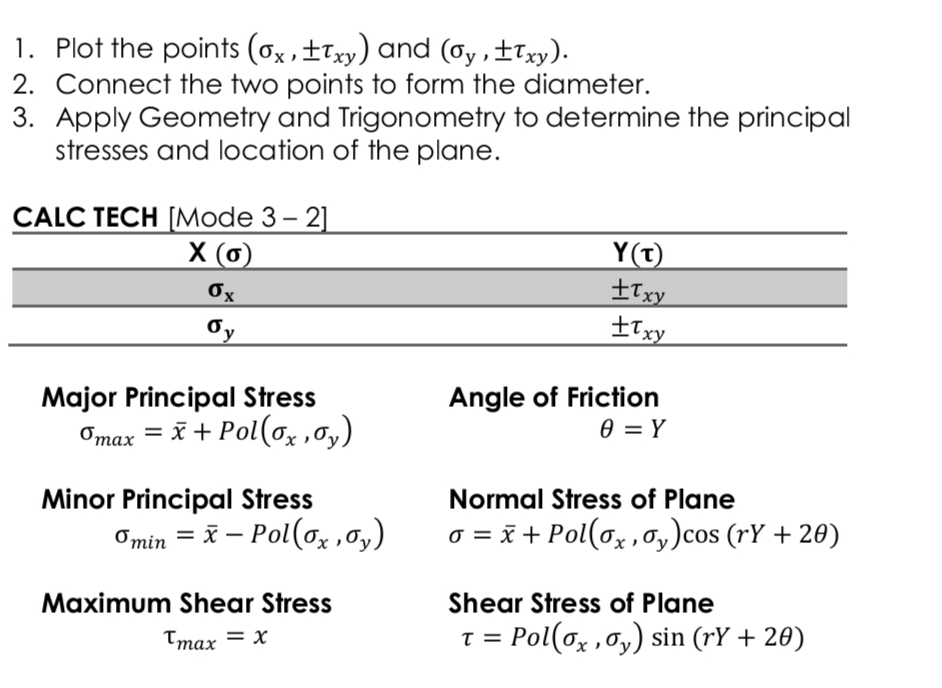
Thermal Stress

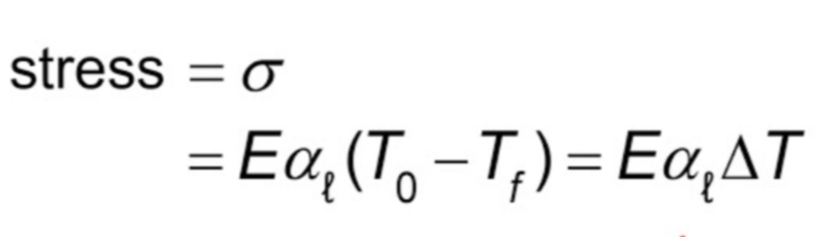
Cal Tech when of the resultant of forces with different angles

Complex Mode F<Angle

Add all angles : A+Bi. A will be the Rx and B will be the Ry

Abs(Ans) : Resultant

Radius of Curvature

R = EI/M

R= Ec/F

Deflection using Radius of Curvature

y= R-Rcos(theta/2)