Waves

Wave terms

Wavelength, λ: length of one complete wave

Time period, T: time taken for one wave to pass

Frequency, f: the number of waves that pass every second

wave equation

v = fλ

• v = wave speed (ms^-1)

• f = frequency (Hz)

• λ = wavelength (m)

Refraction

Change in speed and direction when waves enter a new medium

• When speed increases, light bends away from normal

• When speed decreases, light bends towards normal

Refractive index

refractive index (n) = c in vacuum / c in medium

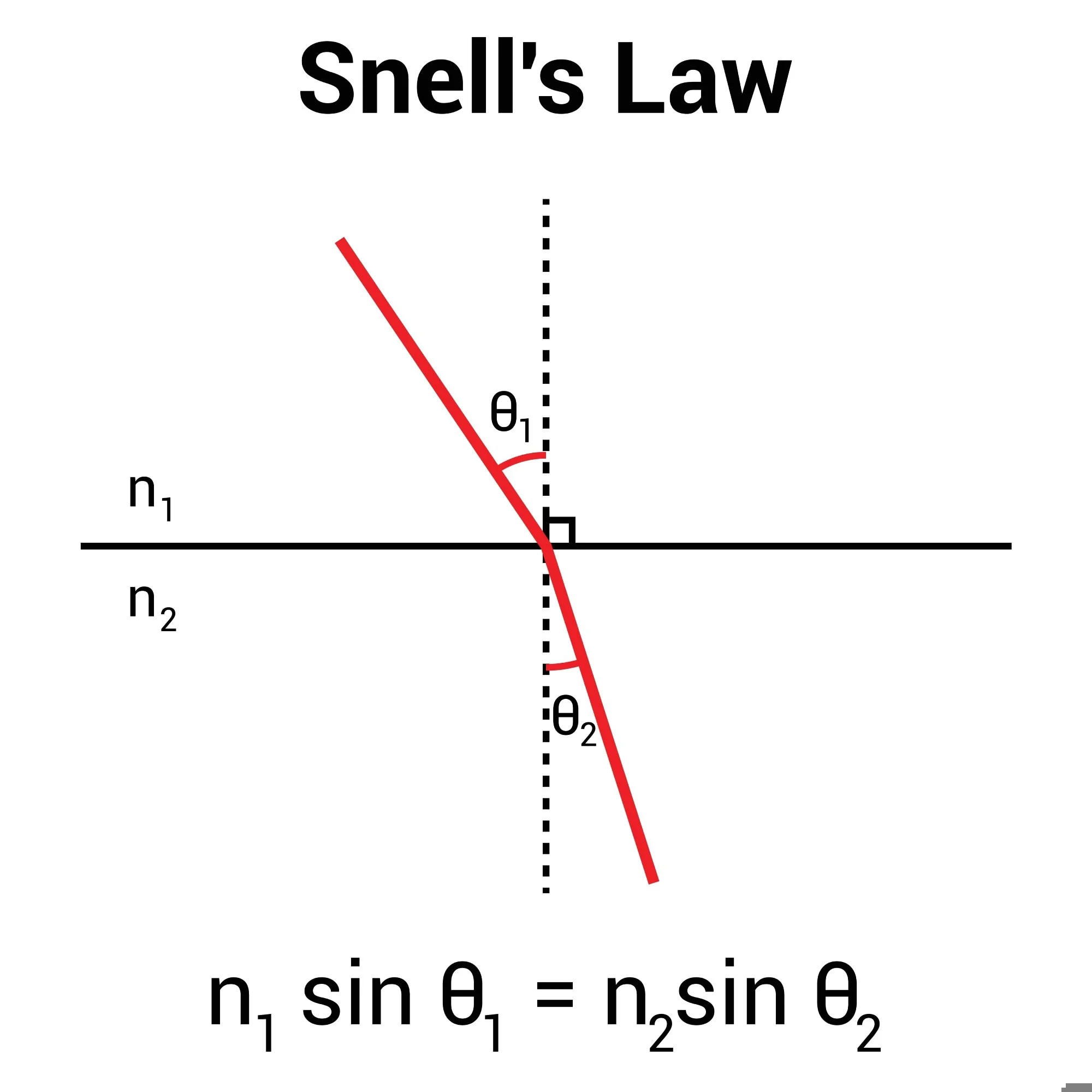
Snell’s Law

n₁sinθ₁ = n₂sinθ₂

features of a wave during diffraction

• Wavelength and and speed change

• Frequency stays the same

Total Internal Reflection

Occurs when all light is reflected at a boundary between two different media

Conditions for Total Internal Reflection

incident angle > critical angle

• all light reflects

incident angle = critical angle

• total internal reflection

incident angle < critical angle

• light reflects out

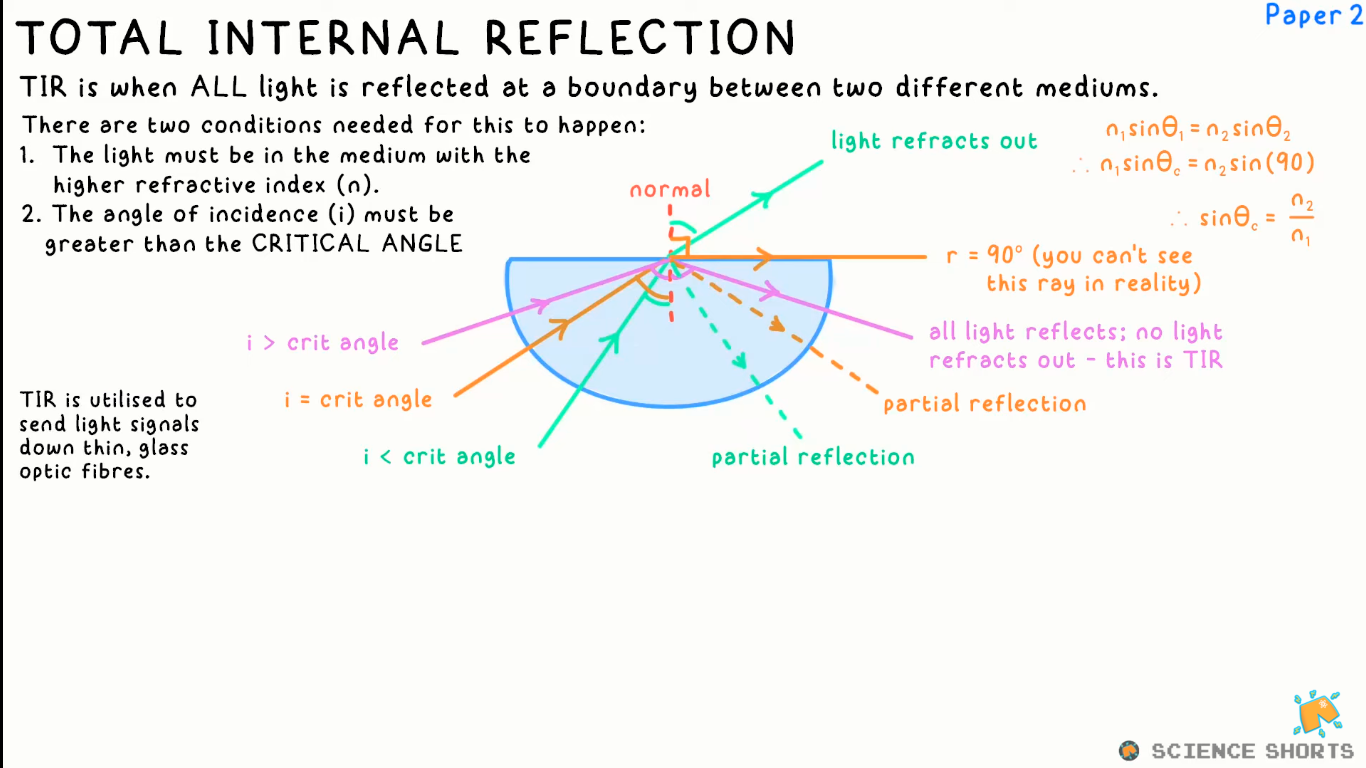
Critical angle

Incident angle at which total internal reflection occurs

• n₁sinθ_{c =} n₂sinθ(90)

• In air, n₂ = 1:

  • n₁sinθ_c = 1 x 1

  • sinθ_{c =} 1/n₁

Polarisation

Transverse waves can be made to oscillate along the same plane

Only transverse waves can be polarised: EM waves are transverse

Progressive wave

Transforms energy from one place to another, without transporting matter

Phase difference

Δd / λ

• Separation / wavelength

(Δt / T) x 2π or 360 degrees

Stationary Waves

The result of the interference between 2 waves travelling in opposite directions

• They must have the same frequency and wavelength

Phase difference in stationary waves

In phase: both above / below equilibrium

In antiphase: one above one below equilibrium

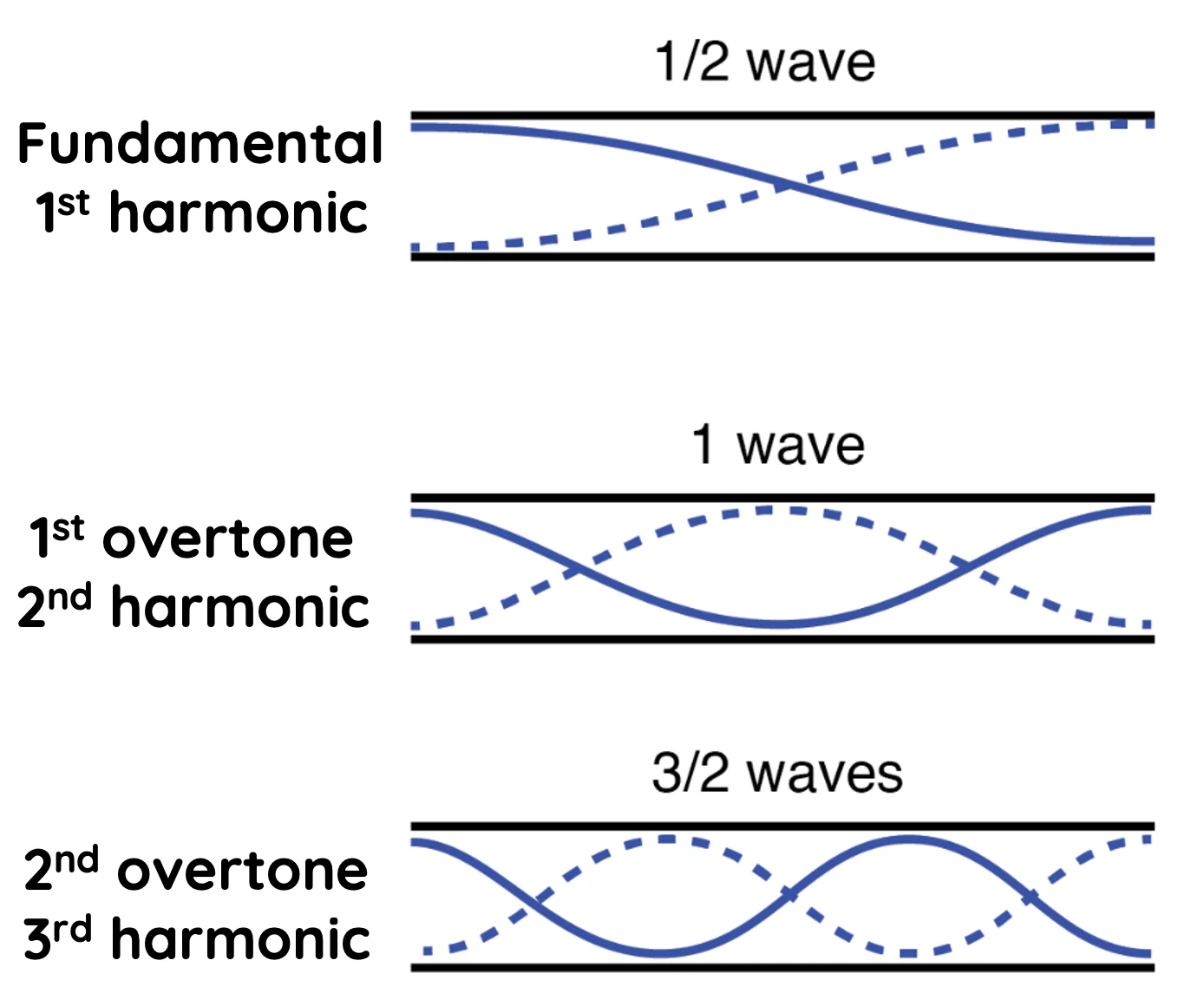
Stationary waves

• Fundamental → L = ½ λ

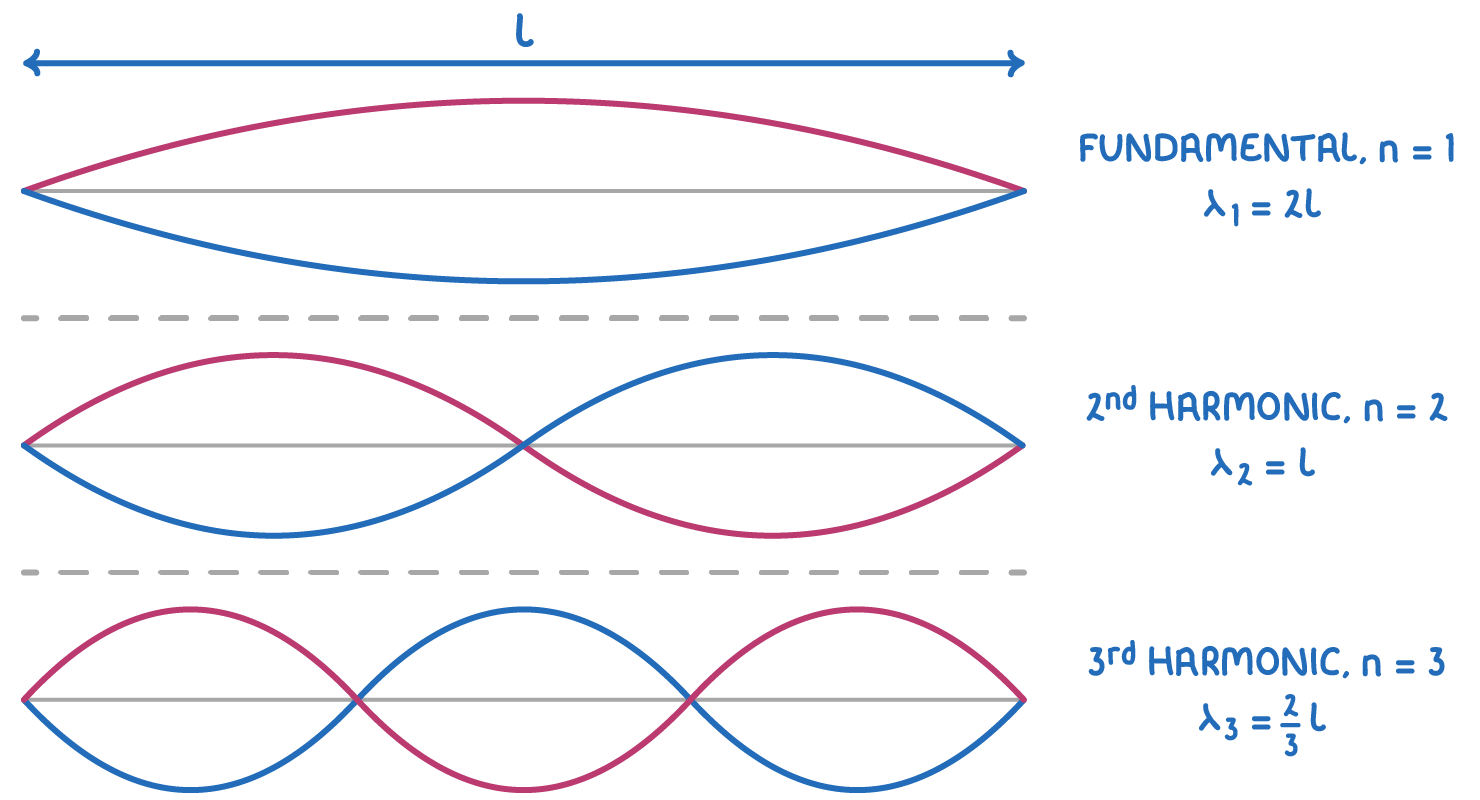
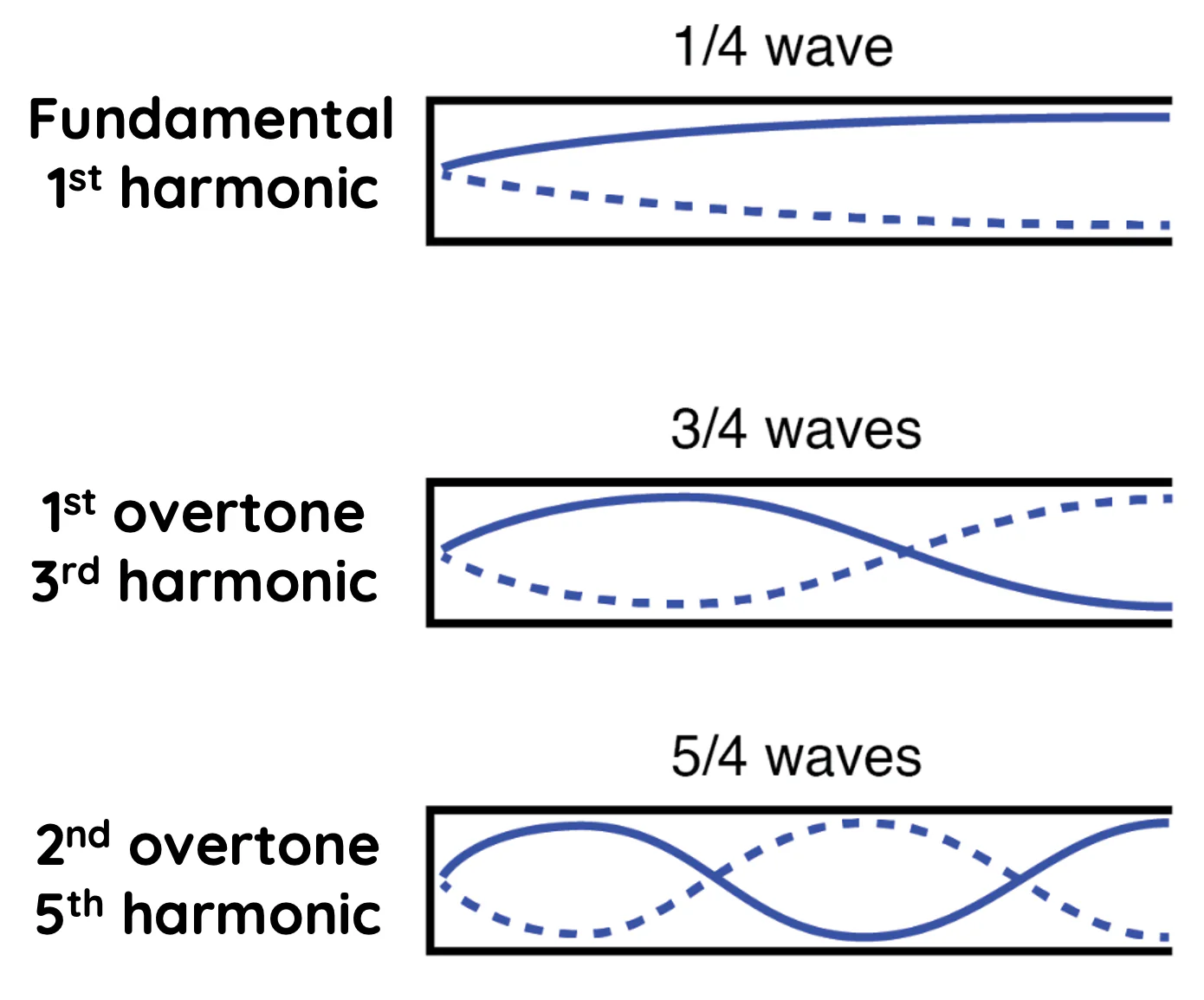
Stationary waves in a closed tube

Fundamental → L = ¼ λ

Stationary waves in an open tube

Fundamental = ½ λ

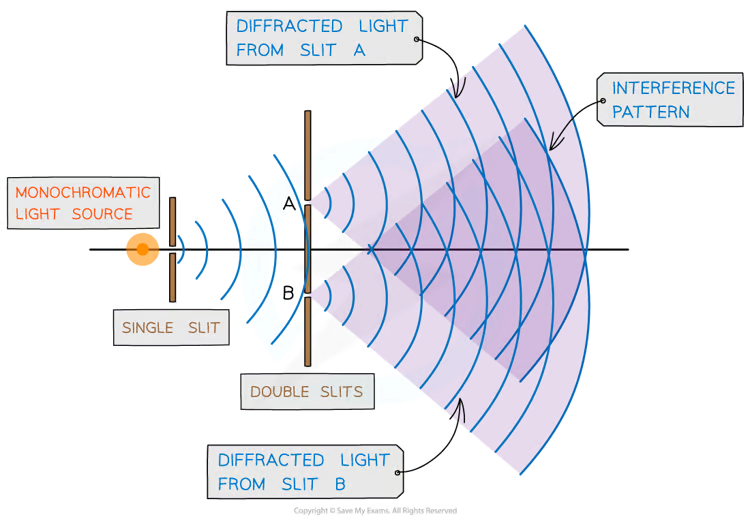
Double Slit Experiment

Minimum: path difference of multiples of 1/2 λ

Maximum: path difference of 0

Demonstrates the wave-like nature of light with the bright and dark fringes being characteristic pattern to waves (constructive/destructive interference)

Coherent waves

Constant phase relationship.

A coherent light source is required for the double slit experiment for the interference pattern to be present

Path Difference

The difference in distance that two waves must travel from their sources to a given point

Wavelength from double slit experiment

λ = ax / D

• a = fring spacing

• x = slit separation

• D = distance to screen

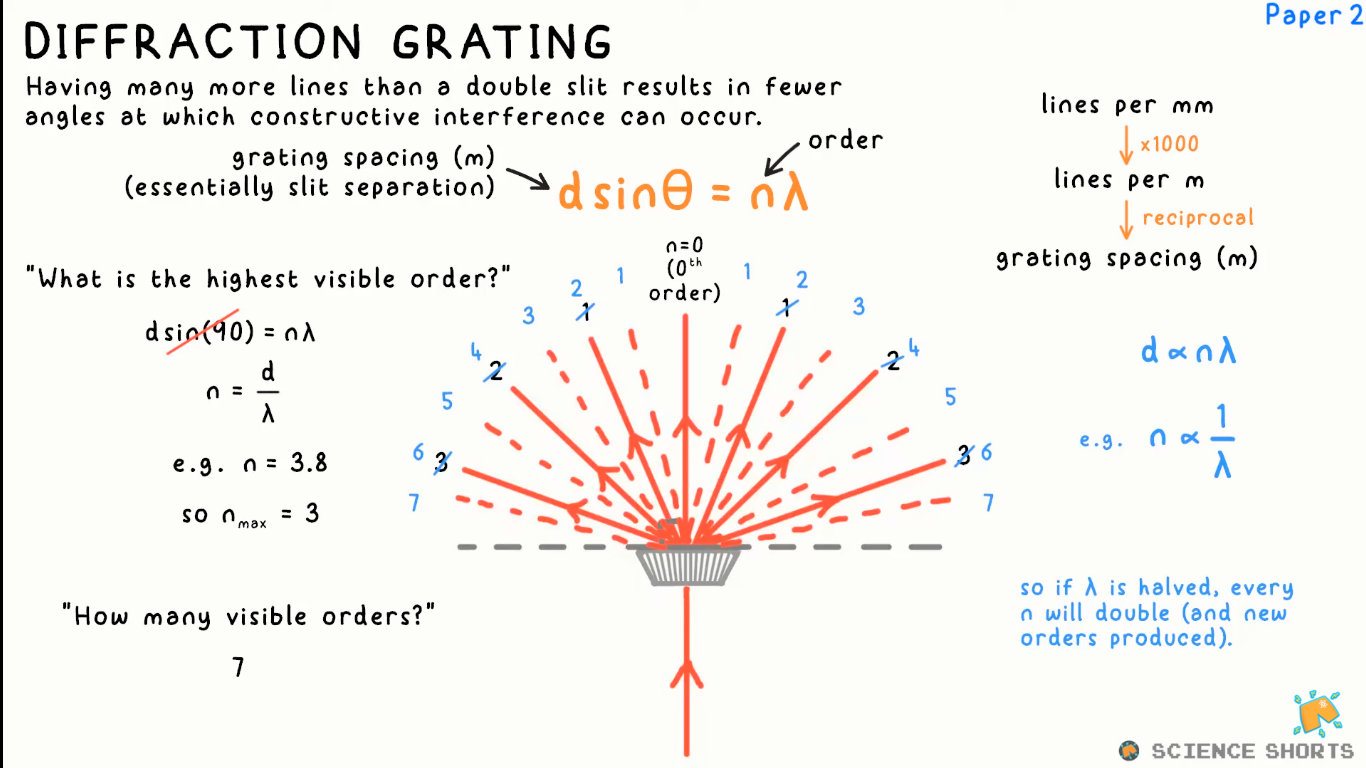
Diffraction grating

A grating with many slits means there are fewer angles far from central maximum at which constructive interference occurs → orders

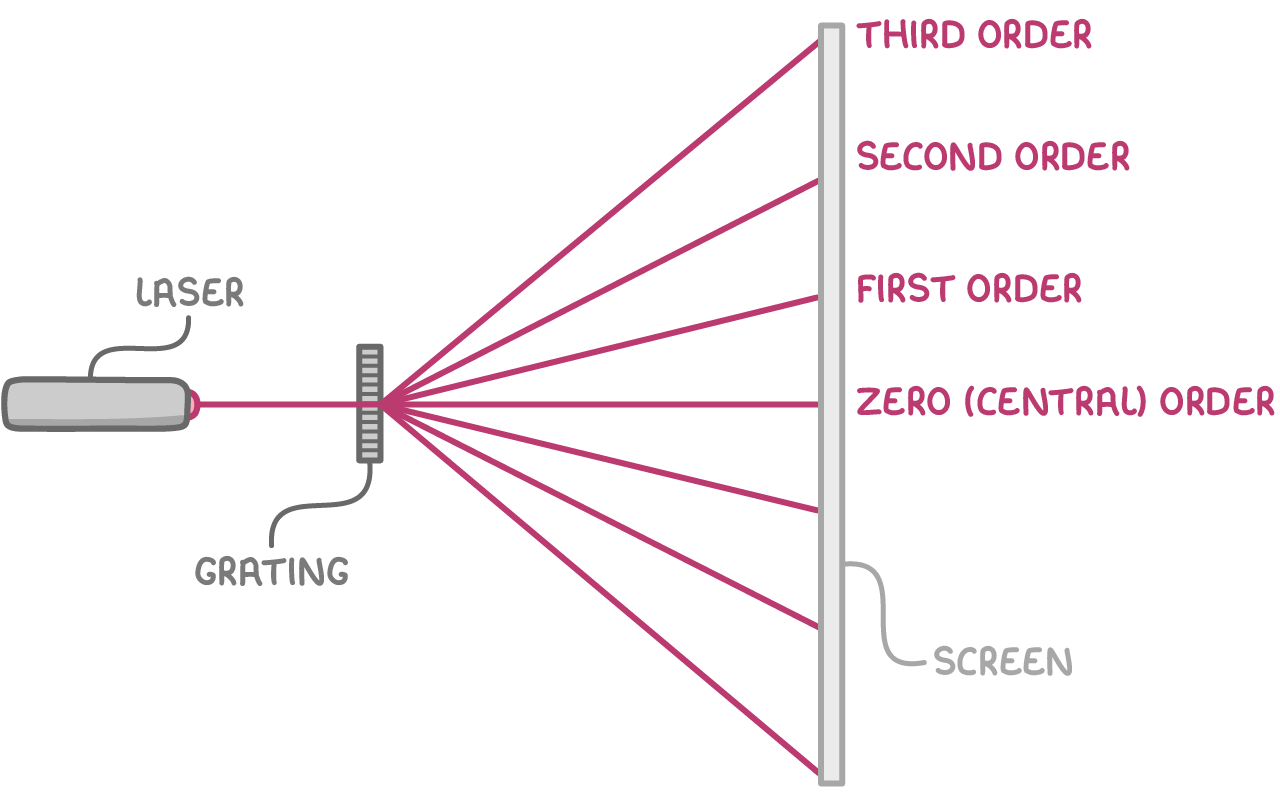
Diffraction grating equation

NOT IN FORMULA SHEET

d sin θ = n λ

• d = grating spacing (m)

• n = order (i.e: 1st order, 2nd order…)

• θ = angle with zero order maximum

grating spacing

lines per mm (mm^-1)

• x 1000

lines per m (m^-1)

• reciprocal

grating spacing (m)

Highest visible order

d sin(90) = n λ

• n_max = d / λ (rounded down)

visible orders = 2 x n_max + 1

• 2 of the orders on each side + zero order maximum