CS 312 Midterm

Fibonacci Sequence Algorithm

if n<2 then

   return n

return Fib(n-1) + Fib(n-2) 

Fibonacci Redux

Fib2(n)
   fib[0] = 0
   fib[1] = 1
   for i = 2 to n do
      fib[i] = fib[i-1] + fib[i-2]
   return fib[n]

f(n) in O(g(n))

lim f(n)/g(n) = 0

f(n) in THEATA(g(n))

lim f(n)/g(n) = Real Number

f(n) in OMEGA(g(n))

lim f(n)/g(n) = Infinity

Handy Rules for Big-O

1. Constants don’t matter

2. Polynomial order matters

3. Exponential dominates polynomial

4. Exponential base matters

5. Polynomial dominates logarithm

6. Logarithm base doesn’t matter

Addition Time Complexity

O(n)

Basic Multiplication Time Complexity

O(n²)

Modular Addition Time Complexity

O(n)

Modular Multiplication Time Complexity

O(n²)

Modular Division Time Complexity

O(n³)

Modular Exponentiation Algorithm

if y = 0 then
   return 1
z = modexp(x, y//2, N)
if y is even then
   return z**2(mod N)
else
   return x * z**2 (mod N)

Modular Exponentiation Time Complexity

O(n³)

Primality Test (Fermat)

PrimeTest(N)
   choose int(a) in range(N)
   if a**(N-1) (mod N) == 1 then
      return 'Yes'
   else
      return 'No'

PrimeTest2(N)
   for i = 1 to k do
      if PrimeTest(N) = 'No' then
         return 'No'
   return 'Yes'

Generating Primes Time Complexity

O(n⁴)

RSA Process

1. Pick two primes p, q and let N = pq

2. Choose e relatively prime to (p -1)(q -1)

3. Find d such that de mod((p -1)(q -1)) = 1

4. Encrypt message x as x^e mod N = y

5. Decrypt code y as y^d mod N = (x^e)^d mod N = x^de mod N = x

Euclid’s Algorithm

if b = 0 then
   return a
return Euclid(b, a%b)

Extended Euclid’s Algorithm

if b = 0 then
   return (1,0,a)
x, y, z = extEuclid(b, a%b)
return (y, x - ((a//b)*y), z)

Modular Division Lemma

For any positive integers a and b, the Extended Euclid algorithm returns integers x, y, and z such that GCD(a,b) = z = ax + by

Total RSA Time Complexity

O(n⁴)

Miller-Rabin Algorithm

def miller_rabin(N: int, k: int) -> str:
    for i in range(k):
        a = random.randint(1, N-1)
        y = N - 1
        x = mod_exp(a, y, N)
        if x != 1:
            return 'composite'
        while x == 1 and y%2 == 0:
            y = y//2
            x = mod_exp(a, y, N)
        if x != N-1 and x != 1:
            return 'composite'
    return 'prime'

Probability of getting the correct answer from Fermat

1− 1/(2^𝑘)

Probability of getting the correct answer from Miller-Rabin

1− 1/(4^𝑘)

Divide and Conquer Time Complexity

T(n) = a* T(n/b) + O(divide & combine time)

Master Theorem

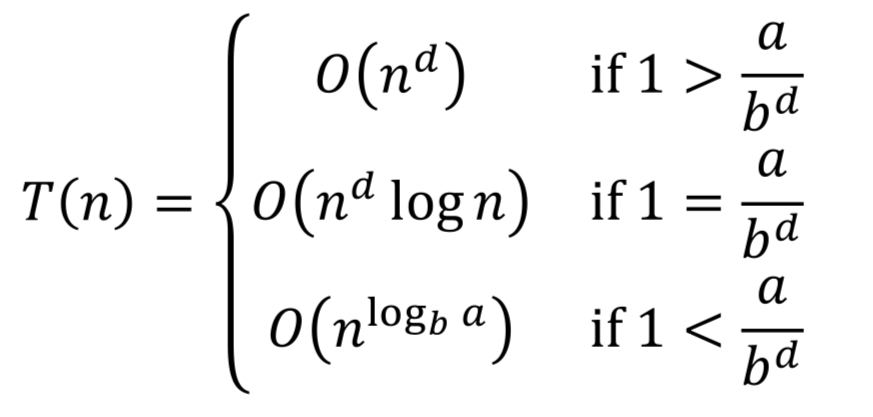
Merge & Merge Sort Algorithms

MergeSort(x)
   if len(x) <= 1 then
      return x
   left = MergeSort(x[:len(x)//2])
   right = MergeSort(x[len(x)//2:])
   y = Merge(left, right)
   return y

Merge(l, r)
   result = []
   while len(l) or len(r) do
      if l[0] <= r[0] then
         result.append(l[0])
         l.delete(0)
      else
         result.append(r[0])
         r.delete(0)
   return result

D&C Multiplication Time Complexity

O(n²)

D&C Faster Multiplication Time Complexity

O(n^1.59)

MergeSort Time Complexity

O(n log(n))

General Median Time Complexity

O(n log(n))

Faster D&C Median Time Complexity

O(n)

Matrix Multiplication Time Complexity

O(n³)

Convex Hull Find Upper Tangent Algorithm

p = rightmost point in L 
q = leftmost point in R
temp = line(p,q)
done = False
while not done do
   done = True
   while temp is not upper tangent to L do
      r = counterclockwise neighbor of p
      temp = line(r, q)
      p = r
      done = False
   while temp is not upper tangent to R do
      r = clockwise neighbor to q
      temp = line(p,r)
      q = r
      done = False
return temp

Convex Hull Algorithm

if len(points) < 3 then
   return points
mid = len(points)//2
L = convexHull(points[:mid])
R = convexHull(points[mid:])
upL, upR = findUpper(L,R)
lowL, lowR = findLower(L,R)
combined = L[:upL]+R[upR:lowR]+L[lowL:]
return combined

Depth-First Search of Undirected Graph

DFS(G)
   for all v in V do
      visited(v) = False
   for all v in V do
      if not visited(v) then
         Explore(v)

Explore(G, v)
   visited(v) = True
   previsit(v)
   for each edge (u,v) in E do
      if not visited(v) then
         Explore(v)
   postvisit(v)

Depth First Search Data Structure

Stack

Tree Edge

u_pre <= v_pre <= v_post <= u_post

Forward Edge

u_pre <= v_pre <= v_post <= u_post

Back Edge

v_pre <= u_pre <= u_post <= v_post

Cross Edge

v_pre <= v_post <= u_pre <= u_post

A directed graph has a cycle if and only if ___________

the DFS tree has a backward edge

How to Linearize a DAG

1. Do DFS then linearize by decreasing post order

2. Iteratively add source vertices to the linearization and remove them from the graph

Strongly Connected Component definition

A set of vertices that are all connected to each other

Finding Strongly Connected Components Algorithm

G_r = ReverseEdges(G)
post = DFS(G_r)
scc = DFS(G,post)
return scc

Strongly Connected Components Time Complexity

O(|V| + |E|)

Depth First Search Time Complexity

O(|V| + |E|)

Breadth-First Search Algorithm

for all u in V do
   dist(u) = infinity
dist(s) = 0
Q.inject(s)
while Q in not empty do
   u = Q.eject()
   for all edges (u,v) in E do
      if dist(v) = infinity then
         Q.inject(v)
         dist(v) = dist(u) + 1
return dist

BFS Time Complexity

O(|V| + |E|)

Dijkstra’s Algorithm

for all u in V do
   dist(u) = infinity
   prev(u) = null
dist(s) = 0
H.makequeue(V, dist)
while H is not empty do
   u = H.deletemin()
   for all edged(u,v) in E do
      if dist(v) > dist(u) + l(u,v) then
         dist(v) = dist(u) + l(u,v)
         prev(v) = u
         H.decreasekey(v)
return dist,prev

Dijkstra Time Complexity

O(MakeQueue + DeleteMin * |V| + DecreaseKey * |E|)

Dijkstra Space Complexity

O(|V| + |E|)

Array Priority Queue Function Times

• insert: O(1)

• decrease-key: O(1)

• delete-min: O(n)

• make-queue: O(n)

Binary Heap Priority Queue Function Times

• insert: O(log(n))

• decrease-key: O(log(n))

• delete-min: O(log(n))

• make-queue: O(n log(n))

Breadth First Search Data Structure

Priority Queue

Bellman-Ford Algorithm

for all u in V do
   dist(u) = infinity
   prev(u) = null
dist(s) = 0
for i = 1 to |V|-1 do
   for all edges (u,v) in E do
      if dist(v) > dist(u) + l(u,v) then
         dist(v) = dist(u) + l(u,v)
         prev(v) = u
return dist,prev

Bellman-Ford Time Complexity

O(|E| * |V|)

Greedy Philosophy

• Build up solution piece by piece

• Always choose the next piece that offers the most obvious and immediate benefit without violating given constraints

Prim’s Algorithm

for all u in V do
   cost(u) = infinity
   prev(u) = null
choose random node u_0
cost(u_0) = 0
H.makequeue(V) {costs as keys}
while H is not empty do
   v = H.deletemin()
   for each (v,z) in E do
      if cost(z) > l(v,z) then
         cost(z) = l(v,z)
         prev(z) = v
         H.decreasekey(z)
return cost,prev

Prim’s Algorithm Time Complexity

O(MakeQueue + DeleteMin * |V| + DecreaseKey * |E|)

Kruskal’s Algorithm

for all u in V do
   makeset(u)
X = {}
sort edges e by weight
for all edges {u,v} in E in increasing order of weight do
   if find(u) != find(v) then
      X = X U {u,v}
      union(u,v)
return X

Kruskal’s Algorithm Time Complexity

O(|E| log(|V|))

Array implementation of PQ is better in _______ graphs.

Dense

Binary heap implementation of PQ is better in _______ graphs.

Sparse

Huffman Algorithm

T = null
H.makequeue(S) #S is a set of symbols, frequency f as keys
for k = |S| to 2|S| - 2 do
   i = H.deletemin()
   j = H.deletemin()
   f(k) = f(i) + f(j)
   H.insert(k)
   k.left = i
   k.right = j
   T.addnode(k)
return T

Huffman Algorithm Time Complexity

O(n log(n))

E[bits/character] =

Σ f(s) c(s)

Entropy =

-Σ f_i log₂(f_i)

Huffman works best when entropy is _____________

Low

Horn Formula

T = {}
for x in Formula do
   T.insert(x:False)
while there is an unsatisfied implication in F using T do
   T[z] = True
if all negative clauses are satisfied by T then
   return T
else
   return None

2-SAT Algorithm (in words)

Set up nodes in graph for positive and negative variables. Add edges based on implications. Look for cyclical pattern(s) in the graph.

Set Cover Theorem

Given set cover problem P = (U, S), if the optimal set cover is C*, then the greedy algorithm finds a cover C such that |C| <= |C*| ln|U|

Set Cover Corollary

No approximation algorithm got the set cover problem can do better than the greedy algorithm, unless P = NP.