CHI-SQUARED TESTS - CH6

what is the null hypothesis in a goodness of fit test

H0: there is no difference between the observed and the theoretical distribution

what is the alternate hypothesis in a goodness of fit test

H1: there is a difference between the observed and the theoretical distribution

measure of goodness of fit formula:

where Oi = observed value

Ei = expected value

 

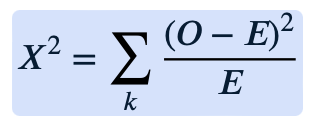
what does a lager goodness of fit mean?

the less similar the distributions are

number of degrees of freedom =

number of columns - number of constraints (e.g always take a way one, but also when estimating parameters)

what must you make sure of when looking at expected values

if an expected value is less than 5, you must combine it with another cell in the table until they’re greater than 5

to find critical values…

use the test statistic and the degrees of freedom and then go to the tables

if the X² from the tables is less than you’re calculated value…

reject H0

if discrete random variable X is defined over k values, p=

1/k

for testing the goodness of fit of a binomial distribution, what’s the first step?

find the probability of each value of x by just subbing into calculator, i.e. P(X=0), P(X=1)…

then calculate expected frequencies for each

hypotheses for a goodness of fit test for a distribution

H0: binomial, poisson etc is suitable model

H1: it isn’t

how to calulate p for a binomial test if it isn’t given

p = Σ r•f / Nn

where:

Σ r•f = the sum of multiplying the columns in the table up, i.e a score of 6 ( r ) occurred 4 times (f)

N = the number of observations, or total frequency

n = the number of trials, or maximum value of r

how to approximate λ for a Poisson goodness of fit calculation

Σ r•f / N

what are contingency tables

a scenario in which there are multiple events, i.e. what grade a student got and whether they’re a boy or a girl

hypotheses for a contingency table test

H0: event 1 and event 2 are independent

H1: event 1 and event 2 are not independent

expected frequency for a contingency table

row total • column total / grand total

degrees of freedom for a contingency table

(number of columns -1)(number of rows -1)

approximate p for a geometric distribution goodness of fit test

N / Σr•f

where N is the total number of successes

expected frequency for geometric

p•(1-p)^n multiplied by the total frequency