MCAT: General Chemistry Chapter 1 (KAPLAN)

isotopes

different number of neutrons in atoms, same atomic number but have different mass number -- they exhibit similar chemical properties and are normally labeled by their mass number (carbon 12) except in hydrogens (protium, deuterium, and tritium)

mass number

sum of protons and nucleus in nucleus -- changes with each varying isotope

valence electrons

farthest electrons from the nucleus and because they are so far, they feel the least amount of electrostatic pull from the nucleus and therefore can bond with others (interact with their surrounding environment) -- determine reactivity of an atom

most easily removed

"active" electrons

dominate the chemical behavior of an atom

Electron energy levels

electrons closer to the cell nucleus have lower energy levels, and farther away have higher energy levels

which subatomic particle is most important for determining: charge?

electron

which subatomic particle is most important for determining: atomic number?

proton

which subatomic particle is most important for determining: isotope?

neutron

how to determine number of protons

atomic number

atomic weight

average mass of naturally occurring isotopes

mass of one proton

one amu = 1/12 of the carbon-12 atom

(difference between proton and neutron mass is very small, the difference is equal to an electron)

half-life correspond with ____ therefore helps determine ____

stability, the relative proportions of these different isotopes

the relationship between atomic weight, isotopes, and moles

the atomic weight of carbon is 12 amu, which means the average carbon weighs 12 amu (meaning carbon 12 isotope is extremely more abundant than 13 or 14) and one mole of carbon atoms is equal to 12 grams

atomic mass

nearly equal to mass number (slightly less than the number of protons and neutrons in a nucleus)

Ernest Rutherford

experimental evidence that an atom has a dense positively charged nucleus that one accounts for a small portion of the atom's volume (VOLUME)

Max Planck

developed first quantum theory - energy emitted as electromagnetic radiation for matter comes in discrete bundles called quanta (the energy of a quantum is given by the Planck Relation)

Plank Relation

E=h*f

Planck's constant

h, frequency of the radiation (in Planck's relation)

Neils Bohr

electron traveled in a circular orbit around the central proton nucleus, this centripetal force acting on the electron is from the electrostatic force between positive protons and negative electrons (used the work of Rutherford and Planck)

Bohr's use of Planck's constant

placed restrictions on the angular momentum that drove the pathways of electrons (previously pathways were defined by classic physics)

L=(n*h)/2pi

because n is the only variable, the angular momentum can only change in discrete amounts respective to the quantum number

what are the similarities between quantized angular momentum and Planck's concept of quantized energy

There is only discrete energy levels possible, energy isn't infinite

Bohr related the permitted angular momentum values to the energy of the electron to obtain:

the energy of the electron changes in discrete amounts with respect to the quantum number (im sure the actual equation is not important to memorize E=-Rn/n^2)

what is the energy of the electron equation saying? (E=-Rn/n^2)

as the energy of an electron increases, aka becomes less negative, the farther out from the nucleus it will be located (larger n)

important point: while magnitude of the fraction is getting smaller, the actual value it represents is getting larger (becoming less negative)

Rn

Rydberg unit of energy

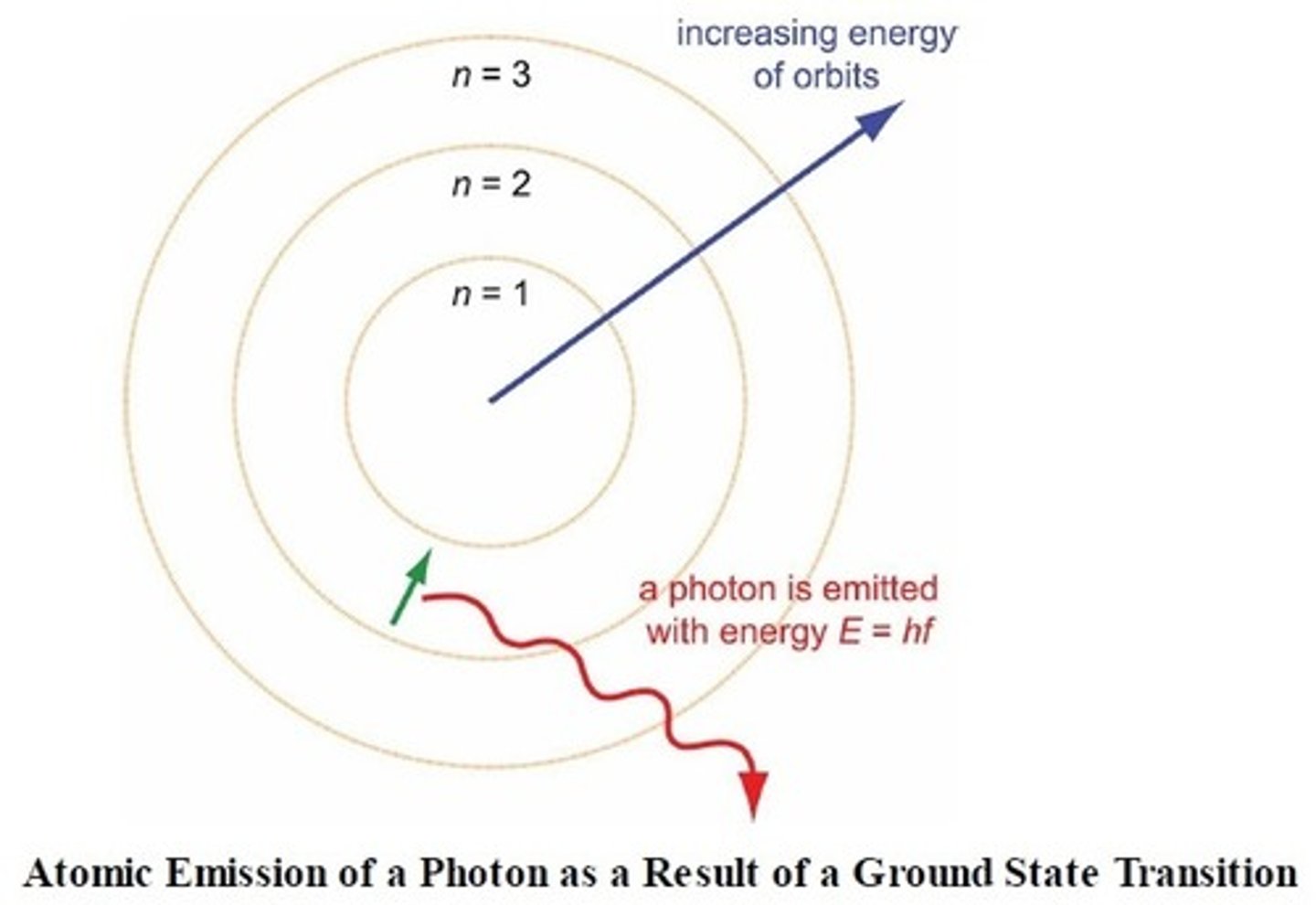
ground state

n=1 (lowest and smallest energy radius)

electron orbit

bohr said that electrons revolved in a defined pathway at a discrete energy value, and that with the transfer of energy (gaining) they could "jump" to higher energy orbits or "fall" with the loss of energy (he likened the electrons orbiting the nucleus the way the planets do with the sun)

excited state

when at least one electron in an atom is at a higher energy level than normal

how was Bohr wrong? why is he important/useful?

important for conceptualization of atomic behavior, but he was wrong because electrons are not restricted to specific pathways, they tend to be localized in certain regions of space. It is still useful for explaining atomic emission and absorption spectra of atoms

all systems tend toward ________ _________

minimal energy (lowest energy = more stability)

atomic emission spectra

E=(h*c)/lamda

h

planck's constant

c

speed of light

lambda

wavelength

when electrons return close to their ground states, they will

emit a photon with a wavelength characteristic of the specific energy transition it undergoes

atomic emission spectrum

each element has unique emissions from when the electrons change energy levels (because they all have distinct energy levels) so that line spectrum can be used as a fingerprint for that element

Lyman series

transition from energy level n=1 to energy level n=2 or higher -- larger energy transitions so shorter photon wavelengths (i dont get that ask doctor nataro page 13)

Balmer series

transition from energy level n=2 to energy level n=3 or higher

Paschen series

transition from energy level n=3 to energy level n=4 or higher

combining Bohr's and Planck's calculations we derive a complex-appearing equation that says

the energy of the emitted photon corresponds to the difference in energy between the higher-energy initial state and lower-energy final state

positive E correlates to _____ and negative E from the equation correlates to _______

emission, absorption

atomic emission versus absorption spectrum

for an element, the wavelengths of the emission and absorption (to "fall" or "jump" and energy level) are the same

each element has a characteristic set of energy levels

atomic absorption spectrum

useful for identifying elements in the gas phase, energy at a specific wavelength absorbed causes an "energy jump"

energy is absorbed for an electron to "jump" levels through ____ and emitted in the same form when they "fall" levels

light

Bohr's model failure

not taking into account the repulsion between multiple electrons surrounding the nucleus (this is why his model failed when explaining the structure and behavior of atoms with more than one electron)

most important difference between Bohr's model and modern quantum mechanical model

Bohr postulated that electrons follow a clearly defined circular pathway, or orbit at a fixed distance from the nucleus

modern: electrons move rapidly and are localized within regions of space around the nucleus called orbitals

the best we can do now (bohr's time thought we could identify the location or pathway of an electron) is more modest:

describe the probability of finding an electron within a given region of space surrounding the nucleus

Heisenberg uncertainty principle

it is impossible to simultaneously determine, with perfect accuracy, the momentum and position of an electron

to determine momentum the electron has to be moving

to determine position the electron must stop (confused by this ask nataro page 16)

any electron in an atom can be completely described by 4 quantum numbers:

n, l ,ml , ms

Pauli exclusion principle

no two electrons in a given atom can possess the same set of four quantum numbers

energy state

position and energy of an electron described by its quantum numbers

the relationship between n, l, ml, ms

the value of n limits the value of l, which in turn limits the value of ml, ms is either +/- 1/2`

principal quantum number (n)

the larger the integer value of n, the higher the energy level and radius of the electron's shell (within each shell there is a capacity to hold a certain number of electrons)

maximum number of electrons within a shell

2n^2

difference in energy levels

the distance between n=1 and n=2 is the largest (when only moving one level) n=3 and n=4 is smaller, this makes sense when you think of 1/(n-i)^2 - 1/(n-f)^2

azimuthal quantum number (l)

shape and number of sub shells within a principle energy level (shell)

important implications for chemical bonding and bond angles

how does n limit l

the values for l are any integers between 0 and n-1 (so there is only one subshell in n=1 --> value of n tells you how many subshells there are)

spectroscopic notation

s (l=0) p (l=1) d (l=2) f (l=3)

if n=4 and l=2 then it is 4d

if n=3 and l=0 then it is 3s

maximum number of electrons within a seubshell

4l + 2 (ask dr. nataro page 18)

magnetic quantum number (ml)

specifies the particular orbital within a sub shell where an electron is most likely to be found at a given moment in time

the possible values are between -1 and +1 (including 0)

possible ml equation

2l+1

for any n, this produces ___ orbitals and a maximum of ____ electrons (two per orbital)

n^2, 2n^2

probability density

likelihood that an electron will be found in a particular region of space

as you go left to right (--->) on the periodic table what happens? (electrons)

an electron is added to the orbital)

spin quantum number (ms)

electron has two spin orientations designated +1/2 and -1/2

paired electrons

whenever two electrons are in the same orbital, they must have opposite spins

parallel spins

electrons in different orbitals with the same ms values

electron configuration (ex: 2p^4)

the pattern by which subshells are filled, as well as the number of electrons within each principal energy level and subshell

aufbau principle (building-up principle)

electrons fill from lower to higher-energy subshells and each subshell will completely fill before electrons begin to enter the next one

n + l rule (important for test day)

the lower the sum of the values of the first and second quantum numbers, the lower the energy of the subshell

if two subshells possess the same n + l value (important for test day)

the subshell with the lower n value has a lower energy and will fill with electrons first

electron configuration of an ion

anion / F-

cation / Fe3+

anion: electrons fill the same way that they normally would

[He]2s^2 2p^6

cation: start with the neutral atom and remove electrons from the subshells with the highest n value first, then electrons are removed from the subshell with the highest l value among these

[Ar]3d^5

In subshells that contain more than one orbitals, the orbital fills in accordance to this rule

Hund's Rule

Hund's Rule (bus rule)

within a given subshell, orbitals are filled such that there are a maximum number of half-filled orbitals with parallel spins (they fill so each has their own orbital before doubling up, like a school bus)

why does hund's rule happen that way?

electron repulsion, electrons in the same orbital are closer to each other so they repel each other more than electrons in separate orbitals

a consequence of Hund's rule is

half-filled and fully filled orbitals have lower energies (higher stability) than other states

the consequence of Hund's rule creates two notable exceptions to electron configurtoin that are often tested on the MCAT:

chromium (and other elements of that group) and copper (and other elements in its group)

3d^4 becomes 3d^5

3d^9 becomes 3d^10

paramagnetic materials

composed of atoms with unpaired electrons that orient their spins in alignment with a magnetic field, so the material is weakly attracted to the magnetic field

PARAmagnetic = magnetic field that causes PARAllel spins in unpaired electrons and therefore cause an attraction

diamagnetic materials

atoms that only have paired electrons will be slightly repelled by a magnetic field

valence electrons for Group IA and IIA

the highest s subshell electrons

valence electrons for Group IIIA through VIIIA (13-18)

the highest s and p subshell electrons

valence electrons for transition elements

in the highest s and d subshells (even though they have different principal quantum numbers)

valence electrons for lanthanide and actinide series

in the highest s and f subshells (even though they have different principal quantum numbers)

how do elements in period three (starting with sodium) and below violet the octet rule? (will be discussed more in chapter 3)

they may accept electrons into their d subshells, which allows them to hold more than eight electrons in their valence shell