AP Physics C: Mechanics Leftovers

Moments of Inertia

For an object orbiting around a center:

• Moment of Inertia is: I = mR²

Most 3D Shapes:

• dm / M = dv / V (mass over volume) (density)

• dm = ( M / V ) dv

Most 2D Shapes:

• dm / M = dA / A (mass over area)

• dm = ( M / A ) dA

Rigid Rod:

• dm / M = dl / L (mass over length)

• dm = ( M / L ) dl

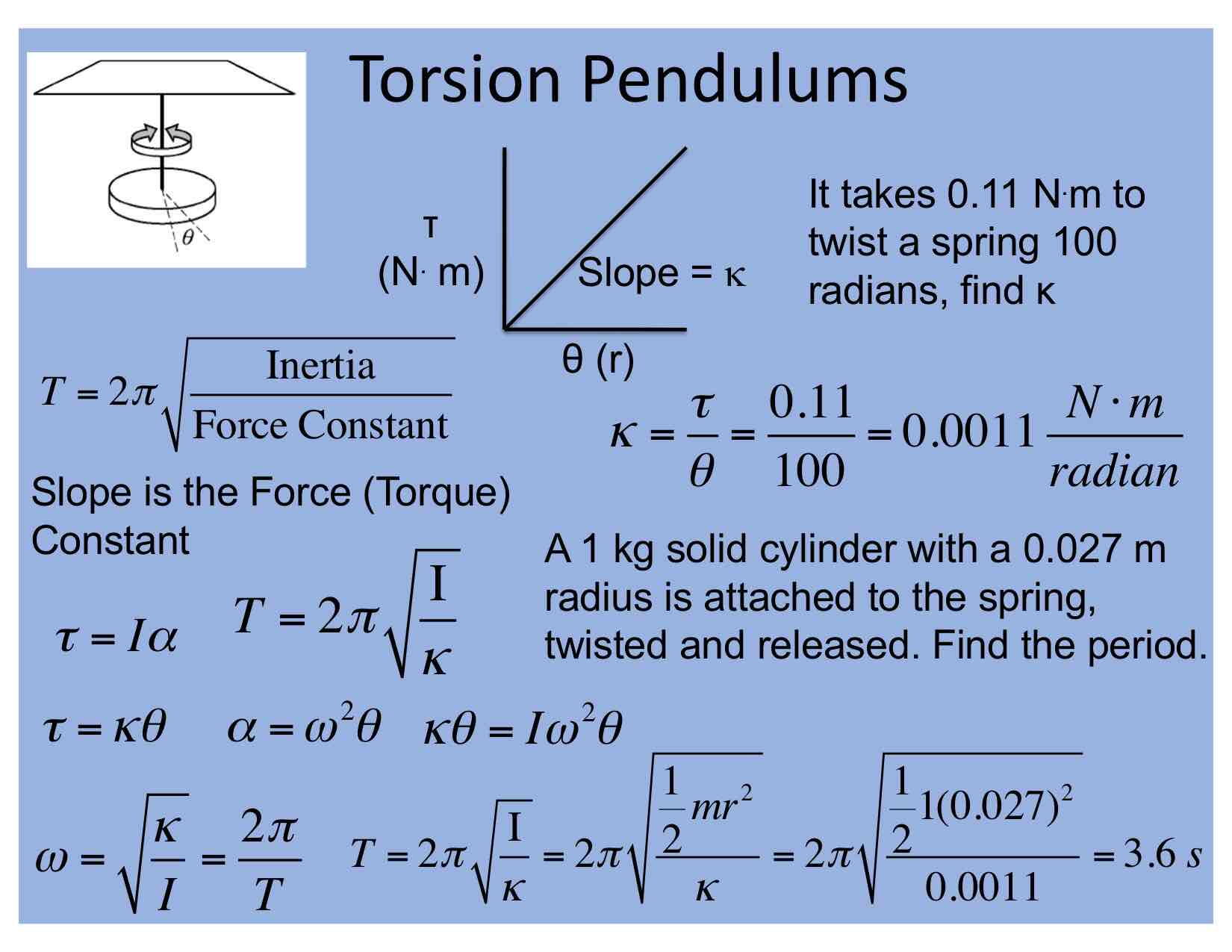
Torsion Pendulum

Vertical Circular Motion

At the top of the circle:

• F_c = F_g + T

At the bottom of the circle:

• F_c = T - F_g

Center of Mass

* you can do center of velocity (it’s the same thing) (REMEMBER DIRECTION)

Person Standing on an Elevator (Scale Reading)

Potential Energy

When graph looks like sinx or cosx:

• object’s position will oscillate because KE changes from positive to negative

• this means that the object will move forward, then turn around, move back, turn back around, and continue this process

Work

Net Work is 0 when force is CONSTANT

Work is the negative of U

Acceleration in Rotation Kinematics

Not constant because there is a pulley that rotates, making various angles all while the mass rises and falls

Normal Force

Always away from the surface

Spring + Tension

Net torque = Torque of Spring - Torque of Tension

Angular Problems

Angle of a Pulley

• means arclength

• use bridge equation

USE TORQUE WHEN ANGULAR

Possible Errors

Anything that is assumed:

• masses

• whether friction is negligible or not

Free Body Diagram (Centripetal)

Centripetal -

• should never be drawn in free body diagram

• should use Tension and Gravity to depict Centripetal

• When there is centripetal

  • Force is NET INWARD (INWARD force is greater) F_c = F_in - F_out

Tension & Contact Force

Contact Force

• Force in the opposite direction of the acceleration of the system

• Usually denoted by F_2,1

• Steps:

  • find acceleration of the system based on given force and mass values

  • multiply the acceleration of the system by the force MAKING the contact force (in the case above, F₂)

  • Shortcut:

    • F_2,1 = [ m₂ / (m₁ + m₂) ] * F_A

    • If there are more masses, just divide by total mass

Tension

• directed away from ‘gravity’

Series of Springs → Series of Strings

Series of springs can be seen as a series of strings when doing a problem

• the Tension from the Strings is EQUAL to the Force of the Spring from the Springs

Period of a Spring (T)

Period (T) can be split up into components of max compression, equilibrium, and max stretch because the spring oscillates

T_total = T_{max compression} + T_equilibrium + T_{max stretch} + T_equilibrium

When solving for T of one part just do (1/4)T_total

Use it on the period for mass spring mechanisms

Angular Momentum

Conservation of Energy

For All Oscillating Systems

• K_max occurs at equilibrium

• U_max occurs at end point

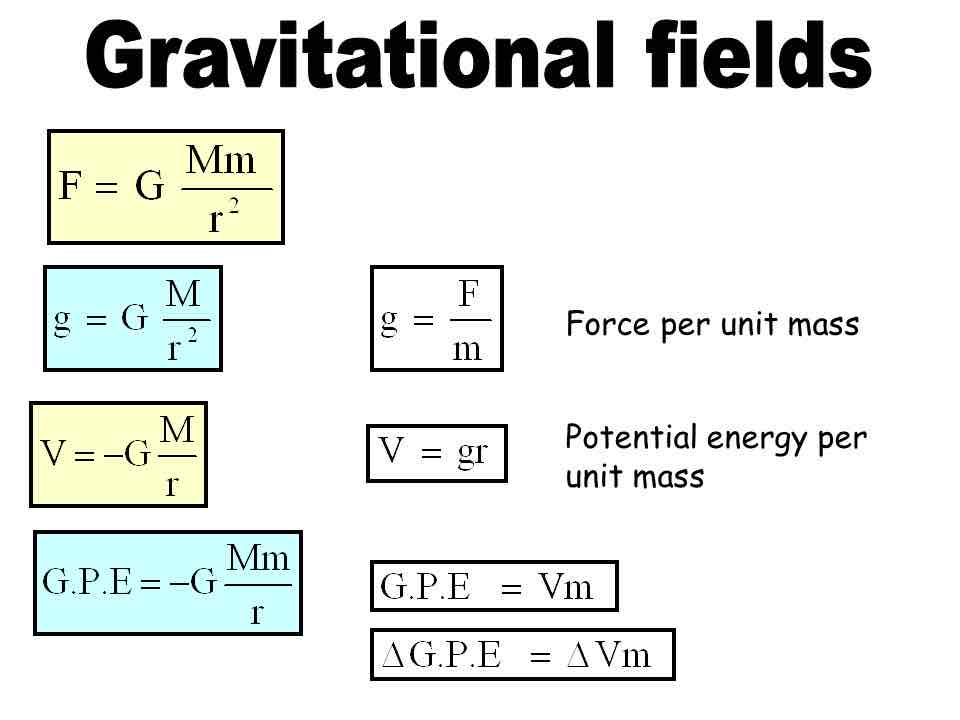
Gravitation Stuff

v = sqrt(GM / R)

Escape Speed

GPE = KE

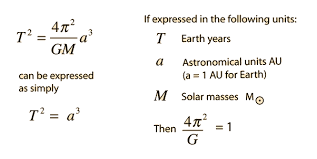
Kepler’s Third Law

Series & Parallel Springs

Series:

• keff = k1 + k2 + …

Parallel:

• 1/keff = 1/k1 + 1/k2 + …

Equation for SHM

y = A sin (wt + 0）

Rotational Forces (Energy)

Rolling With Slipping

• Kinetic friction present

• Contact point: there is motion so not 0

Rolling Without Slipping

• Static friction present

• Velocity at the contact point is 0

• Velocity of the center of mass = r w

• KE = KEt + KEr

Slipping

• pure translational motion

• no friction

*smaller the moment of inertia, faster the object

Torque

Torque

• increases when R increases

• is ZERO when at the pivot point

• Account for NET torque

• Torque = integral( I * w )

• NET TORQUE = 0 when in constant angular speed

*component of FORCE must be PERPENDICULAR to AXIS OF ROTATION

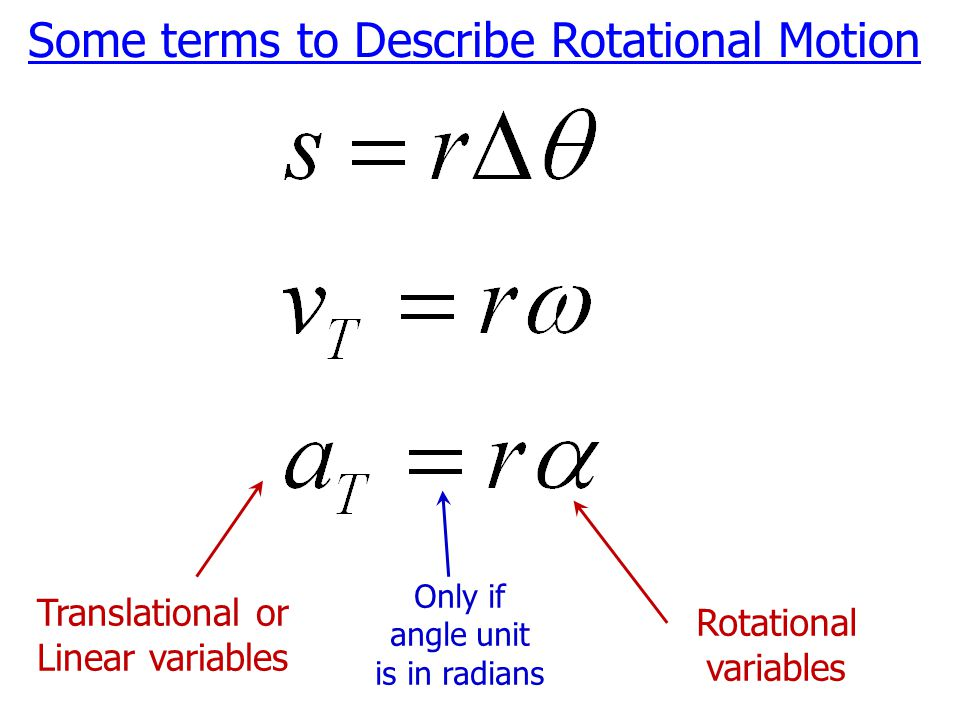
Bridge Equations

Impulse

When something bounces higher, larger impulse

Graph:

• will look like absolute value function

• impulse will reach a max and then go back to 0 because it is only exerted when contact is made

*cannot know unless u have time of contact

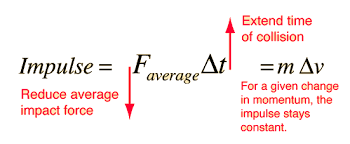
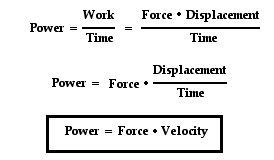
Power

Energy & Work

Gravitational Force

Writing Differential Equations

just make sure that you have a d/dt somewhere

Example:

Requisite from problem: F = βv² (resistive force)

F_net = ma → -βv² = ma → -βv² = m (dv/dt)

*Remember how to do Integration By Parts

Graphing x, v, a for FRQs

When there is a resistive force

• position (x) increases but then levels off because acceleration is negative meaning that velocity is decreasing by time (like a square root curve)

• velocity (v) starts at max but then decreases drastically then levels off to 0 since acceleration is negative (live a 1/x graph)

• acceleration (a) is max in the negatives but then increases slowly and levels off to almost 0 when the resistive force equation looks something like this ( F = βv²) since velocity is directly proportional with acceleration

Rod (Center of Mass)

Center of Mass

• located in the center of the rod

• when using conservation of energy for ROTATION, use L/2 as the height for U_^g

Conservation of Energy vs. Conservation of Momentum

Conservation of Energy

• use when prompted with “just before the object hits other object”

• use when object starts from higher place and then you need to find max compression of spring or velocity

• TOTAL ENERGY (gravitational)

  • E = -(1/2) GMm/r

Conservation of Momentum

• use when there is a COLLISION

When asking for velocity or angular velocity

use kinematics

Identical Disks

I = (number of disks) * I_{each disk}

Momentum

• MOMENTUM is ALWAYS conserved

• KINETIC ENERGY is ONLY conserved in a PERFECTLY ELASTIC collision (so it may or may not be conserved)

• explosions - momentum is conserved because it is an internal system

Springs

v_max → when spring is at equilibrium

a_max → when spring is at maxcompression or max stretch

equilibrium is ALWAYS half the position of the AMPLITUDE

Free fall

When dropping an object from a plane and then a second object a second later:

• vertical distance between the two objects is constantly increasing even though acceleration is the same

• this is because there is acceleration so velocity changes at a constant rate but then distance changes at an exponential rate

Period of Pendulum & Angle

Period is not affected by angle as long as angle is SMALL

Vacuum

means that there is no air drag force or air resistance

AT free fall

Terminal Velocity

Before reaching Terminal Velocity,

• there is still acceleration downwards