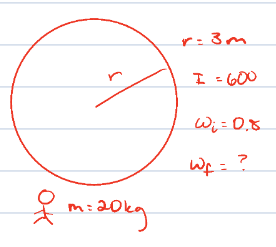Chapter 11: Rotational Dynamics & Static Equilibrium

Torque

• The ability of a force F to rotate the body around an axis

  • depends on the magnitude of its tangential component F_t and the distance the Force is applied ( r )

• Torque = τ = (F)rsin(θ)

  • r: distance from rotational axis

  • F: force

  • θ: angle between F & r

  • unit: Newton-meters Nm

• Torque is a vector

If r is larger, torque is…

larger

Newton’s Law of Rotation

• Found from Newton’s Second Law

  • F_t = ma_t

  • τ = F_tr = ma_tr

  • τ = m(αr)r = (mr²)α

  • τ = Iα

• For more than one force, we can generalize: τ_net = Iα in radians

The torque due to the tangential component of force causes…

an angular acceleration around the rotation axis

If the turning tendency of the force is counterclockwise, the torque will be…

positive

If the turning tendency of the force is clockwise, the torque will be…

negative

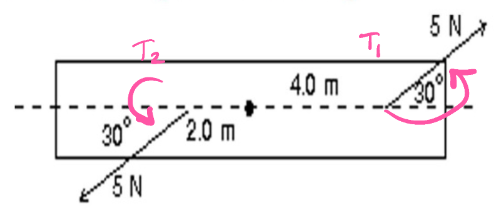
A rod is pivoted about its center. A 5-N force is applied 4 m from the pivot and another 5-N force is applied 2 m from the pivot, as shown. The magnitude of the total torque about the pivot (in N*m) is?

• F₁ = 5 N

• r₁ = 4 m

• F₂ = 5 N

• r₂ = 2 m

• τ₁ = Frsin(theta) = (5 N)(4 m)(sin(30)) = 10

  • counterclockwise → +10

• τ₂ = Frsin(theta) = (5 N)(2 m)(sin(30)) = 5

  • counterclockwise → +5

• τ₁ + τ₂ = τ = 15 N*m

Equilibrium & Torque: Conditions

1. The net external force must be zero at equilibrium

• ∑F = 0

• OR ∑F_x = 0 & ∑F_y = 0

• translational equilibrium → no translational motion

  • no sliding, no accelerating

• a = 0

• v = constant or = 0

2. The net external torque must be zero at equilibrium

• ∑τ = 0

• rotational equilibrium → no rotational motion

  • no spinning, no rotating

• α = 0

  • no angular acceleration

• ω = constant or = 0

  • spinning at constant rate or not spinning at all

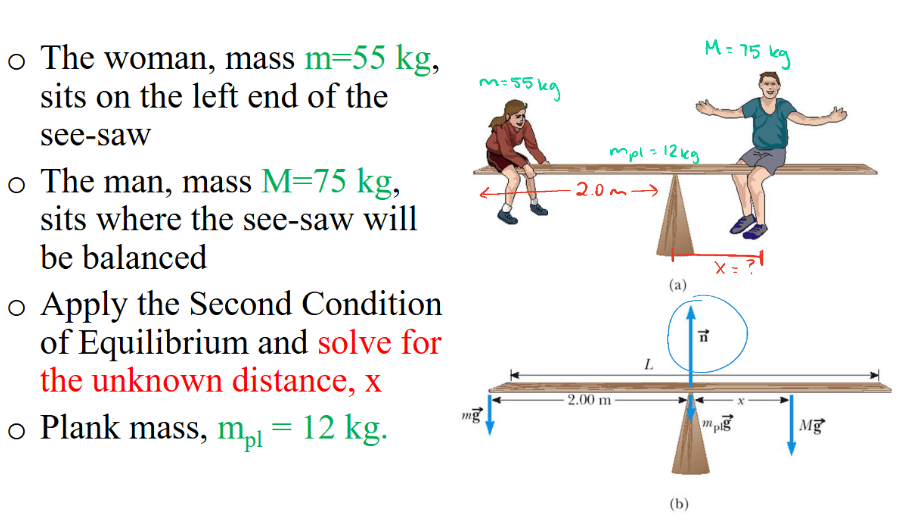
• ∑τ = 0

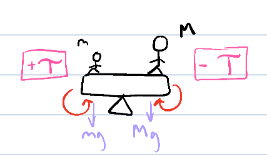
• m = 55 kg

• M = 75 kg

• m_pl = 12 kg

• d = 2.0 m

• x = ?

• ∑τ = 0

• τ = Frsin(theta)

  • F = mg

  • mg *r *1

• τ_mg = +mg(2.0m) - Mg(x) + n(0) - m_plg(0)

  • mg → cc → positive

  • Mg → clockwise → negative

  • n → r = 0 b/c r is distance from pivot point

  • m_pl → r = 0

• τ_mg = +mg(2.0m) - Mg(x)

• τ_mg = (55 kg)(2.0 m) - (75 kg)(x)

• x = 15 m

r is the distance from the…

pivot point

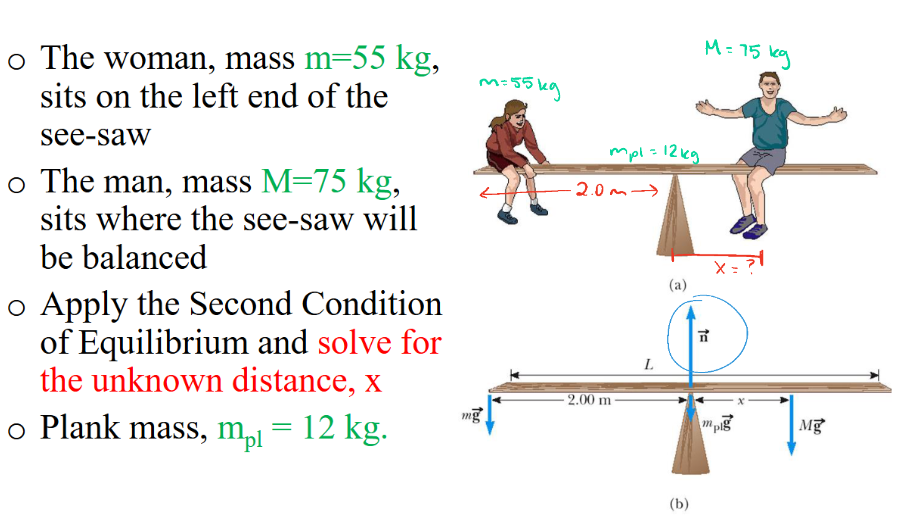
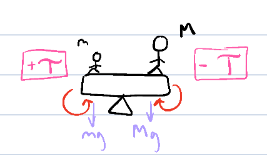
If we do the Lady as the pivot point…

• ∑τ = 0

• τ = Frsin(theta)

  • F = mg

  • mg *r *1

• τ_mg = mg(0m) - Mg(2+x) + n(2) - m_plg(2)

  • mg → r = 0 b/c r is distance from pivot point

  • Mg → clockwise → negative; distance 2+x from pp

  • n → r = 2 b/c r is distance from pp

    • the n is positive because it is an upward acting force, counterclockwise lifing board on right

  • m_pl → r = 2; clockwise → negative

• τ_mg = -(75 kg)(2+x) + 2n - (12 kg)(2)

Angular Momentum

• rotational equivalent of linear momentum

• L = Iω

  • kg*m²/s

  • I: Moment of Inertia

    • how spread out your mass is

  • ω: angular velocity

    • spin speed

• ∑τ = ΔL/Δt

• L = (mv²)/ω

Conservation of Angular Momentum

• If the net external torque acting on a system is 0, the angular momentum L of the system remains constant, no matter what changes take place within the system

• L_i = L_f in an isolated system

  • rotational

  • linear: p_i = p_f

• I_iω_i = I_fω_f

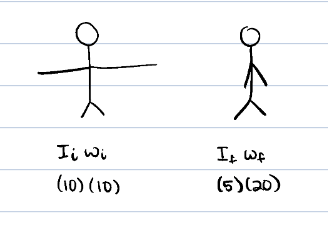
Which is faster?

• I_iω_i = I_fω_f

  • If no external torques act

  • angular momentum remains constant

• 1: I increases, ω must decrease

• 2: I decreases, ω must increase

• So, she is faster in the second position

More condensed space typically equals…

an increased angular velocity due to conservation of angular momentum.

Rotational Work & Power

• a torque acting through an angular displacement does work, just as a force acting through a distance does

• W = τΔθ

• Power is the rate at which work is done, for rotational motion and translational motion

• P = W/Δt = τ(Δθ/Δt) = τω

A playground merry-go-round has a radius of 3.0 m and a rotational inertia of 600 kg × m². It is initially spinning at 0.80 rad/s when a 20-kg child crawls from the center to the rim. When the child reaches the rim, the angular velocity of the merry-go-round is what?

• r = 3.0 m

• I = 600 kg*m²

• ω_i = 0.80 rad/s

• m = 20 kg

• ω_f = ?

• I_iω_i = I_fω_f

• (600 kg*m²)(0.80 rad/s) = (600 + mr²)(ω_f)

• 480 = (600 + (20 kg*3.0²))(ω_f)

• ω_f = 0.62 rad/s