2nd- Chapter 4 The sample Correlation Coefficient.

Rxy

The sample correlation coefficient.

Book Def: measures the strength of the linear relationship between X and Y. It gives the average change in standard deviations of Y for every 1 standard deviation increase in X.

Ex: rxy= +0.72 means that the Y-variable rose an average of 0.72 std deviations for every 1 std deviation increase in X.

Gpt:

• A number that measures how strong and what direction the relationship between X and Y is.

• It always falls between –1 and +1.

  • +1 = Perfect positive relationship (X goes up, Y goes up exactly).

  • –1 = Perfect negative relationship (X goes up, Y goes down exactly).

  • 0 = No linear relationship.

• Interpretation:
  rₓᵧ = +0.72 → On average, for every 1 standard deviation increase in X, Y increases by 0.72 standard deviations.

• Example:

  • X = Hours studied, Y = Exam scores

  • rₓᵧ = 0.72 → Strong positive relationship (more hours, higher scores).

(The sample correlation coefficient) rxy  equation:

Book Def:

Think of (yi-y ̅) as Y’s deviation of the mean and (xi-x ̅ ) as X’s deviation from the mean.

(yi-y ̅)(xi-x ̅) is the product of Y’s deviation from its mean and X’s deviation from its mean.

∑(yi-y ̅)^2 and ∑(xi-x ̅)^2 are the total variation of X and Y.

Gpt: 

The formula measures how strongly two things (X and Y) move together.

• If both go up and down together, the correlation is positive (close to +1).

• If one goes up when the other goes down, the correlation is negative (close to –1).

• If they move randomly, the correlation is near 0.

Part	Meaning	In simple words
xi​	Each value of X	One data point for X
yi	Each value of Y	One data point for Y
xˉ	Mean (average) of all X’s	The center of X values
yˉ	Mean (average) of all Y’s	The center of Y values
)(xi​−xˉ)	X’s deviation from its mean	How far each X is from average
(yi​−yˉ​)	Y’s deviation from its mean	How far each Y is from average
Numerator ∑(xi−xˉ)(yi−yˉ)\	Sum of products of deviations	Shows how X and Y move together
Denominator Squared ∑(xi−xˉ)² ∑(yi−yˉ)²	Scale adjustment	Makes result between –1 and +1

1. See how far each X and Y is from their average.

2. Multiply those differences together for each pair.

   • If both are above or below average → positive product.

   • If one is above and the other below → negative product.

3. Add up all those products.

4. Divide by the total variation (the denominator).

5. The result tells you how related X and Y are.

Example intuition

• r=  +1: Perfect upward trend — when X increases, Y always increases.

• r= −1: Perfect downward trend — when X increases, Y always decreases.

• r= 0r: No consistent relationship between X and Y.

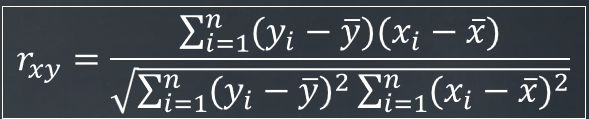
Y=

Bood Def:

Dependent Variable/ output

-What you’re trying to explain, predict, or measure. 

-Think of it as the “outcome or result” 

Ex: 

Y= House price 

Y= Infant mortality rate

Y= Exam score 

Y is the Dependent Variable because it should somewhat depend on the model.

Gpt: 

Y (Dependent Variable): the thing that changes as a result.
→ It “depends” on X.

In short

• X → given or controlled → causes changes in Y.

• Y → responds → depends on X.

• X is “independent” not because it’s totally separate from Y in real life,
  but because we treat it as something that isn’t affected by Y in our model.

X=

Independent Variable/ input/ determined independently.

-The factor you think influences or explain Y. 

Ex:

X= Study time (affects exam score)

X= Income per person (Affects infant mortality rate)

X=Square per footage of a house (affects price)

X is the Independent Variable, NOT because it’s independent of Y, but because it should determined outside of the model, called exogeneity.

Gpt: 

X (Independent Variable): the thing we control or choose to see how it affects Y.
→ It’s “independent” because it’s decided outside the system we’re studying.

In short

• X → given or controlled → causes changes in Y.

• Y → responds → depends on X.

• X is “independent” not because it’s totally separate from Y in real life,
  but because we treat it as something that isn’t affected by Y in our model.

X & Y Examples:

Let’s say we’re studying:

X = hours studied
Y = exam score

• Your exam score (Y) depends on how much you study (X).

• You choose how many hours to study — that’s outside the exam system.
  That’s why X is independent.

• The exam score responds to how much you studied — that’s why Y is dependent.

Example 1

Y = Exam Scores

X = Mystatlab Averages

Example 2

Y = Infant Mortality Rates

X = Income per Capita

Example 3

Y = Sale Price of a Residential Home

X = Square Feet of Interior Space

Example 4

Y = Exam Scores

X = Student ID number (qualitative data, lol)

What we’re trying to figure out: 

How strong is the relationship between X and Y? In what direction? How much evidence is there that X and Y are actually related?