CPSC 223 Midterm 2 Study Guide: TDD and BSTs

six components of a specification in TDD

Purpose, Assumptions, Inputs, Outputs, State Changes, Cases and Expected Behavior

four phases of a test in TDD

Write test, run test (fail), write code, run test (pass)

five steps to the TDD cycle

1. Write test to spec, 2. Run and fail, 3. Write code, 4. Run and pass, 5. Refactor

definition of a tree

A connected undirected graph with exactly one path between any two vertices

definition of a forest

An undirected graph where between any two vertices there is at most one path

polytree

A connected directed graph with exactly one undirected path between any two vertices

polyforest

A directed graph where between any two vertices there is at most one undirected path

set-based notation for a graph

G = (V, E), where V is vertices and E is edges

degree of a node

The number of edges connected to it

parent and a child in a BST

A parent is a node with children; a child is a node linked below another

organizing structure of a BST

Left child < parent < right child

nodes with no children

Leaf nodes

node at the top of a tree

Root

nodes with children

Internal nodes

subtree

A tree structure rooted at a child of another node

path in a tree

A sequence from the root to a leaf

advantage of having two children

Better balance and faster searching (tree is more compact)

best-case BST vs. worst-case BST

Best-case: balanced; Worst-case: linear like a linked list

case tree results from inserting in order

Worst-case (linked list shape)

insertion order for the most efficient BST

In an order that balances the tree (e.g. median first)

cases for BST deletion

Node has no children, one child, or two children (use in-order successor)

three traversal methods of a BST

In-order, Pre-order, Post-order

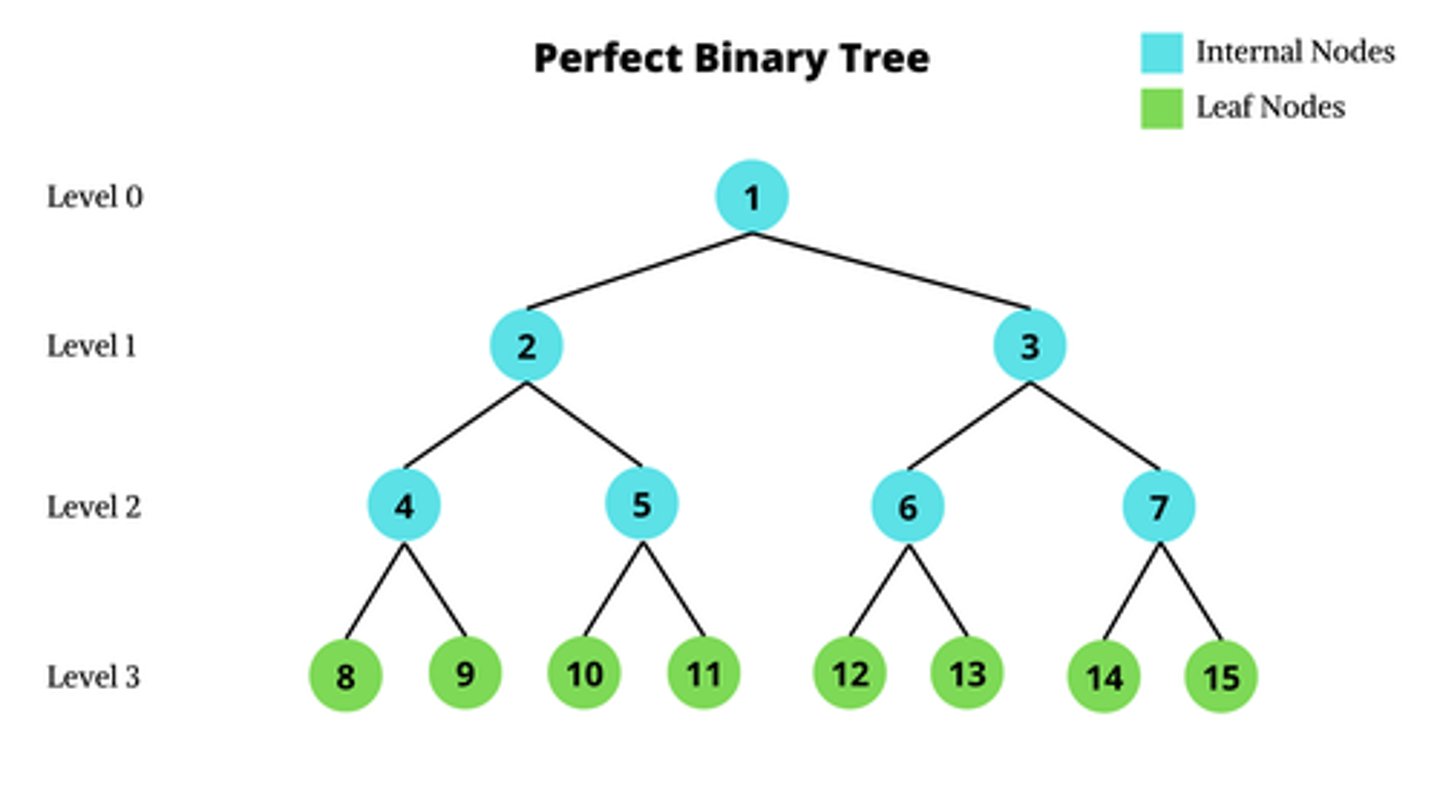
perfect BST

All levels are completely filled

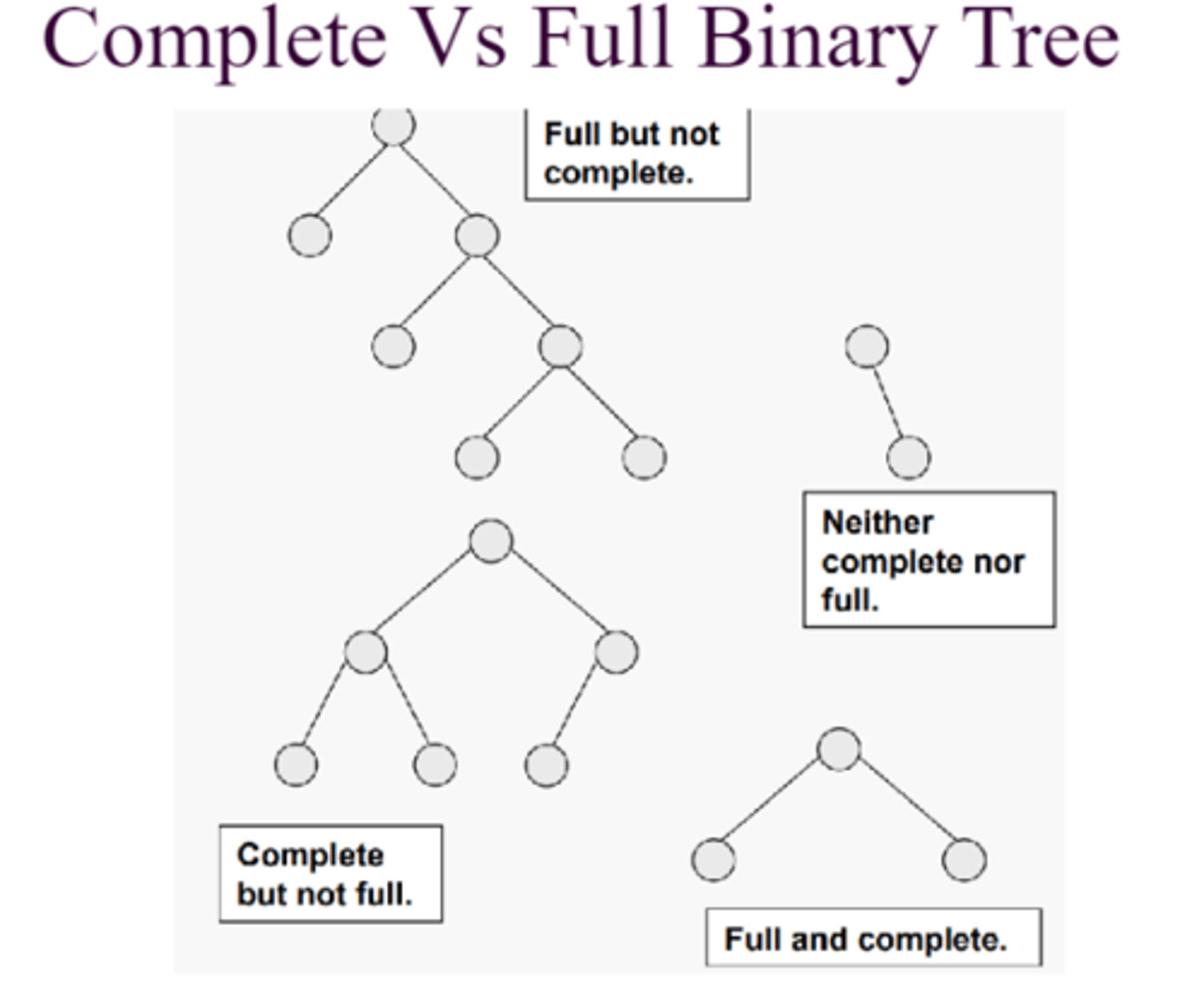
complete BST

All levels are filled except possibly the last, which is filled left to right

insertion order for a perfect BST with 7 nodes

4, 2, 1, 3, 6, 5, 7

in-order successor

The next node in in-order traversal (smallest in right subtree); used in deletion

balance factor in an AVL tree

Height(left subtree) - Height(right subtree)

four AVL rotation types

Left-Left, Right-Right, Left-Right, Right-Left

time complexity of rebalancing a tree via reinsertion

O(n) - because all nodes are visited and reinserted