High School Math Quick Recall and Written Assessments (2015-2020) Vocab and Formulas, Academic Team Math

Weak Spots for me

1.Integrals, differentials, derivatives etc. 2. Probabilities and bell curves. 3. Ellipses and hyperbolas

distance from a line to a point formula

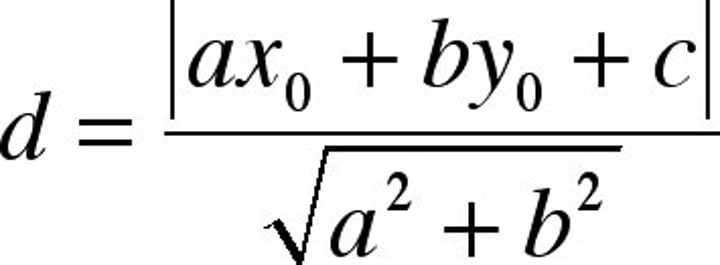
Roots of a cubic equation

Let ax3 + bx2 + cx + d = 0 be any cubic equation and α, β and γ be the roots.

α + β + γ = -b/a

αβ + βγ + γ α = c/a

αβγ = -d/a

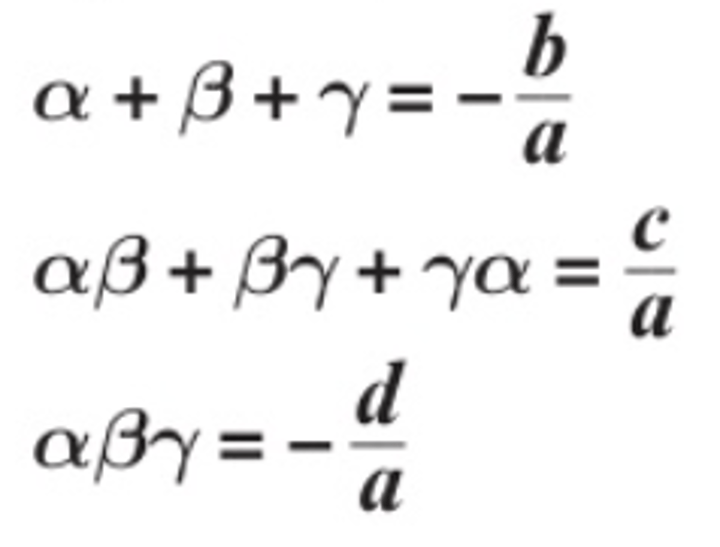
Bell curve rules

1,2,3 stand deviations above mean correspond to 84.1st, 97.7th, and 99.9th percentiles. 1,2,3 below mean correspond to 15.9th, 2.3rd, and 0.1st percentiles

Finding percentile rank of a distribution

Calculate the rank to use for the percentile. Use: rank = p(n+1), where p = the percentile and n = the sample size. For our example, to find the rank for the 70th percentile, we take 0.7*(11 + 1) = 8.4.

If the rank in step 1 is an integer, find the data value that corresponds to that rank and use it for the percentile.

If the rank is not an integer, you need to interpolate between the two closest observations. For our example, 8.4 falls between 8 and 9, which corresponds to the data values of 35 and 40.

Take the difference between these two observations and multiply it by the fractional portion of the rank. For our example, this is: (40 - 35)0.4 = 2.

Take the lower-ranked value in step 3 and add the value from step 4 to obtain the interpolated value for the percentile. For our example, that value is 35 + 2 = 37.

z-value

the number of standard deviations that a point is away from the mean

Z-value formula

(x-mean)/standard deviation

standard deviation formula

sqrt(sum of squares of the deviation from the mean/n-1). ALSO, standard deviation/sqrt(sampel size)=new standard deviation

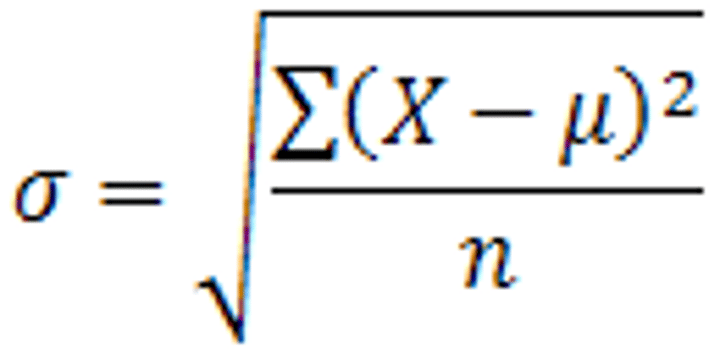
Order doesn't matter

Take factorial, then DIVIDE by other factorial

Order Does Matter

Take Factorial

confidence interval

statistical range, with a given probability, that takes random error into account

margin of error

Find the mean, then see how far is the min. or max., that is your margin

radians to degrees; degrees to radians

180/π; pi/180

radians

the SI unit of measurement of the size of an angle. A complete circle is 2π radians.

least squares regression line

the line that makes the sum of the squared residuals as small as possible

Ex. 3+2.5x; if X increases by 2, then plug into slope to get Y (5) for least-squares regression line

Y=5

coeficient of determination

The most common interpretation of the coefficient of determination is how well the regression model fits the observed data. Usually in a percentage

How to find correlation coefficient from coefficient of determination

(Correlation coefficient)^2 = (coefficient of determination)^2

Angular speed

the rate at which a body rotates about an axis, usually expressed in radians per second (in radians or degrees)

Linear speed

distance traveled per unit of time (in radians or with pi)

Euler's formula

F+V-E=2

rule for tangent + secant

n/a

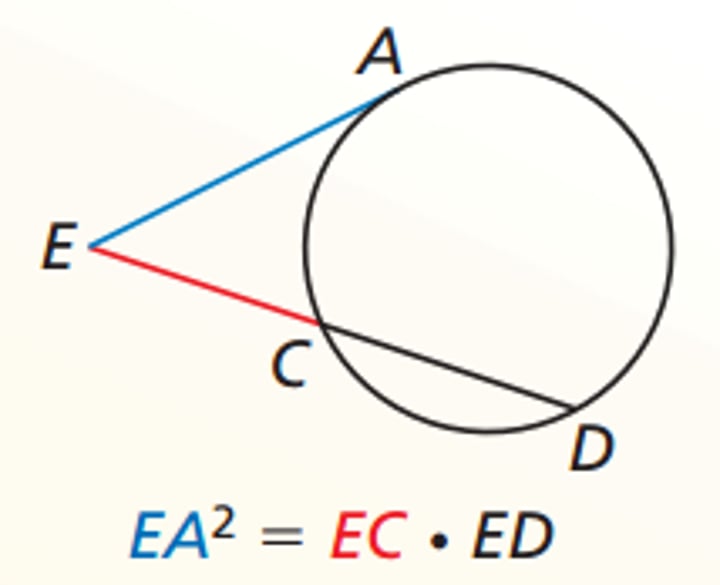
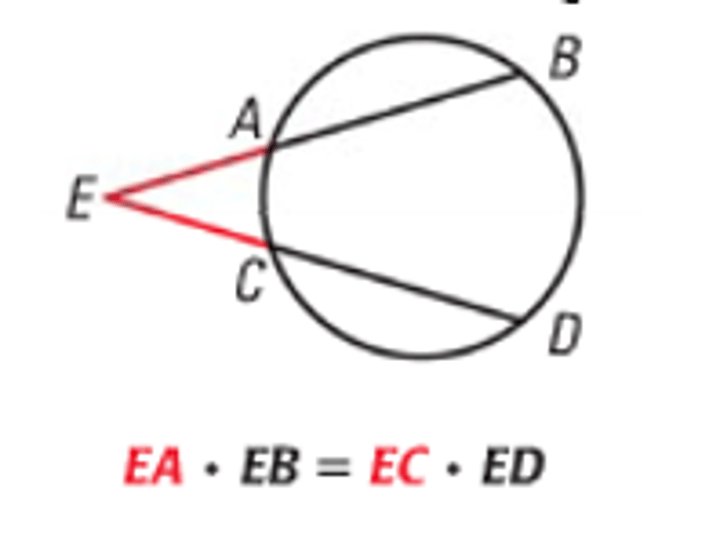
Secant lines length rule

(ab)b=(cd)d

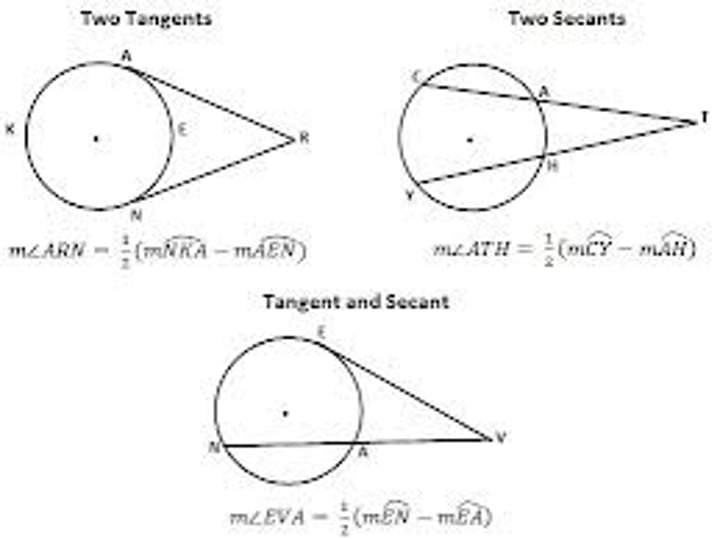
All angle rules involving secants/tangents

(x-y)/2

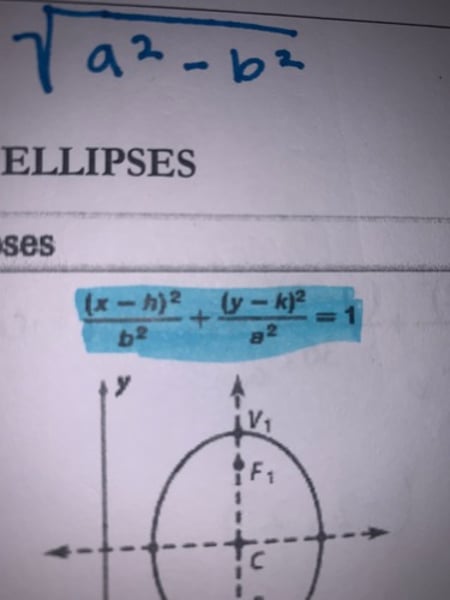
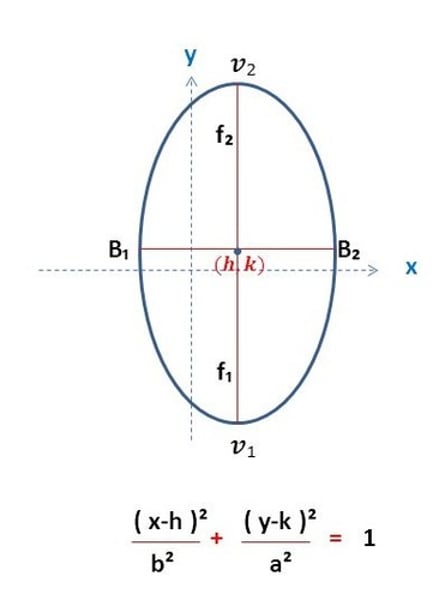
Equation for Ellipse

(x-h)^2/a^2 + (y-k)^2/b^2 = 1

Major and minor Axis of Ellipse

the line that contains the foci and the shorter line that does not, respectively

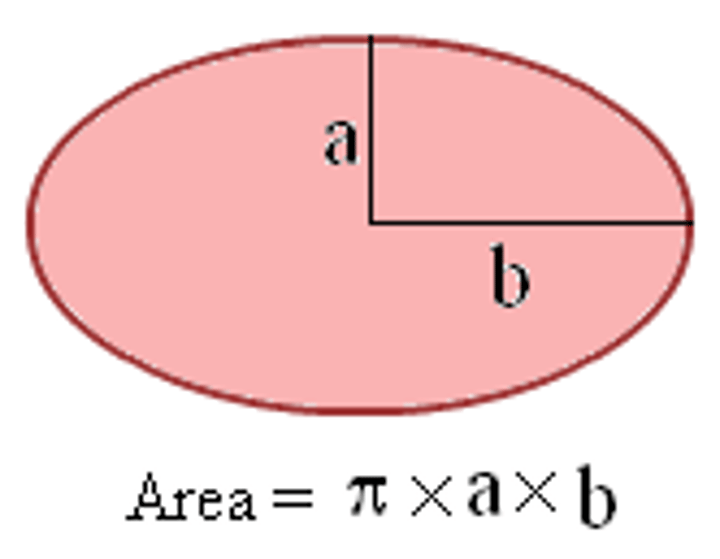
Area of ellipse formula

A=πab

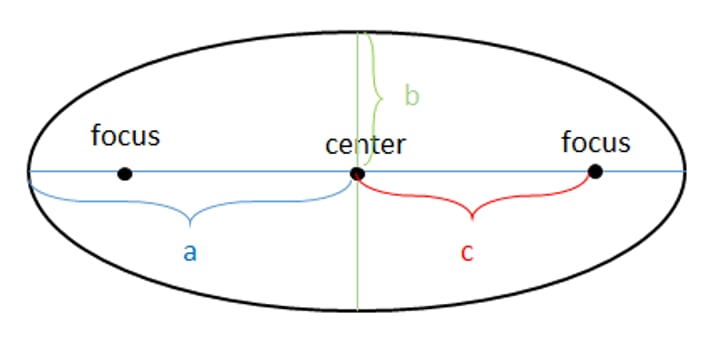
foci of an ellipse

c^2=a^2-b^2

Equation for Hyperbola

x^2/a^2 - y^2/b^2 = 1]

Eccentricity of hyperbola and ellipse

e = √(a2+b2)/a

Other stuff for ellipse and hyperbola

One vertex is at (a, 0), and the other is at (−a, 0)

The asymptotes are the straight lines:

y = (b/a)x

y = −(b/a)x

(Note: the equation is similar to the equation of the ellipse: x2/a2 + y2/b2 = 1, except for a "−" instead of a "+")

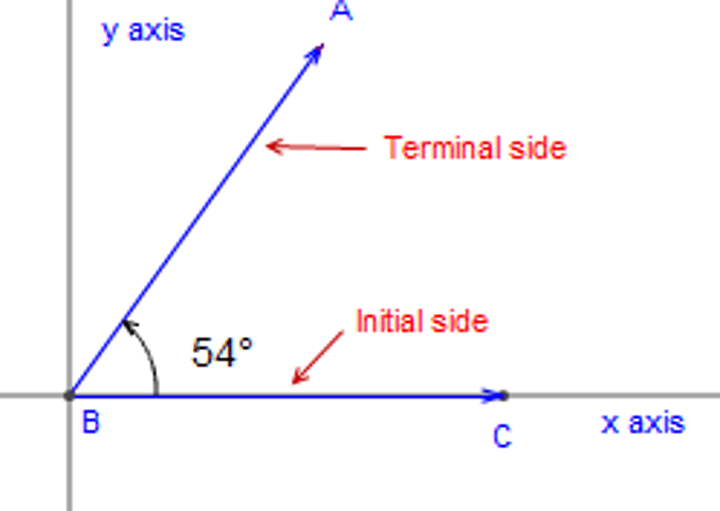
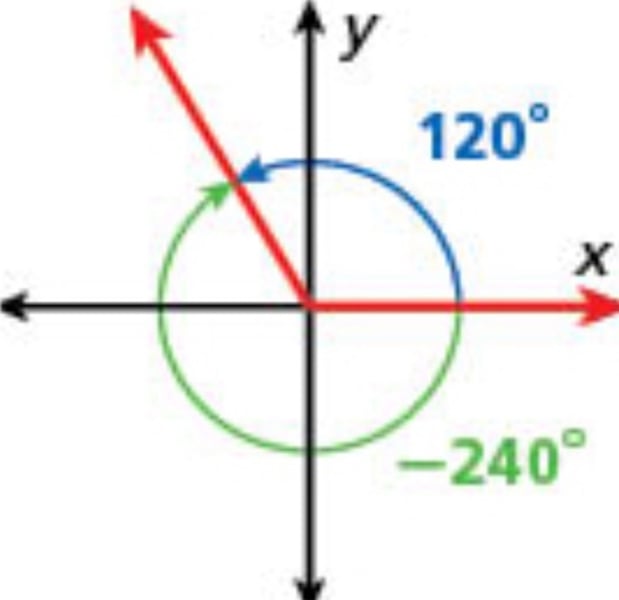
Terminal side of an angle

the ray rotated from the initial side to the endpoint of an angle in standard position

coterminal angles

angles that have the same initial and terminal sides. (opposites). Can find in radians by subtracting 2pi (360 degrees) with the angle.

horizontal tangent line

f'(x)=0; find by finding first derivative of each factor, then set to zero

Derivatives

The slope of any given point in a function

Integral vs derivatives

Integrals are like the "antiderivatives" and are opposite of them. Used to find area.

Integration Rules

To find area of figures - Constant ∫a dx becomes ax + C Variable ∫x dxx2/2 + C

Square∫x2 dxx3/3 + C

Reciprocal∫(1/x) dxln|x| + C

Exponential∫ex dxex + C ∫ax dxax/ln(a) + C ∫ln(x) dxx ln(x) − x + C

Trigonometry (x in radians)∫cos(x) dxsin(x) + C

∫sin(x) dx-cos(x) + C

∫sec2(x) dxtan(x) + C

Multiplication by constant ∫cf(x) dxc∫f(x) dx

Power Rule (n≠−1)∫xn dxxn+1n+1 + C

Sum Rule∫(f + g) dx∫f dx + ∫g dx

Difference Rule∫(f - g) dx∫f dx - ∫g dx

Integration by Parts

Integration by Substitution

Derivative rules

Common FunctionsFunctionDerivative

Constant c to 0

Line x to 1

ax to a

Squarex^2 to2x

Square Root√x (½)x^-½

Exponential e^x to ex

a^x to ln(a) a^x

Logarithms ln(x) to 1/x loga(x) to 1 / (x ln(a))

Trigonometry (x is in radians)sin(x)to cos(x)

cos(x)to −sin(x) tan(x)to sec2(x)

Inverse Trigonometrysin-1(x)to 1/√(1−x2) cos-1(x)to−1/√(1−x2) tan-1(x)to1/(1+x2

finding a definite integral

Use rules of integration to convert the derivatives to integrals, then subtract the plugged in upper-bound with the lower-bound

vectors

quantities that have both a magnitude and a direction

dot product

A form of vector multiplication, where two vectors are multiplied to produce a scalar. The dot product of two vectors, A and B, is expressed by the equation A · B = AB cosx .

magnitude of a vector

AB is the distance from the initial point A to the terminal point B, and is written |AB|. Square and add all lengths of vector, then sqrt it

vector form to unit vector

Ex. 4, -3 = 4/5, -3/5. (Make right triangle)

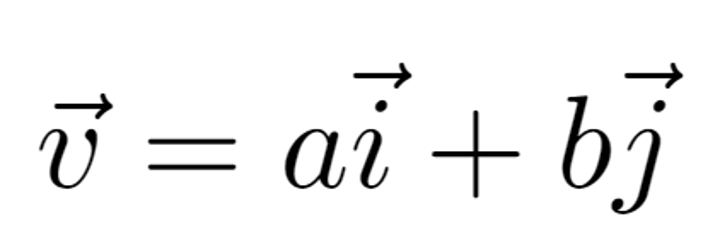
cross-product method of vectors

Make a 3 3 Matrix with the variables on top and respective components on next two rows. Then create three 22 matrices and find determinants. I det. -J det.+ K det. = answer

Common Functions

Function Integral

Constant

∫a dx ax + C

Variable

∫x dx x^2/2 + C

Square

∫x^2 dx x^3/3 + C

Reciprocal

∫(1/x) dx ln|x| + C

Exponential

∫ln(x) dx x ln(x) − x + C

Trigonometry (x in radians)

N/A

∫cos(x) dx

sin(x) + C

∫sin(x) dx

-cos(x) + C

∫sec2(x) dx

tan(x) + C

Multiplication by constant

∫cf(x) dx c∫f(x) dx

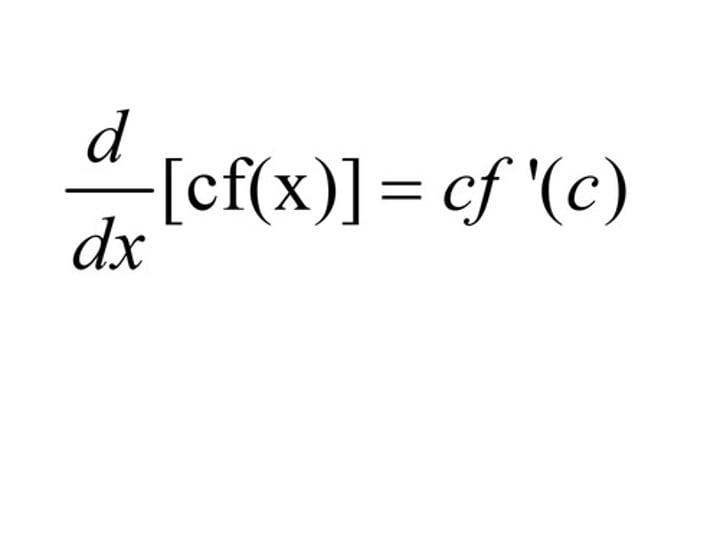
Power Rule

(n≠−1) ∫x^n dx (x^n+1/n+1) + C

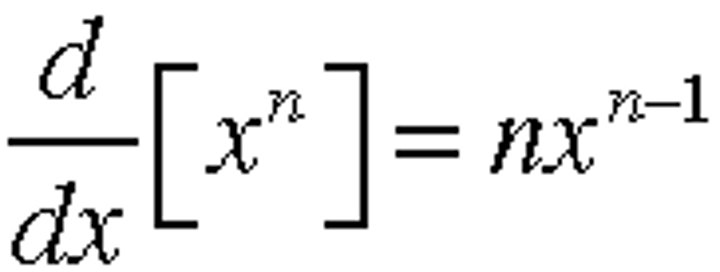
Chain Rule

f'(g(x))g'(x)

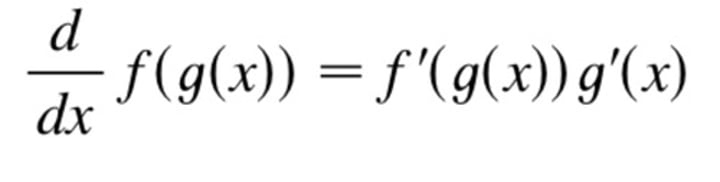
Sum Rule

∫(f + g) dx ∫f dx + ∫g dx

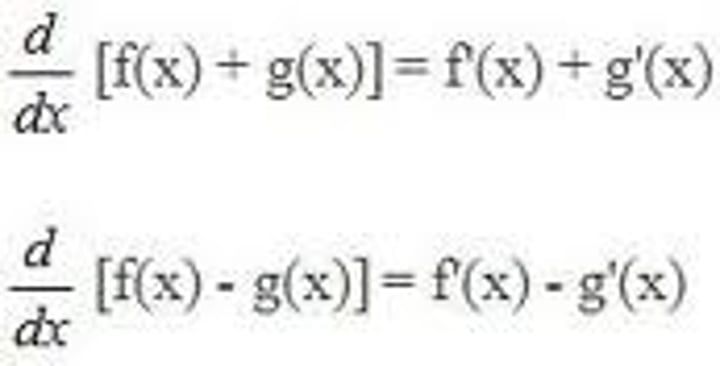
Difference Rule

∫(f - g) dx ∫f dx - ∫g dx

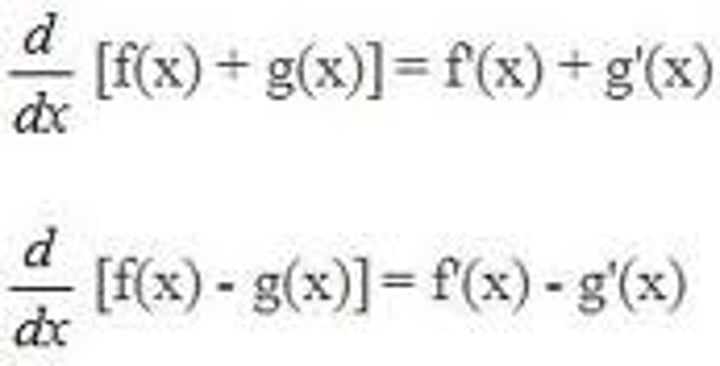
inconsistent linear equations

never intersect

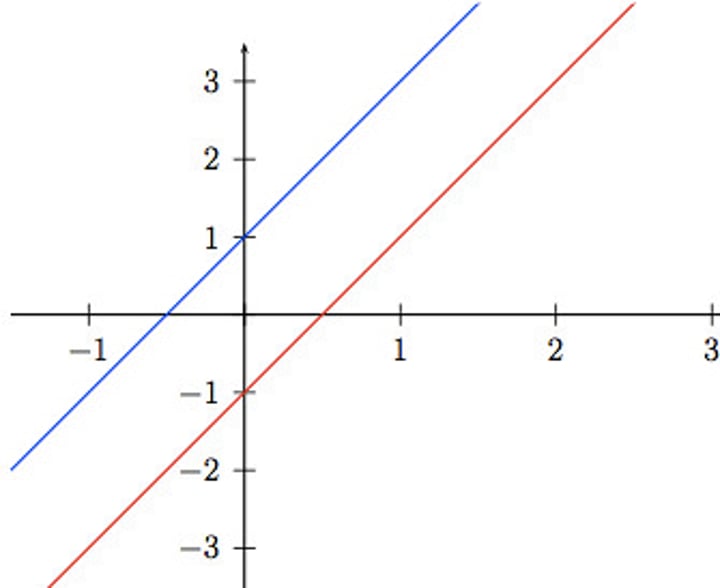
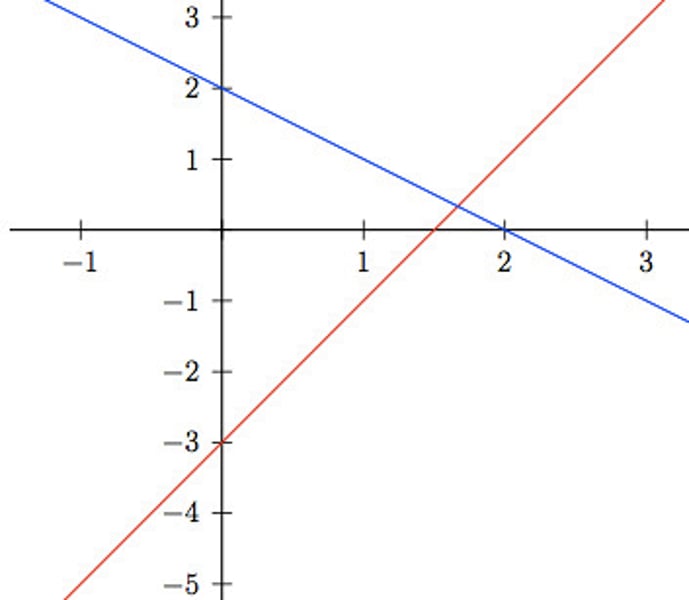
Consistent and independent linear equations

intersect once

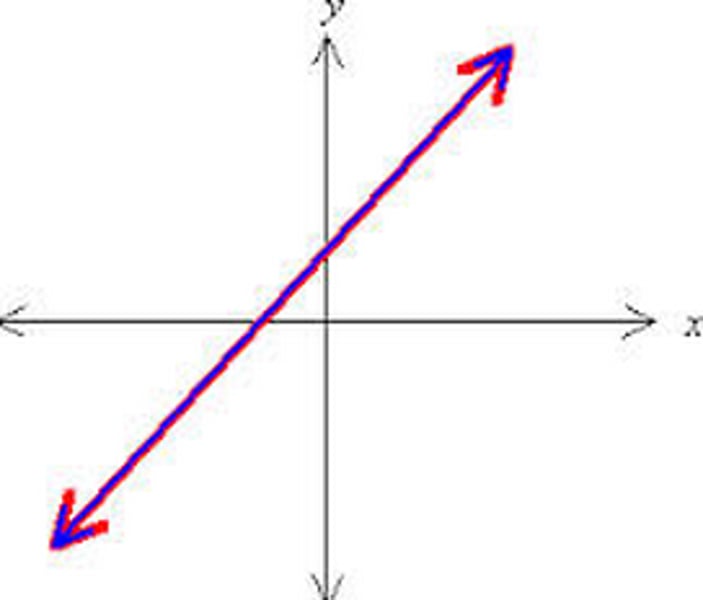
consistent and dependent

same line, infinitely many solutions

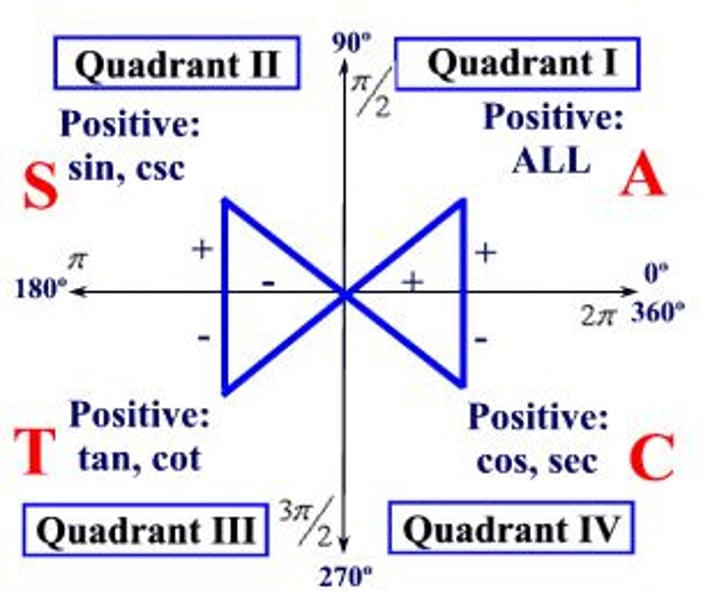
ASTC (All Students Take Calculus)

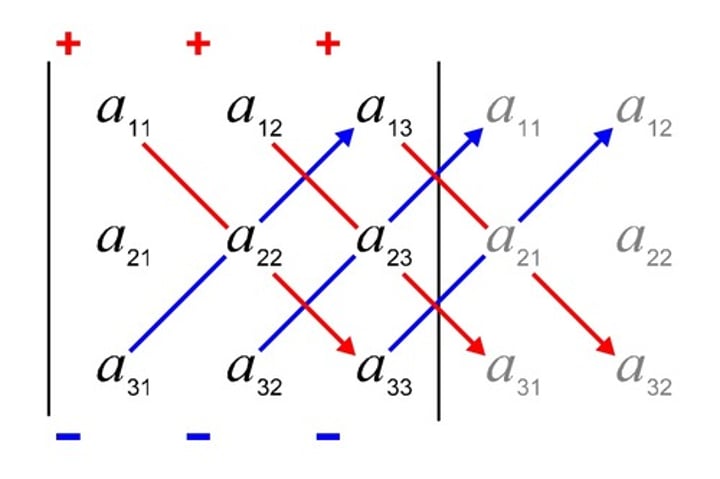
Rule of Sarrus (Used to find determinant of 3*3)

Add product of main diagonals from top to bottom (3), then subtract from the subtraction of products of main diagonals from bottom to top (3)

Transpose of a Matrix

Switch the rows and columns - imagine it kinda swinging up/down a 90-degree angle

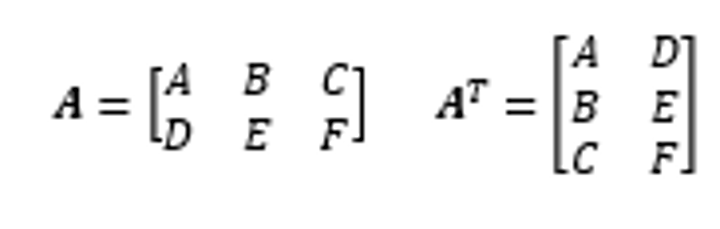
Determinant of Matrix

ad-bc

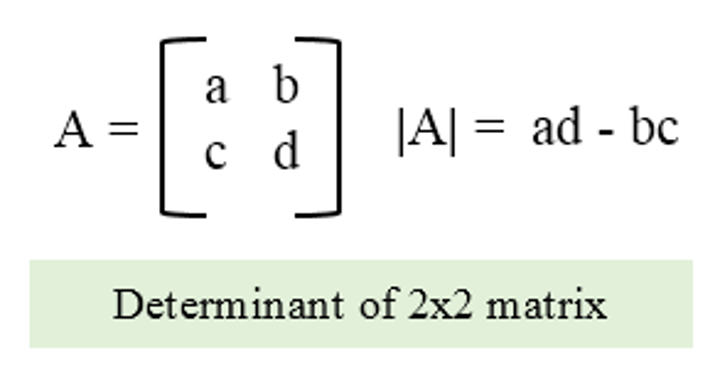
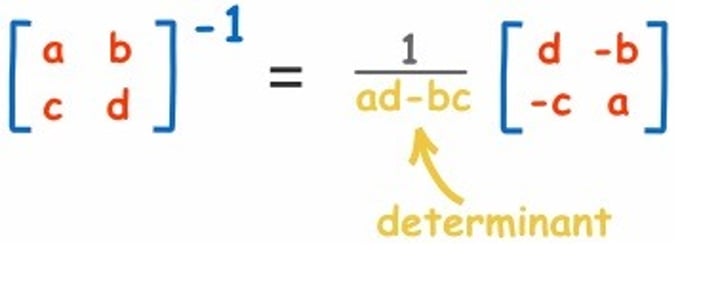
Inverse matrix

two n x n matrices are inverses of each other if their product is the identity matrix

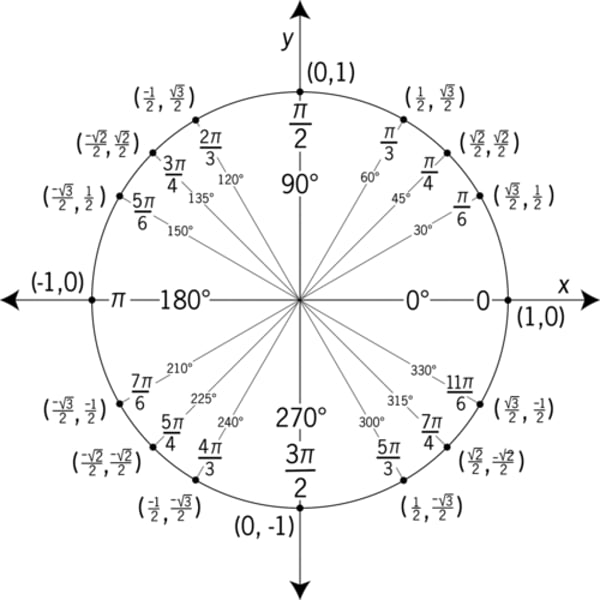
unit circle

a circle with a radius of 1, centered at the origin (cos,sin) To find tan, do sin/cos of that angle

rectangular to polar coordinates

r^2 = x^2 + y^2

tan(θ) = y/x

If not in quadrant I, add 180 for each new quadrant

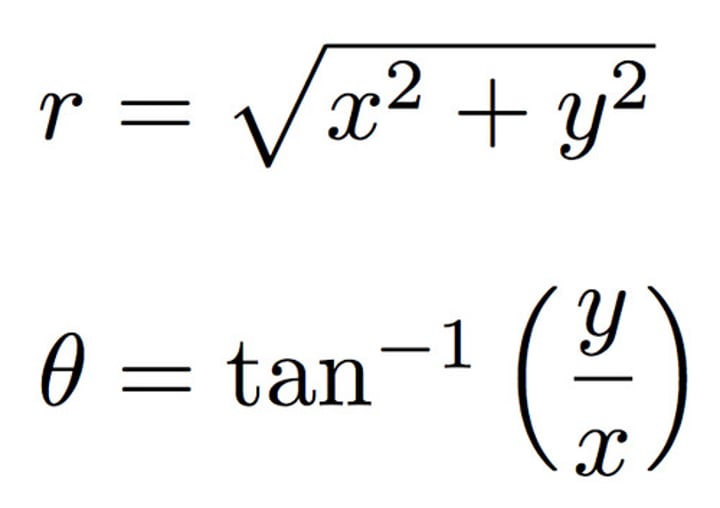
polar to rectangular

x=rcos(theta)

y=rsin(theta)

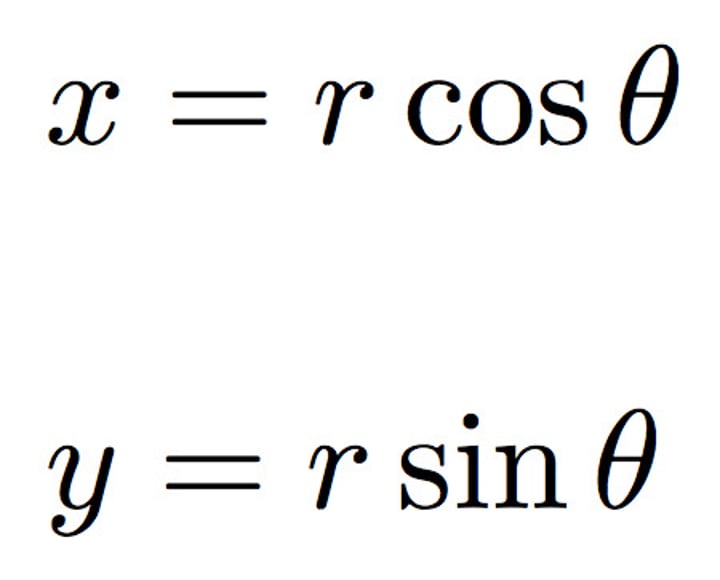
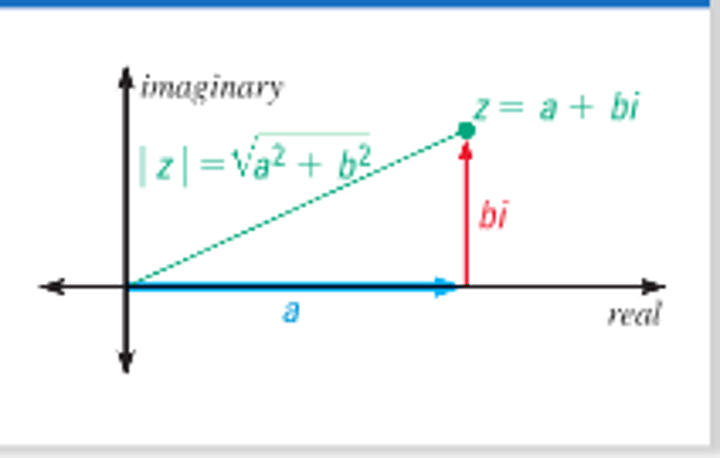
absolute value of a complex number

√a^2+b^2

Argument of a complex number

Measured anticlockwise from the first quadrant. "The angle relateable to polar scale.

Modulus of a complex number

magnitude of the vector

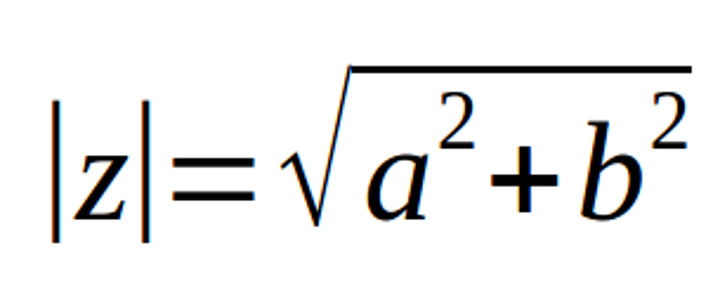
Change of base rule for logs

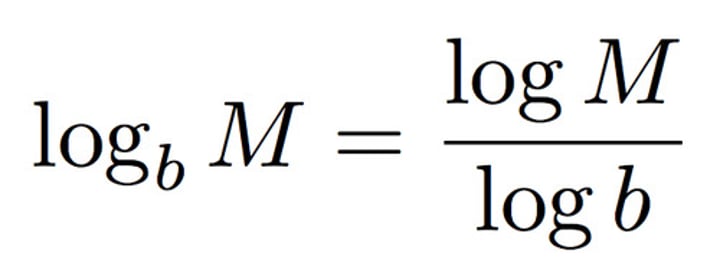
logarithms :power rule

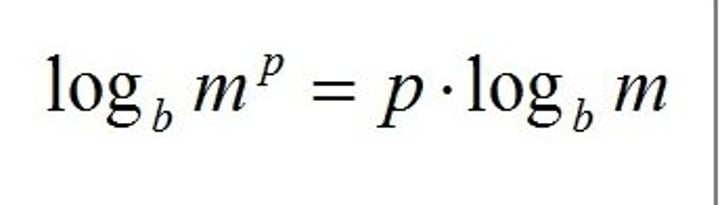
Quotient rule of logarithms

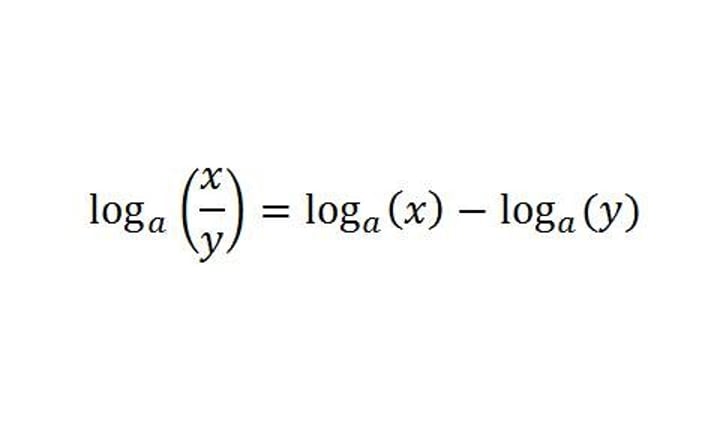
Rational roots theorem

If P(x) is a polynomial with integer coefficients and if is a zero of P(x) ( P( ) = 0 ), then p is a factor of the constant term of P(x) and q is a factor of the leading coefficient of P(x) .

Intersection points of parabola and a circle

Set the two equations equal to each other and solve for y

Standard equation of parabola to find foci

(x−h)2=4p(y−k)(5.2.1)(5.2.1)(x−h)2=4p(y−k)

A parabola is defined as the locus (or collection) of points equidistant from a given point (the focus) and a given line (the directrix). Another important point is the vertex or turning point of the parabola. If the equation of a parabola is given in standard form then the vertex will be(h,k).(h,k).The focus will be a distance ofppunits from the vertex within the curve of the parabola and the directrix will be a distance ofppunits from the vertex outside the curve of the parabola. This value(p)(p)is called the focal distance.

To evaluate limits as x approaches c

Plug in value, use factoring and plug in values, or use conjugates for radicals and plug in

L'Hôpital's Rule

lim f(x)/g(x) = lim f'(x)/g'(x)

Use before plugging in limit

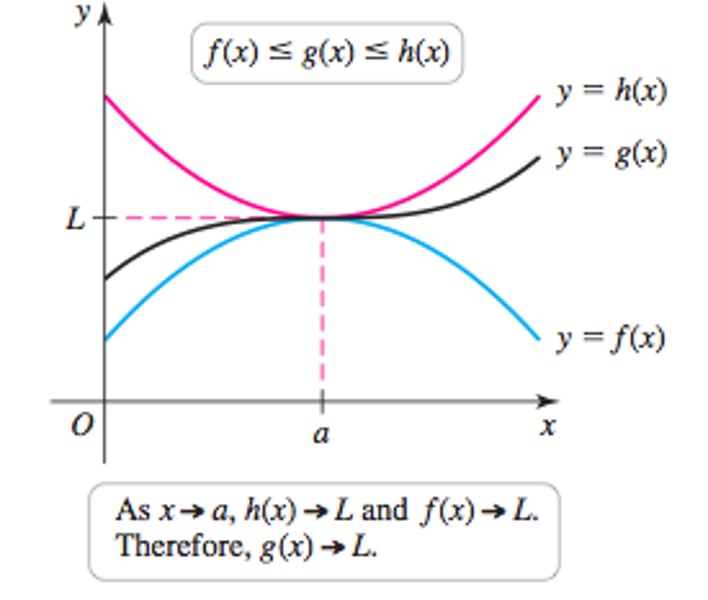
Squeeze Theorem

If f(x) ≤ g(x) ≤ h(x) for all x ̸= a and limx→a f(x) = limx→a h(x) = L, then

limx→a g(x) = L

as x approaches infinity

Then look at the highest degree and determine if - or + infinity

Rules for x approaching infinity

For function: P(x)/Q(x)

If the Degree of P is greater than the Degree of Q ...

... then the limit is positive infinity ...

... or maybe negative infinity. We need to look at the signs!

If the Degree of P is less than the Degree of Q ...

... the limit is 0.

If the Degree of P and Q are the same ...

... divide the coefficients of the terms with the largest exponentcf

Discontinuity of a function

Factor, then find which zero in the denominator cancels out, that is your hole/discontinuity

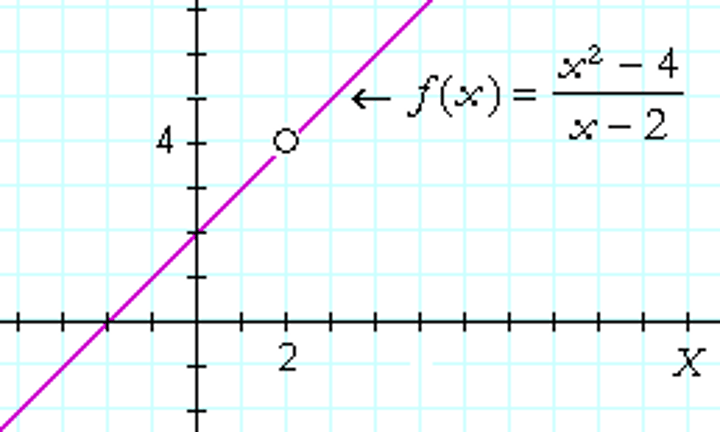
to find y-coordinate of hole

Cancel out repeated factors, then sub in x-value

Asymptote of a graph

the "y-intercept"

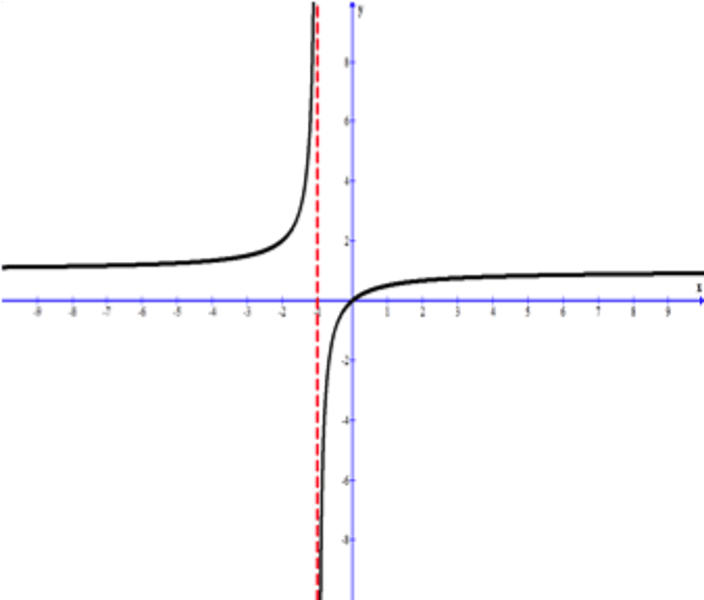
How to find vertical asymptote

1. Set the denominator equal to zero

2. Simplify the fraction

3. Cancel out like terms on the top and the bottom

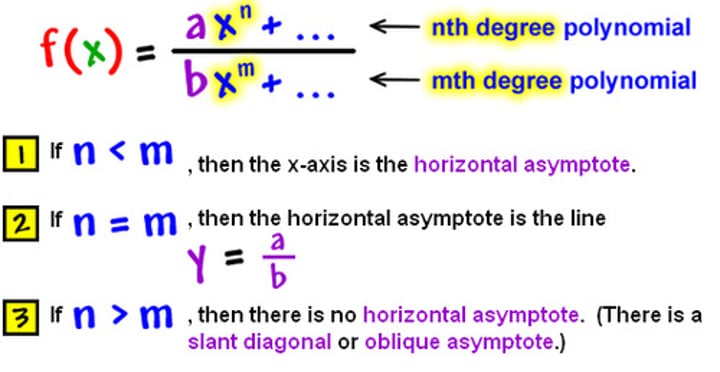
How to find horizontal asymptote

- degree of numerator smaller than degree of denominator - y=0

- degree of numerator same as degree of denominator - y= leading coefficient of numerator/ leading coefficient of denominator

-degree of numerator greater than degree of denominator - no horizontal asymptote

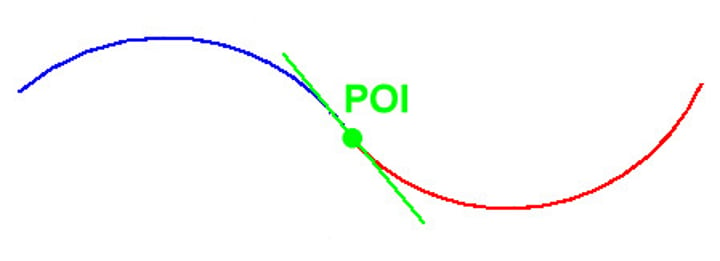
inflection point

A point at which a structure changes curvature from convex to concave. Find by finding second derivative and setting to zero. To find y-value, plug in this second derivative answer into original equation

point of symmetry

the common point of reflection for all points of a figure

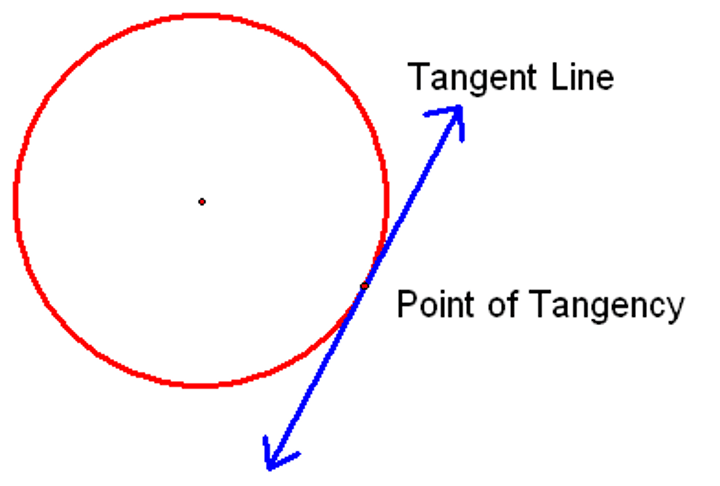
point of tangency

the point where the tangent and a function intersect. You find by getting in slope-intercept form, then find derivative and then substitute in X value to find slope of tangent line.

directrix

a fixed line that is equidistant from the vertex as the focus is to the vertex

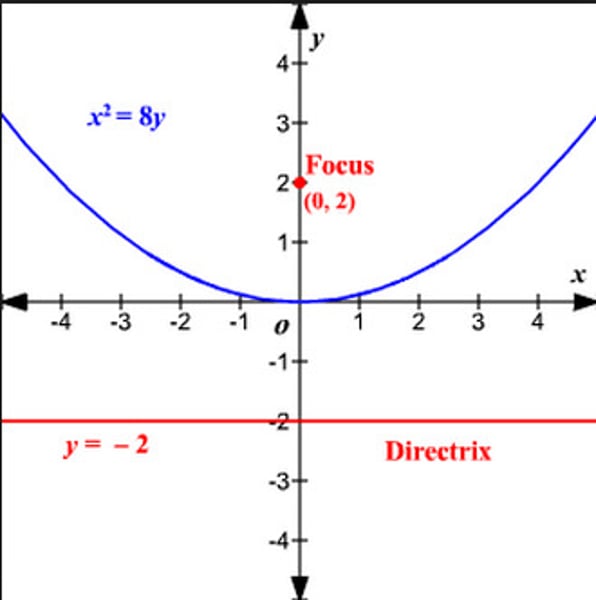
how to find directrix

y=k-p or just get your distance to center or leading coefficient and divide by 4 to get directrix.

Directrix of horizontal parabola

x=h-1/4a

Rotation rules

counterclockwise

90 degrees (x,y)--> (-y,x)

180 degrees (x,y)-->(-x,-y)

270 degrees (x,y) --> (y,-x)

Reflection across y=x

(x,y) -> (y,x)

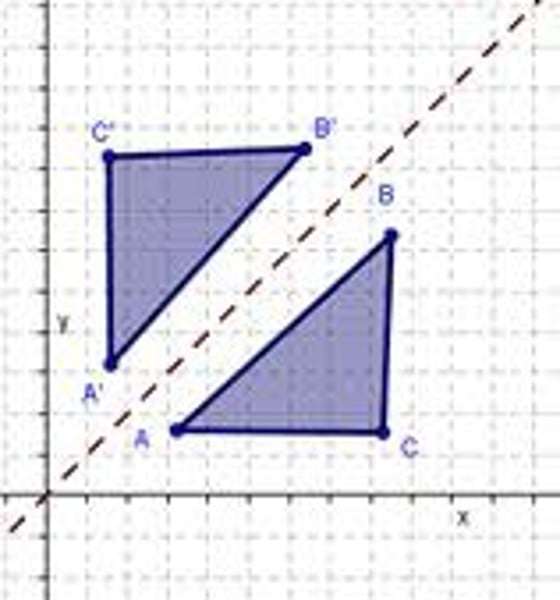
Reflection across y=-x

(x,y) = (-y,x)

Disc method formula

Washer method formula