Kinetic Molecular Theory

F

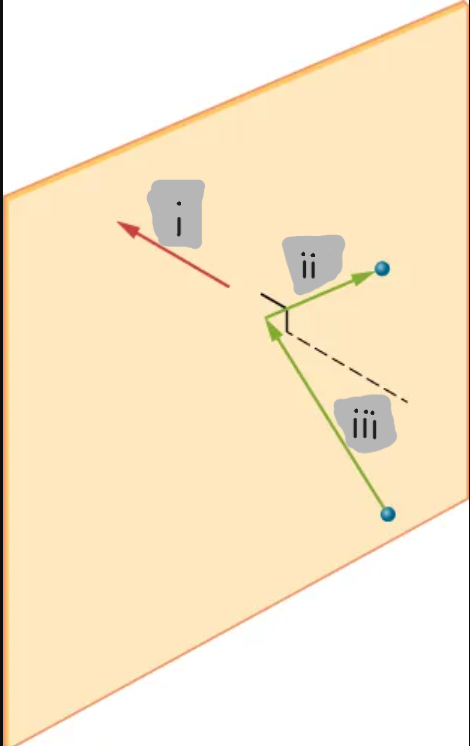
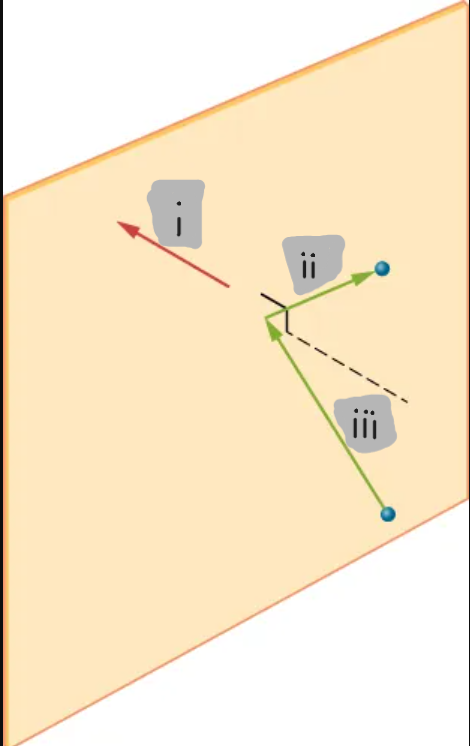
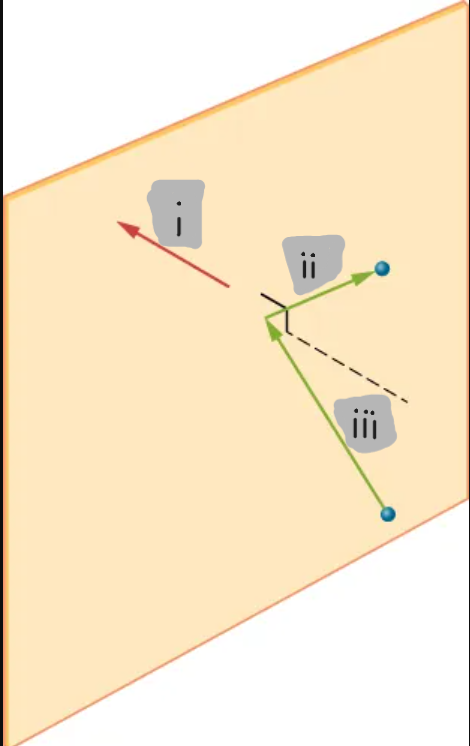
(i)

v’

(ii)

v

(iii)

l

(1)

v’x

(2)

v’y

(3)

vy

(4)

vx

(5)

Kinetic Theory of Gases

A theory that relates macroscopic properties of gases (pressure, temperature, volume) to the microscopic motion of their molecules

A very large number N of identical molecules, each of mass m. Molecules obey Newton’s laws and move randomly and isotropically (equally in all directions)

Microscopic Assumption for an Ideal Gas

Molecules are much smaller than the distance between them (total molecular volume < container volume). Collisions with walls and each other are perfectly elastic. No significant intermolecular forces (attractions, gravity), therefore Isotropic motion.

Assumptions for an ideal gas inside a container.

Monoatomic Ideal Gas

• A gas whole molecules are single atoms

• Example: Helium Gas

• Assumed to have only translational kinetic energy and

• no rotational or vibrational energy

molecular collisions, container walls, collisions, momentum, force, wall

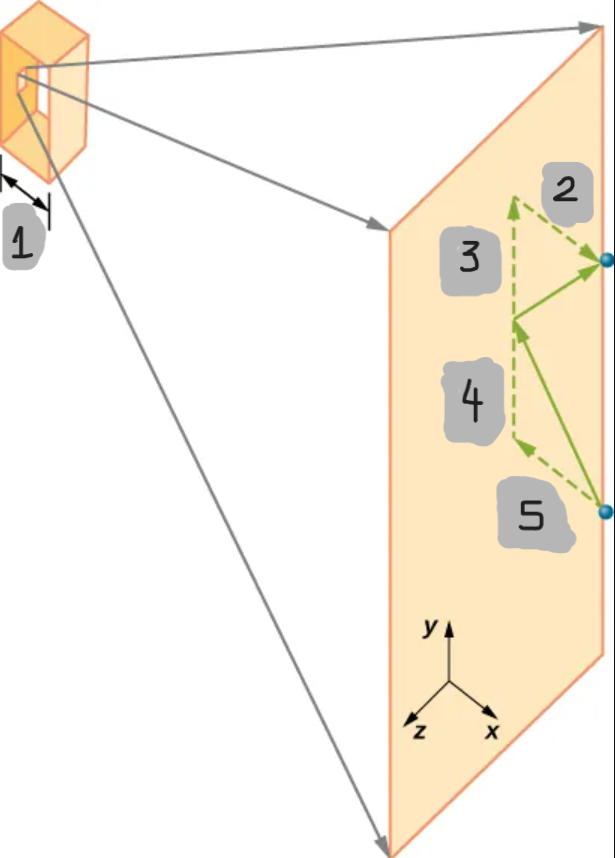
Gas pressure is caused by ____________________ with _______________. Each _________ changes the molecule’s ________ and exerts a _____ on the ____.

-m(v_x)

Initial momentum for one molecule hitting a wall perpendicular to the x-axis

+m(v_x)

Final momentum for one molecule hitting a wall perpendicular to the x-axis

Δp_x = +m(v_x) - (-m(v_x)) = 2m(v_x)

Momentum Change in wall collision for one molecule hitting a wall perpendicular to the x-axis

2l

Round trip distance for the molecule that travels back and forth across the box of length l

v_x

Speed of the molecule for it to travel back and forth across the box of length l

Δt = (2l)/(v_x)

Molecule’s average time between collisions with that wall

F_i = Δp/Δt = (2m(v_x))/((2l)/(v_x)) = (m(v_x)^2)/l

Average force from one molecule on wall

F = ΣF_i = (m/l)Σ(v_ix)^2 = N(m(v̅_x)^2)/l

Total Force on walls from all molecules

v̅^2 = (v̅_x)^2 + (v̅_y)^2 + (v̅_z)^2 = 3((v̅_x)^2); Therefore, (v̅_x)^2 = (v̅^2)/3

For Isotropic Motion, the three directions are equivalent, provide the relationship between v̅² and (v̅_x)²

V = A × l

Volume formula

p = F/A = (Nmv̅^2)/(3V)

Pressure from Molecular Motion

p/V = (1/3)((Nmv̅^2)/(V^2))

key microscopic link to pressure

p = (Nmv̅^2)/(3V)

key microscopic link to pressure (Simplified)

pV = (Nmv̅^2)/3

Linking Kinetic Theory to Ideal Gas Law (Step 1)

pV = N(k_B)T

Linking Kinetic Theory to Ideal Gas Law (Step 2)

((1/3)(mv̅^2)) = ((k_B)T)

Linking Kinetic Theory to Ideal Gas Law (Step 3)

temperature

Average Translational Kinetic Energy per Molecule depends only on the ___________ and not on the type of molecule or pressure

K̅ = ((1/2)(mv̅^2)) = ((3/2)((k_B)T))

Average Translational Kinetic Energy per Molecule

E_int = NK̅ = ((3/2)(N(k_B)T))

Internal Energy of a Monoatomic Ideal Gas (Molecular Form)

N = n(N_A)

N = ?

R = ((N_A)(k_B))

R = ?

E_int = ((3/2)(nRT))

Internal Energy of a Monoatomic Ideal Gas (Mole Form)

Root-mean-squared (rms) Speed

The square root of the average of the square of molecular speed.

v_rms = (v̅^2)^1/2

Mathematical representation of the Root-mean-squared (rms) Speed

v_rms = ((3(k_B)T)/m)^1/2

Root-mean-squared (rms) Speed in Microscopic form

kg/mol

SI unit of Molar Mass

v_rms = ((3RT)/M)^1/2

Root-mean-squared (rms) Speed in Molar form

Yes, it is true

Is it true that at the same temperature, lighter molecules (smaller m or M) have higher rms speeds; heavier molecules move more slowly on average.

helium

A small fraction of molecules in the high-speed tail of the distribution exceed the escape velocity, allowing light gases like ______ to escape from Earth or the Moon over long times.

Atmosphere Loss on the Moon

The Moon’s low gravity → small escape velocity → gas molecules escape easily → almost no atmosphere and black sky even in daytime.

Partial Pressure

The pressure of a gas would exert if it alone occupied the entire volume of the mixture

Dalton’s Law of Partial Pressure

For a mixture of ideal gases total pressure equals the sum of partial pressures of all component gases

p1/n1 = p2/n2 = (RT)/V

Relationship between the Partial Pressure and Moles at the same temperature. (Partial Pressure is directly proportional to the number of moles of that gas)

Vapor Pressure

The equilibrium partial pressure of a vapor in contact with its liquid (or solid) at a given temperature.

Dew Point

The temperature at which air becomes saturated with water vapor and condensation begins (partial pressure of water reaches vapor pressure)

RH = ((Partial pressure of water vapor at T)/(Vapor Pressure of Water at T)) × 100%

Relative Humidity

RH = 100%

Means the air is saturated with water vapor