Proof #3: Two Lines Whose Slopes Are Opposite Reciprocals Are Perpendicular (Proof by Construction and Similar Triangles)

proof goal

Prove that two lines whose slopes are opposite reciprocals are perpendicular

given

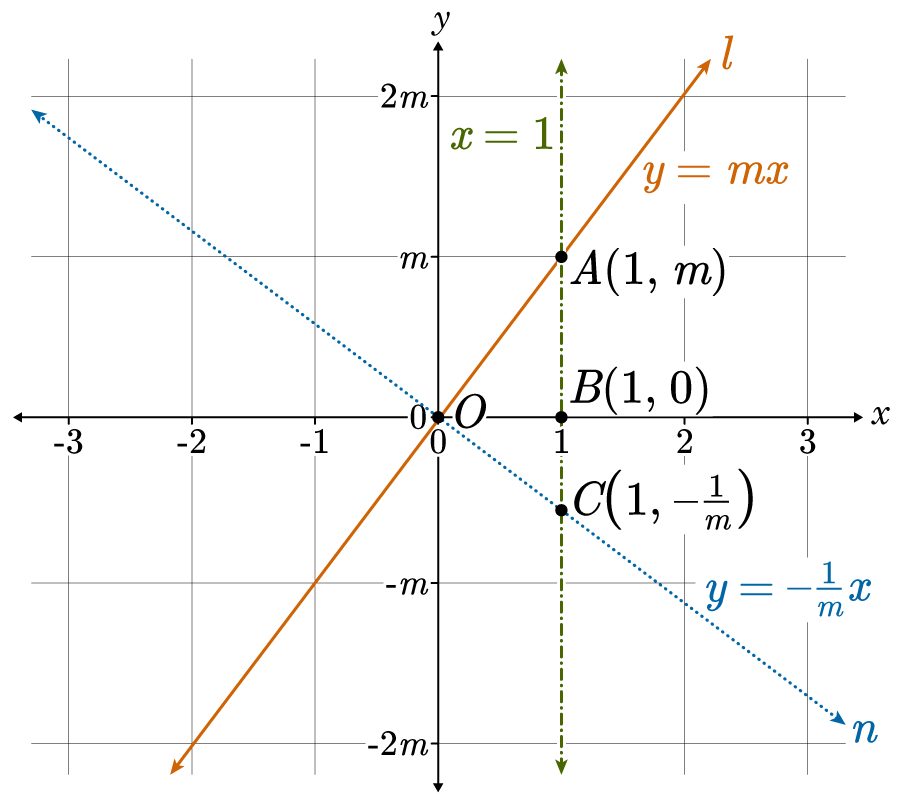
Let line l have slope m and line n have slope −1/m

nonzero condition

m ≠ 0 (so that −1/m is defined)

point of intersection

Let the lines intersect at the origin O(0, 0)

line l equation

y

line n equation

y

construction step

Draw a vertical line at x

point of intersection with l

line l intersects the vertical line at point A(1, m)

point of intersection with n

line n intersects the vertical line at point C(1, −1/m)

triangle formation

Triangles OAB and OBC are formed between the lines and the vertical x

goal restated

Prove that ∠AOC

distance formula

d

calculate OA

√(1² + m²)

calculate OB

1 (horizontal distance)

calculate BA

m (vertical rise from O to A)

calculate OC

√(1 + (1/m)²)

calculate BC

1/m (vertical distance from O to C)

form ratio for triangle OBA

(OB/BA)

form ratio for triangle CBO

(BC/OB)

ratio comparison

The corresponding side ratios are equal

triangle similarity

Therefore, ΔOBA ∼ ΔCBO by SSS similarity

angle correspondence 1

∠OBA ≅ ∠CBO

angle correspondence 2

∠OAB ≅ ∠COB

angle correspondence 3

∠BOA ≅ ∠BCO

triangle sum equation

m∠OBA + m∠OAB + m∠BOA

substitute right angle

90° + m∠OAB + m∠BOA

simplify to get

m∠OAB + m∠BOA

combine equal angles

m∠AOC

logical conclusion

∠AOC is a right angle

final conclusion

Lines l and n, with slopes m and −1/m, are perpendicular

slope product rule

The product of slopes of perpendicular lines equals −1