10: AP Calculus Reference_BC_Differential Equations & Integration Techniques

Differential Equations

Euler’s Method

When to use: Approximate solutions to differential equations when an exact solution is hard to find.

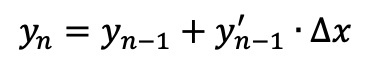
Logistic Differential Equation and Population Growth

Logistic Differential Equations

• P(t): Population at time t.

• k: Growth rate constant.

• L: Carrying capacity (maximum sustainable population).

When to use: Modeling population growth with a carrying capacity L.

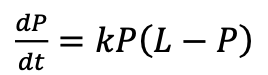
Logistic Differential Equation and Population Growth

Solution to the Logistic Equation

• C: Constant determined by initial conditions.

• The solution describes an S-shaped (sigmoid) growth curve.

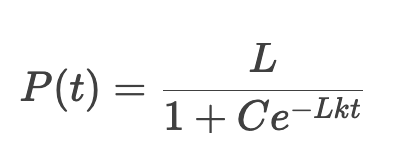
Logistic Differential Equation and Population Growth

Long-Term Behavior

As time approaches infinity, the population approaches the carrying capacity L.

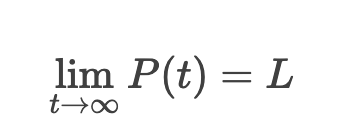
Logistic Differential Equation and Population Growth

Point of Inflection

This is where the growth rate transitions from increasing to decreasing.

Integration Techniques

Integration by Parts

When to use: Integrand is a product of two functions

(e.g., x sin⁡x).

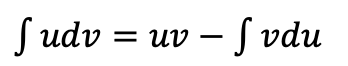
Integration Techniques

Integrating Using Linear Partial Fractions

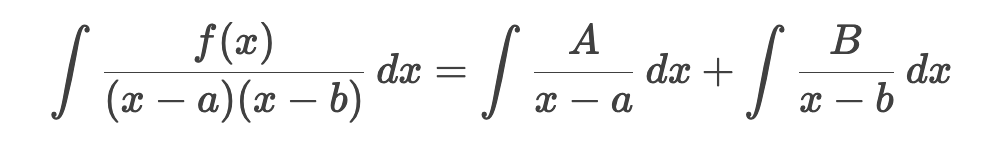
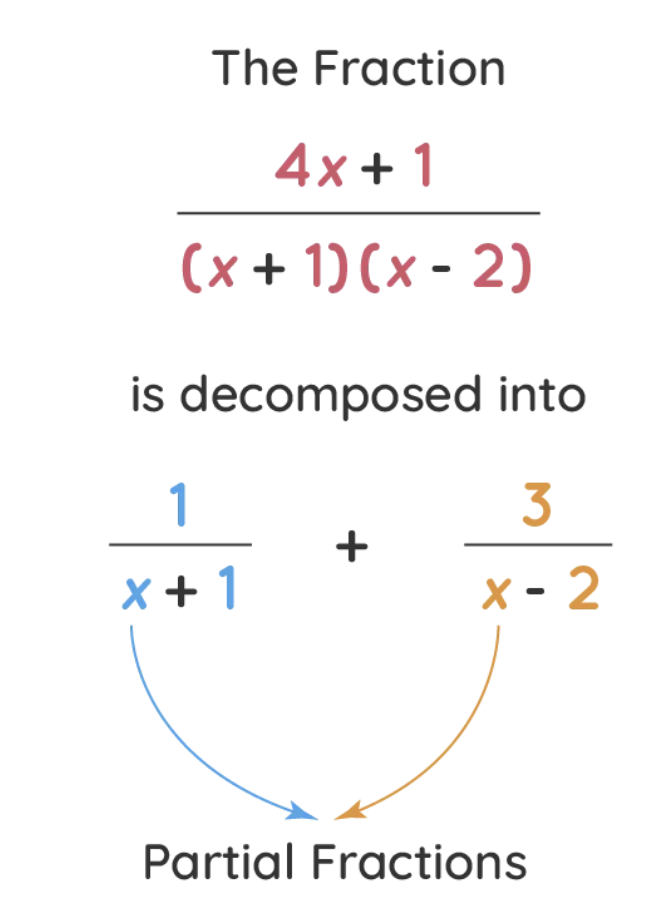
Steps for Partial Fraction Integration

Improper Integrals

An improper integral occurs when the limits of integration involve infinity or when the function being integrated becomes unbounded within the integration interval.

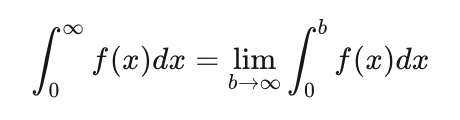
Evaluating Improper Integrals

Population Density Along a Straight Line

Population Density in a Circular Area

Accumulation Formula

Applications of Accumulation Formula

Parametric Equations

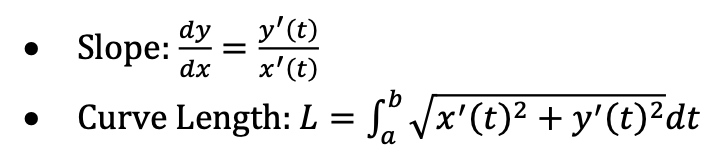
Polar Equations

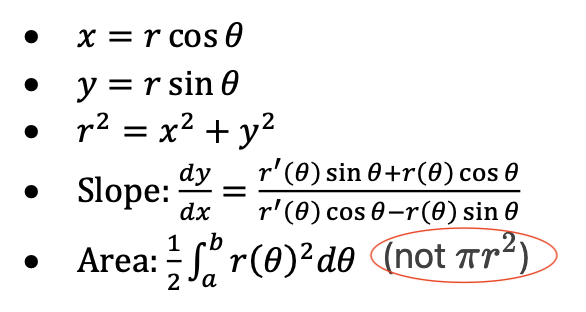
Parametric vs. Polar

• Parametric uses t; Polar uses θ.

• Both require derivatives/integrals for slopes, lengths, and areas.

Vector Calculus

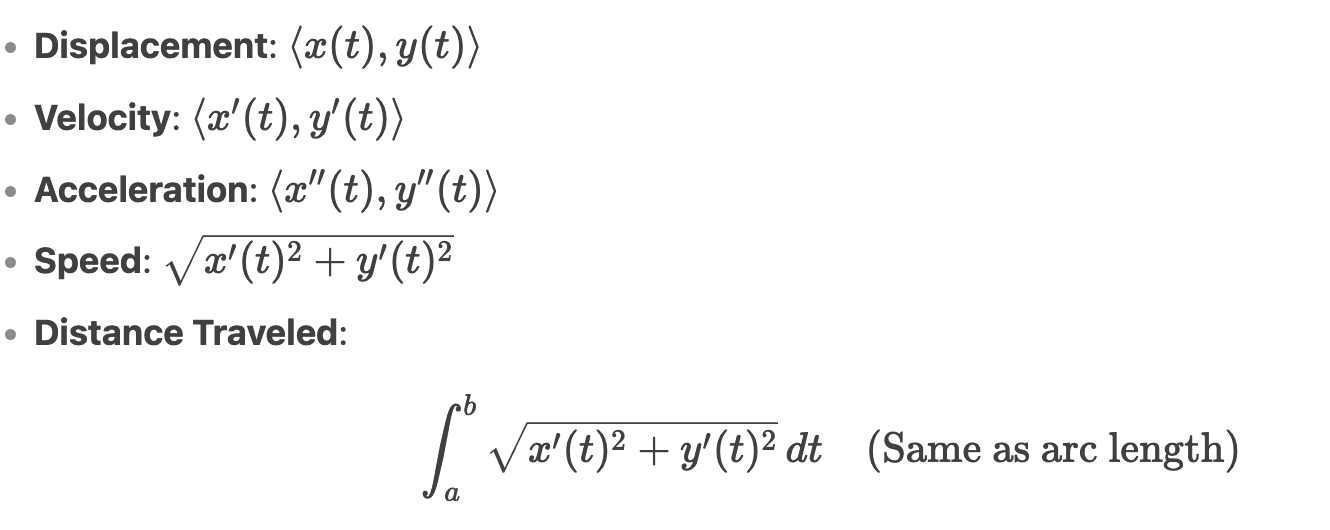
Vector Motion:

• Speed is the magnitude of velocity.

• Distance is the integral of speed.