Trigonometry

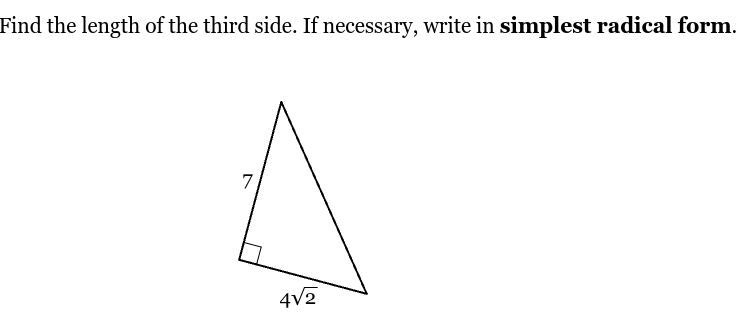
Note: √2 is not a exponent

hypotenuse = 9

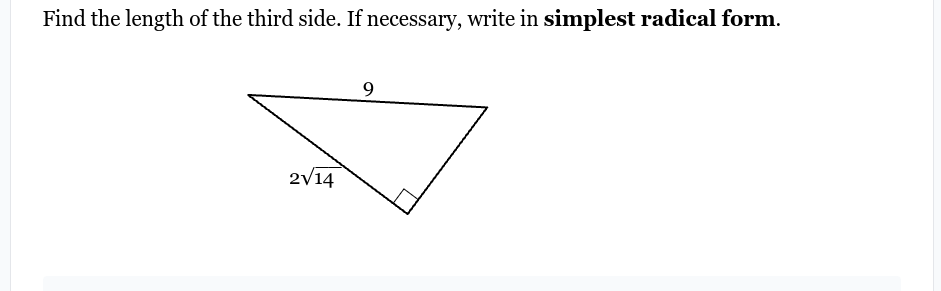
Find the length.

Adjacent = 5

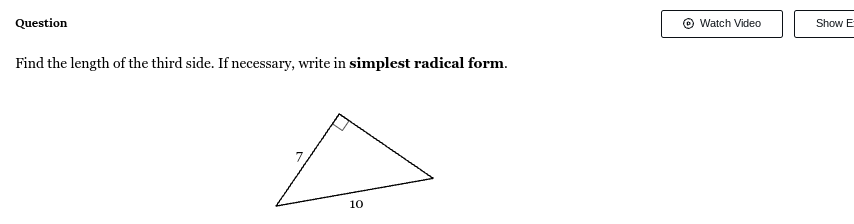
Find the length

Remeber: if the radical does not simplfy to a whole number, write in simplest radical form.

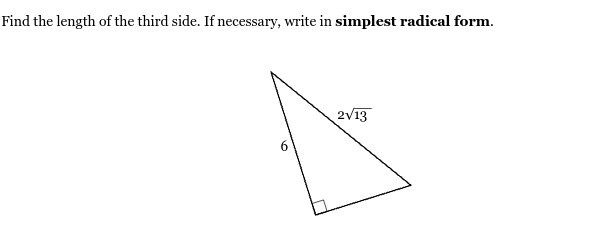
Find length

adjacent = 4

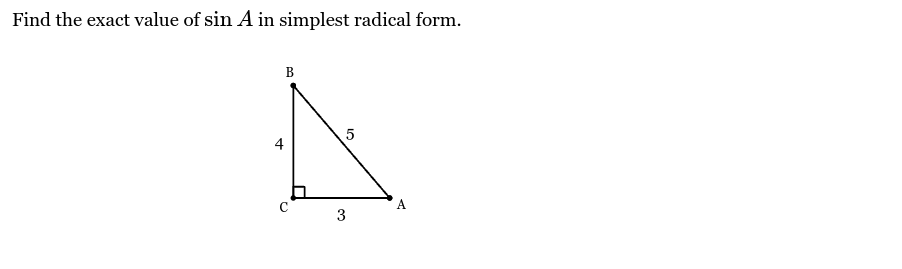
Write equation in simplest form.

Sin(A) = 4/5

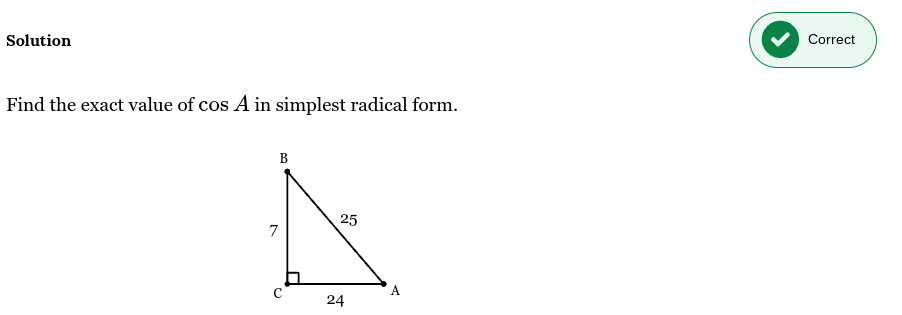
Write equation in simplest form

cos(A) = 24/25

Find the value of tan(A) in simplest radical form.

tan(A) = 2√2

What is the saying that helps you remember how to solve trigonometry?

SOH CAH TOA

What does the SOH stand for in SOH CAH TOA ?

Sin = opp/hyp. (opposite/hypotenuse)

S O H

What does the CAH stand for in SOH CAH TOH ?

Cos = adj/hyp. (adjacent/hypotenuse)

C A H

What does the TOA stand for in SOH CAH TOA ?

Tan = opp/adj (adjacent/hypotenuse

What are trigonometric ratios that relate the angles and sides of a right triangle?

Sin, cos, tan

sin = ?

sin = opp/hyp

cos = ?

cos = adj/hyp

tan = ?

opp/adj

opp is short for..

opposite

adj is short for…

adjacent

hyp is short for…

hypotenuse

What is the pythagorean theorem?

a² + b² = c²

What is the formula for finding the length of one of the sides of a right triangle?

a² + b² = c²

What is the equation for finding the hypotenuse, adjacent, or opposite?

a² + b² = c²

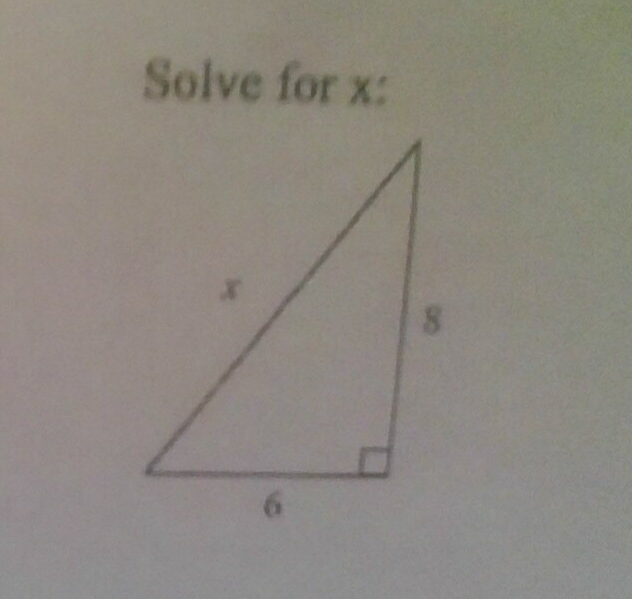
Clarification: x,8,6.

a² + b² = x²

8² + 6² = x²

100 = x²

√100 = √x²

10 = x

What is the a² in a² + b² = c² ?

the adjacent

What is the b² in a² + b² = c² ?

the opposite

What is the c² in a² + b² = c² ?

hypotenuse

The opposite is always…

across from the given angle

When labeling a side, how would you organize/ portray it?

if the line is hypotenuse, most likely ac = ?, if the line is adjacent then bc, etc.

Ex: ab = 10, ac = 12

What is the name of this symbol: θ

the theta. NOT THE SAME AS 0

When graphing a right triangle on a graph with a single point how do you graph the rest of the triangle?

Draw a line form the origin to the dot then another line at the middle to make it a full triangle

Remeber: the ____ of a the triangle can never be ____

length, negative

The length of a triangle is always a ______ number.

positive

When graphing the right triangle, the angle is always located at….

at the origin

The adjacent is usually the _____ side

shortest/bottom

The hypotenuse is always the ______ side.

longest

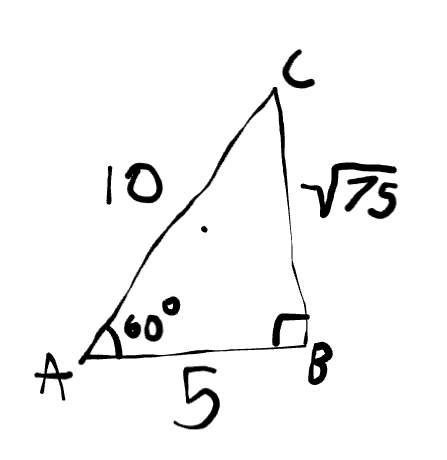
Identify the hypotenuse.

ac = 10

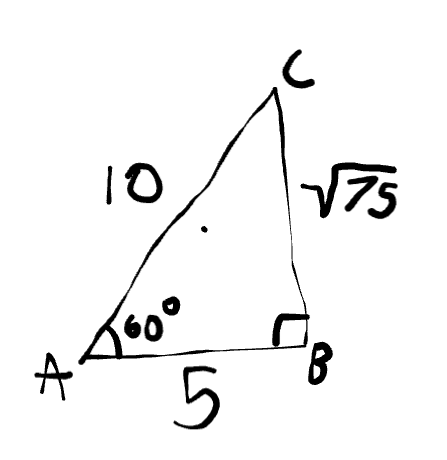
Identify the side that is opposite to 60°

bc = √75

Identify the side that is adjacent to 60°

ab = 5

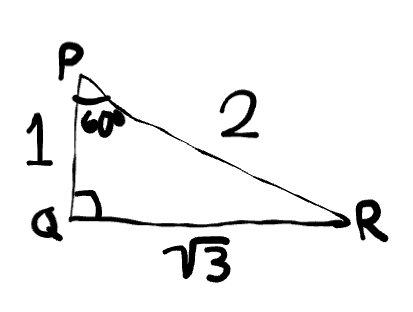
Identify the hypotenuse.

PR = 2

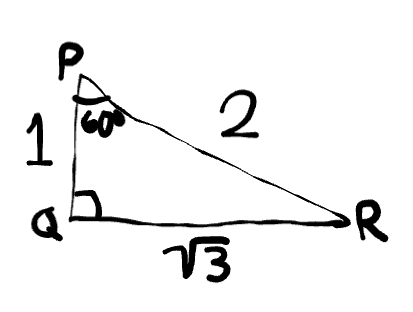
Identify the side that is opposite to 60°

QR = √3

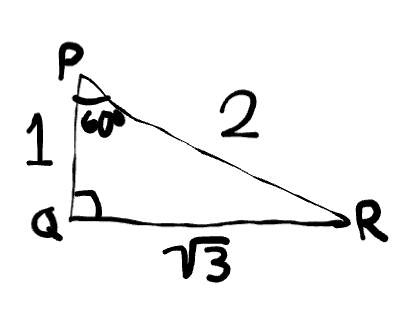
Identify the side that is adjacent to 60°

PQ = 1

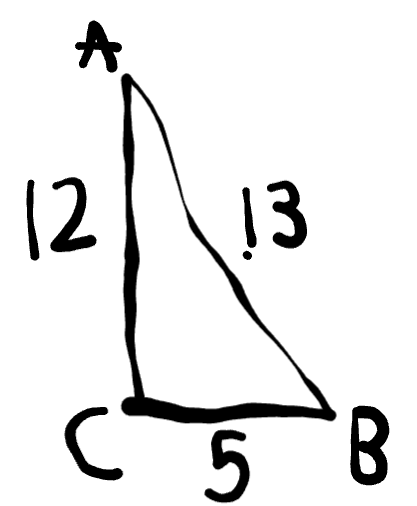
Find Cos(B)

cos(b) = 5/13

If θ is an angle in standard position whose terminal side passes through the point (-2,-3), what is thenumerical value of tanθ ?

Tip: use a graph.

tan(θ) = 3/2

Note: length cannot be negative

csc = ?

csc = hyp/opp

sec = ?

sec = hyp/adj

cot = ?

cot = adj/opp

The opposite of sin is…

csc. sin = opp/hyp then csc = hyp/opp

The opposite of csc is…

sin. sin = opp/hyp then csc = hyp/opp

The opposite of cos is…

sec. cos = adj/hyp then sec = hyp/adj

The opposite of sec is…

cos. cos = adj/hyp then sec = hyp/adj

The opposite of tan is…

cot. tan = opp/adj then cot = adj/opp

The opposite of cot is…

tan. tan = opp/adj then cot = adj/opp

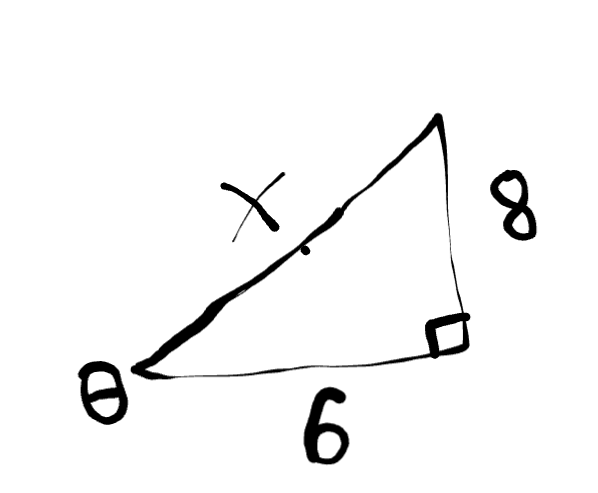
What is the cos of θ?

Cos(θ) = 3/5

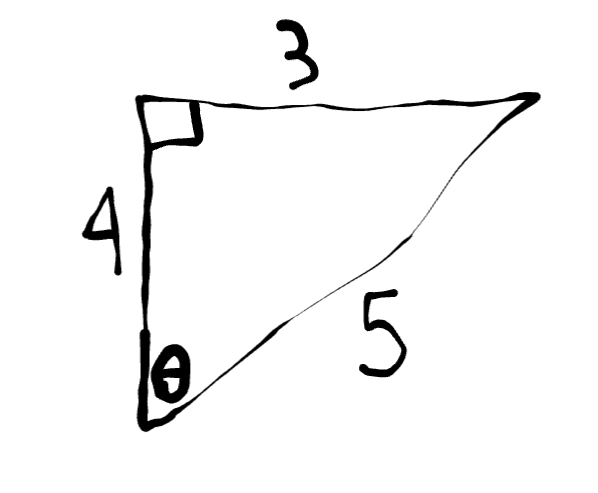
Find the value of: cot θ

cot θ = 3/4.

Remember: con is the opposite of tan.

Determine the exact value of csc(P) if P is an angle in standard position and its terminal side passes through the point (5,-8)

Tip: Use graph paper

csc(P) = √89 / 8

If the terminal side of θ, in standard position, passes through point (-4,3), what is the numerical value of sin θ?

sin(θ) = 3/5

If the terminal side of angle θ passes through point (-3,-4), what is the value of sec θ?

sec θ = 5/3