Kõrgem matemaatika I EKSAM
0.0(0)
0.0(0)
Card Sorting
1/49
Earn XP
Description and Tags
Last updated 6:59 PM on 12/19/22
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
50 Terms
1
New cards
Ratsionaalarvud
Ratsionaalarvudeks nimetatakse arve x, mis on esitatavad kujul
x = p/q , kus p ∈ Z ja q ∈ N. Kõigi ratsionaalarvude hulga tähistame sümboliga Q.
x = p/q , kus p ∈ Z ja q ∈ N. Kõigi ratsionaalarvude hulga tähistame sümboliga Q.
2
New cards
Irratsionaalarvud
Arve, mis on esitatavad lõpmatute mitteperioodiliste kümnendmurdudena, nimetatakse irratsionaalarvudeks. Tähistatakse sümboliga I.
3
New cards
Reaalarvu absoluutväärtus
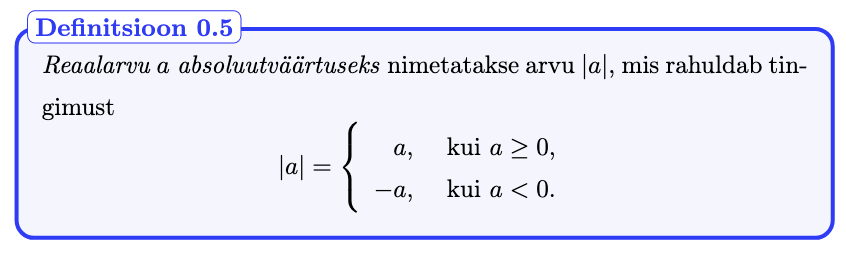
4
New cards
Absoluutväärtuse tähtsamad omadused

5
New cards
Newtoni binoomvalem

6
New cards
Ülalt tõkestatud hulk
Olgu X ⊂ R. Öeldakse, et hulk X on ülalt tõkestatud, kui leidub arv M ∈ R selliselt, et x ≤ M iga x ∈ X korral; arvu M nimetatakse sel juhul hulga X ülemiseks tõkkeks
7
New cards
Alt tõkestatud hulk
Olgu X ⊂ R. Öeldakse, et hulk X on alt tõkestatud, kui leidub arv m ∈ R selliselt, et x ≥ m iga x ∈ X korral; arvu m nimetatakse sel juhul hulga X alumiseks tõkkeks.
8
New cards
Tõkestatud hulk
Olgu X ⊂ R. Öeldakse, et hulk X on tõkestatud, kui ta on nii ülalt kui ka alt tõkestatud, s.t. leiduvad arvud m, M ∈ R selliselt, et m ≤ x ≤ M iga x ∈ X korral.
9
New cards
Piisav ja tarvilik tingimus hulga tõkestatuseks
Hulk X ⊂ R on tõkestatud parajasti siis, kui leidub arv L ∈ R selliselt, et
|x| ≤ L iga x ∈ X korral.
|x| ≤ L iga x ∈ X korral.
10
New cards
Hulga ülemine raja
Olgu hulk X ⊂ R ülalt tõkestatud. Hulga X vähimat ülemist tõket nimetatakse hulga X ülemiseks rajaks ja tähistatakse sümboliga sup X
11
New cards
Hulga alumine raja
Olgu hulk X ⊂ R alt tõkestatud. Hulga X suurimat alumist tõket nimetatakse hulga X alumiseks rajaks ja tähistatakse sümboliga inf X
12
New cards
Pidevuse aksioom
(a) Igal mittetühjal ülalt tõkestatud reaalarvude hulgal on olemas ülemine raja.
(b) Igal mittetühjal alt tõkestatud reaalarvude hulgal on olemas alumine raja.
(b) Igal mittetühjal alt tõkestatud reaalarvude hulgal on olemas alumine raja.
13
New cards
Piisav ja tarvilik tingimus selleks, et arv M oleks hulga ülemiseks rajaks.
Olgu X ⊂ R ning olgu M ∈ R. Arv M on hulga X ülemine raja parajasti siis, kui kehtivad järgmised kaks tingimust:
1◦ x ≤ M iga x ∈ X korral;
2◦ mis tahes reaalarvu ε > 0 korral leidub xε ∈ X selliselt, et xε > M − ε.
1◦ x ≤ M iga x ∈ X korral;
2◦ mis tahes reaalarvu ε > 0 korral leidub xε ∈ X selliselt, et xε > M − ε.
14
New cards
Piisav ja tarvilik tingimus selleks, et arv M oleks hulga alumiseks rajaks
Olgu X ⊂ R ning olgu m ∈ R. Arv m on hulga X alumine raja parajasti siis, kui kehtivad järgmised kaks tingimust:
1◦ x ≥ m iga x ∈ X korral;
2◦ mis tahes reaalarvu ε > 0 korral leidub xε ∈ X selliselt, et xε < m + ε.
1◦ x ≥ m iga x ∈ X korral;
2◦ mis tahes reaalarvu ε > 0 korral leidub xε ∈ X selliselt, et xε < m + ε.
15
New cards
Hulga suurim element
Olgu X ⊂ R. Kui element u ∈ X on selline, et
x ≤ u iga x ∈ X korral, siis elementi u nimetatakse hulga X suurimaks elemendiks ja tähistatakse sümboliga max X
x ≤ u iga x ∈ X korral, siis elementi u nimetatakse hulga X suurimaks elemendiks ja tähistatakse sümboliga max X
16
New cards
Hulga vähim element
Olgu X ⊂ R. Kui element v ∈ X on selline, et
x ≥ v iga x ∈ X korral, siis elementi v nimetatakse hulga X vähimaks elemendiks ja tähistatakse sümboliga min X
x ≥ v iga x ∈ X korral, siis elementi v nimetatakse hulga X vähimaks elemendiks ja tähistatakse sümboliga min X
17
New cards
Suurima ja vähima elemendi ühesus
Mis tahes reaalarvude hulgal saab olla ülimalt üks suurim element ja ülimalt üks vähim element.
18
New cards
Ülemise ja alumise raja ühesus
(a) Ülalt tõkestatud mittetühjal reaalarvude hulgal on täpselt üks ülemine raja.
(b) Alt tõkestatud mittetühjal reaalarvude hulgal on täpselt üks alumine raja.
(b) Alt tõkestatud mittetühjal reaalarvude hulgal on täpselt üks alumine raja.
19
New cards
Hulga suurima elemendi ja ülemise raja vaheline seos
Kui mingis reaalarvude hulgas leidub suurim element, siis see suurim element on selle hulga ülemine raja.
20
New cards
Hulga vähima elemendi ja alumise raja vaheline seos
Kui mingis reaalarvude hulgas leidub vähim element, siis see vähim element on selle hulga alumine raja.
21
New cards
Hulga αX ülemine raja juhul α ⩾ 0
Olgu X ülalt tõkestatud reaalarvude hulga mittetühi alamhulk. Kui α ≥ 0, siis hulk αX on ülalt tõkestatud, kusjuures sup αX = α sup X.
22
New cards
Hulga αX alumine raja juhul α ⩽ 0
Olgu X ülalt tõkestatud reaalarvude hulga mittetühi alamhulk. Kui α ≤ 0, siis hulk αX on alt tõkestatud, kusjuures inf αX = α sup X.
23
New cards
Hulga αX alumine raja juhul α ⩾ 0
Olgu X alt tõkestatud reaalarvude hulga mittetühi alamhulk. Kui α ≥ 0, siis hulk αX on alt tõkestatud, kusjuures inf αX = α inf X
24
New cards
Hulga αX ülemine raja juhul α ⩽ 0
Olgu X alt tõkestatud reaalarvude hulga mittetühi alamhulk. Kui α ≤ 0, siis hulk αX on ülalt tõkestatud, kusjuures sup αX = α inf X
25
New cards
Kahe hulga summa ülemine raja
Olgu X ja Y ülalt tõkestatud reaalarvude hulga mittetühjad alamhulgad, siis hulk X + Y on ülalt tõkestatud, kusjuures sup(X + Y ) = sup X + sup Y
26
New cards
Kahe hulga summa alumine raja
Olgu X ja Y alt tõkestatud reaalarvude hulga mittetühjad alamhulgad, siis hulk X + Y on alt tõkestatud, kusjuures inf(X + Y ) = inf X + inf Y
27
New cards
Kahe hulga vahe ülemine raja
Olgu X ja Y reaalarvude hulga R mittetühjad alamhulgad. Olgu hulk X ülalt tõkestatud ja hulk Y alt tõkestatud. Siis hulk X − Y on ülalt tõkestatud, kusjuures sup(X − Y ) = sup X − inf Y.
28
New cards
Kahe hulga vahe alumine raja
Olgu X ja Y reaalarvude hulga R mittetühjad alamhulgad. Olgu hulk X alt tõkestatud ja hulk Y ülalt tõkestatud. Siis hulk X − Y on alt tõkestatud, kusjuures inf(X − Y ) = inf X − sup Y.
29
New cards
sup X ja inf Y vaheline seos, kui iga x ∈ X, y ∈ Y korral x ⩽ y
Olgu X ja Y reaalarvude hulga R mittetühjad alamhulgad. Kehtigu mis tahes x ∈ X ja y ∈ Y korral võrratus x ≤ y, siis hulk X on ülalt tõkestatud ja hulk Y on alt tõkestatud, kusjuures sup X ≤ inf Y
30
New cards
Arvjada
Kui igale naturaalarvule n on seatud vastavusse kindel reaalarv xn, siis öeldakse, et on antud arvjada (ehk lihtsalt jada)
31
New cards
Ülalt tõkestatud jada
Öeldakse, et arvjada (xn) on ülalt tõkestatud, kui tema liikmete hulk on ülalt tõkestatud, s.t. leidub arv M ∈ R nii, et xn ≤ M iga n ∈ N korral
32
New cards
Alt tõkestatud jada
Öeldakse, et arvjada (xn) on alt tõkestatud, kui tema liikmete hulk on alt tõkestatud, s.t. leidub arv m ∈ R nii, et xn ≥ m iga n ∈ N korral.
33
New cards
Tõkestatud jada
Öeldakse, et arvjada (xn) on tõkestatud, kui tema liikmete hulk on tõkestatud, s.t. leiduvad arvud M, m ∈ R nii, et m ≤ xn ≤ M iga n ∈ N korral.
34
New cards
Jada piirväärtus
Öeldakse, et arv a ∈ R on jada (xn) piirväärtus ja kirjutatakse
lim n→∞ xn = a kui iga reaalarvu ε > 0 korral leidub indeks N ∈ N selliselt, et n ∈ N, n ≥ N =⇒ |xn − a| < ε.
lim n→∞ xn = a kui iga reaalarvu ε > 0 korral leidub indeks N ∈ N selliselt, et n ∈ N, n ≥ N =⇒ |xn − a| < ε.
35
New cards
Arvu ε-ümbrus
Olgu a ∈ R ning olgu ε ∈ R, ε > 0. Vahemikku (a − ε, a + ε) nimetatakse arvu a (või punkti a) ε-ümbruseks
36
New cards
Koonduv jada
Öeldakse, et arvjada (xn) on koonduv, kui tal on olemas piirväärtus a ∈ R. Sel juhul öeldakse ka, et jada (xn) koondub arvuks a.
37
New cards
Hajuv jada
Öeldakse, et arvjada on hajuv, kui ta pole koonduv.
38
New cards
Koonduva jada piirväärtuse ühesus
Koonduva jada piirväärtus on üheselt määratud.
39
New cards
Koonduva jada tõkestatus
Koonduv jada on tõkestatud.
40
New cards
Hääbuv jada
Öeldakse, et arvjada (xn) on hääbuv (ehk lõpmata väike), kui lim xn = 0
41
New cards
Tõkestatud ja hääbuva jada korrutise piirväärtus
Tõkestatud jada ja hääbuva jada korrutis on hääbuv jada.
42
New cards
Koonduvate jadade omadused, mis on seotud aritmeetiliste tehetega

43
New cards
Jada piirväärtuse monotoonsus

44
New cards
Jada (xn) piirväärtus juhul kui mingist indeksist xn ⩽ b (xn ⩾ b)

45
New cards
Jada piirväärtuse sändvitš-teoreem

46
New cards
Jadade ( n√a) (a > 0) ja ( n√n) piirväärtus
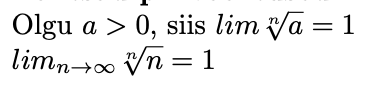
47
New cards
Jada (an) piirväärtus
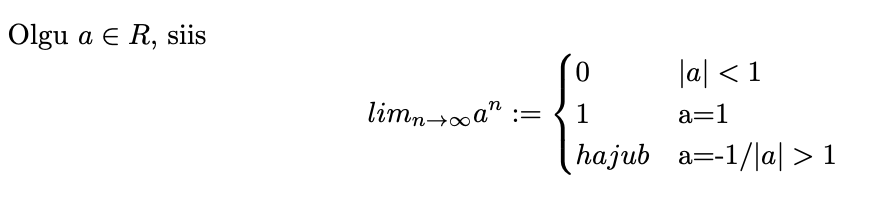
48
New cards
Jada
((1 + 1/n) astmes n) piirväärtus
((1 + 1/n) astmes n) piirväärtus
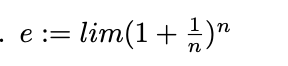
49
New cards
Hulga kuhjumispunkt

50
New cards
Funktsiooni piirväärtus lim f(x) = A, kus a, A € R U (-inf, +inf)