CLEP EXAM - PRECALCULUS

natural numbers

1, 2, 3, 4, and so on.

exponential growth model

A(t)=A(o)e^rt

whole numbers

0, 1, 2, 3, and so on.

integers

0, ±1, ±2, ±3, and so on.

perfect squares

1 4 9 16 25 36 49 64, and so on.

rational number

A rational number is simply a number of arithmetic: Any whole number, fraction, mixed number, or decimal; together with its negative image.

A rational number can always be written in what form?

As a fraction, where a and b are integers (b not equal to 0).

Which natural numbers have rational square roots?

Only the square roots of the square numbers; that is, the square roots of the perfect squares.

real number

A real number is distinguished from an imaginary or complex number. It is what we call any rational or irrational number.

They are the numbers we expect to find on the number line.

They are the numbers we need for measuring.

function

A rule that relates two variables, typically x and y

domain

The values that x may assume

range

the values of y that correspond to the values of x

value of the function

value of y

independent variable

x

dependent variable

y

f(x) = x2 and g(x) = x + h.

f(g(x))

f(x + h) = (x + h)2 = x2 + 2xh + h2

f(x) = x2 and g(x) = x + h.

g(f(x))

g(x2) = x2 + h

Let f(x) = x5 and g(x) = x1/5

f(g(x))

x

Let f(x) = x5 and g(x) = x1/5

g(f(x))

x

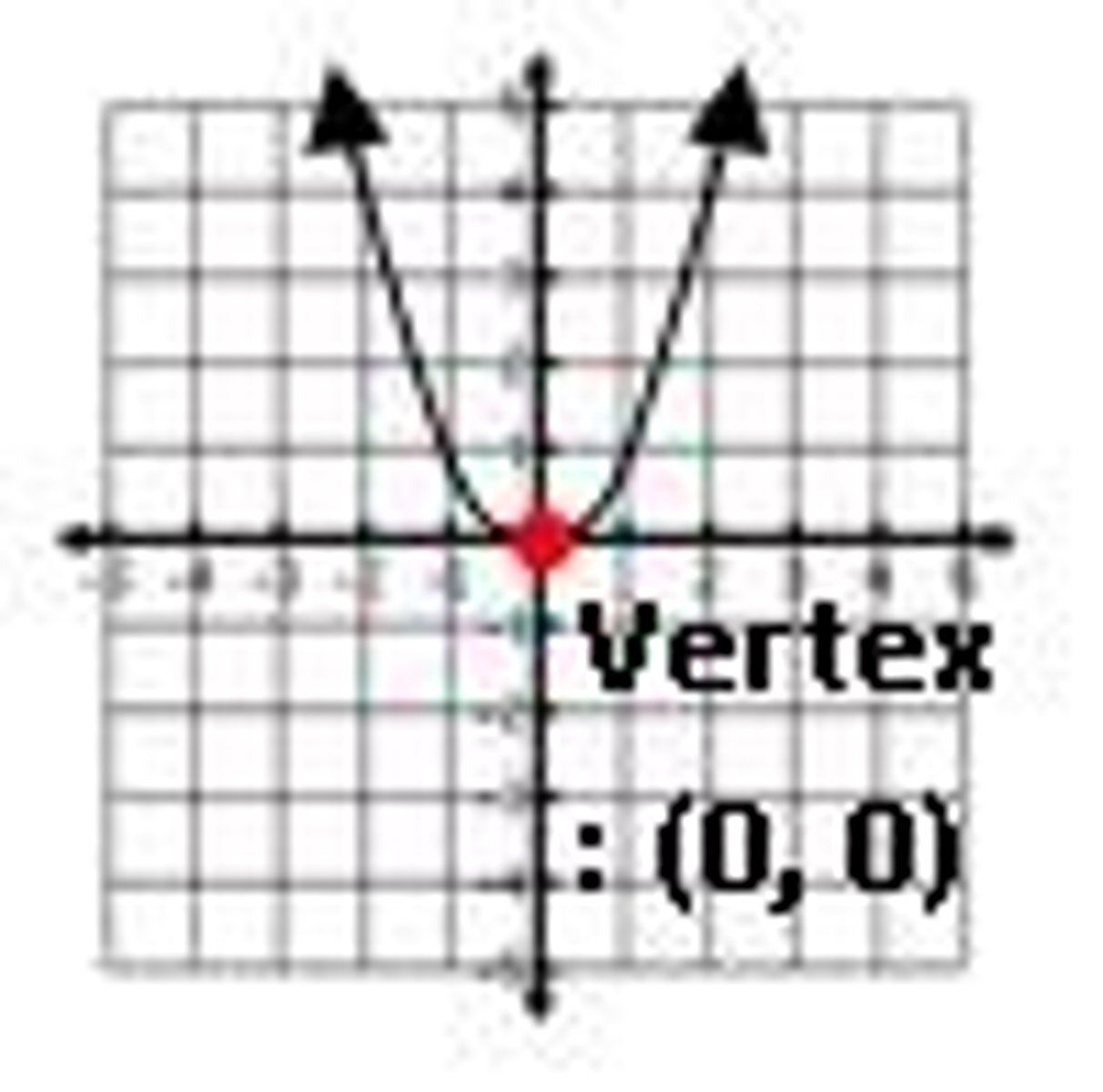
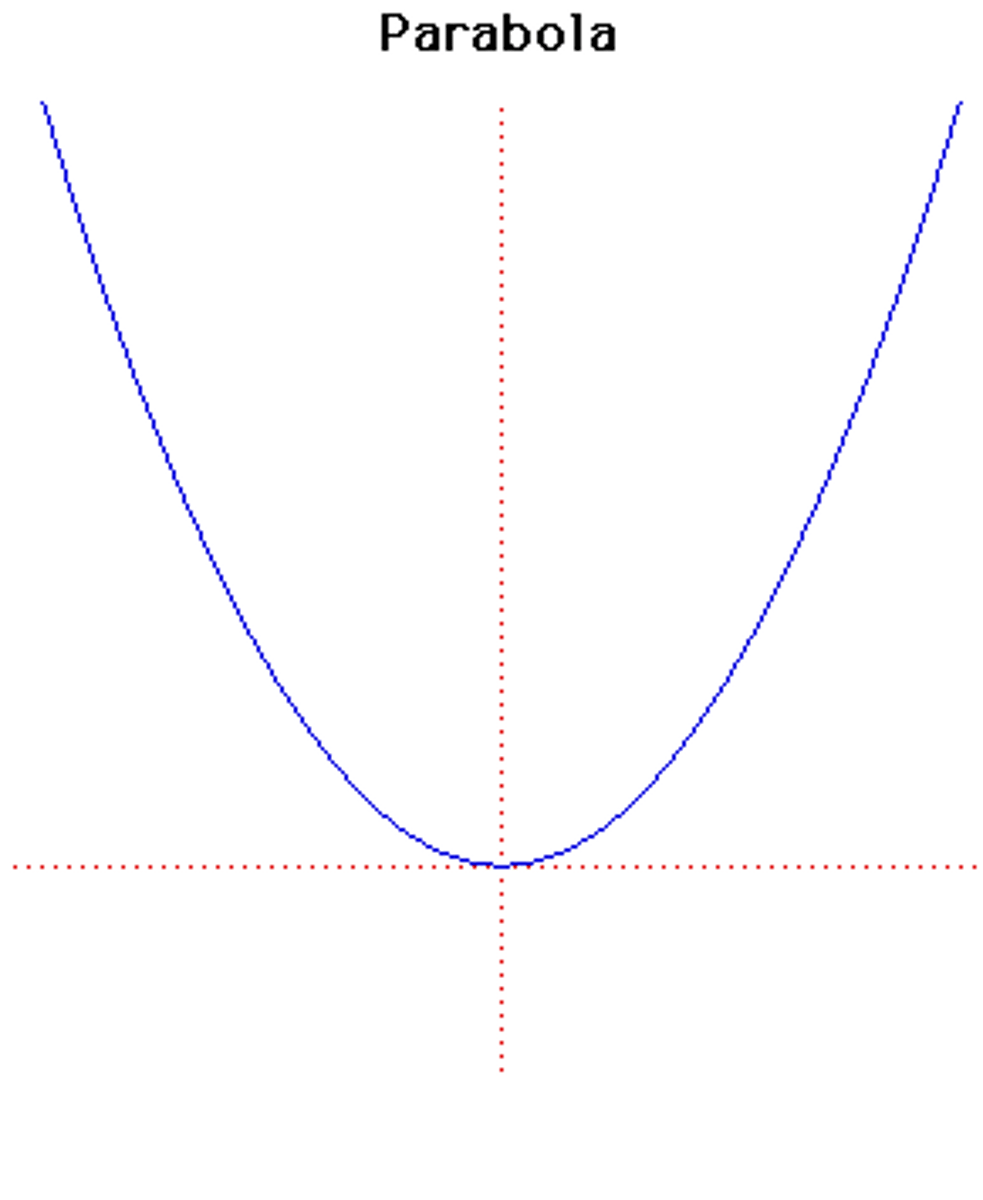
parabola

y = x2

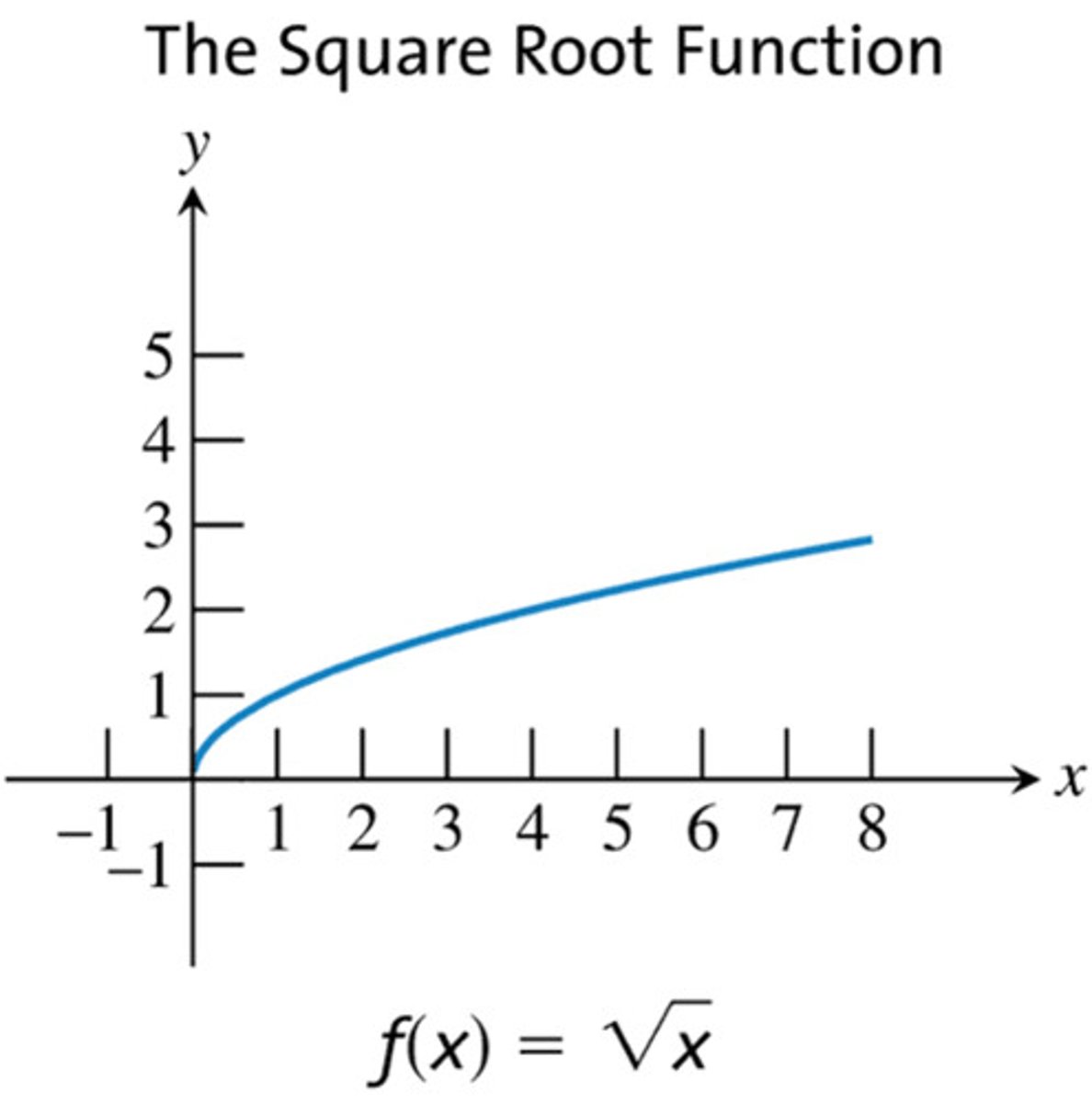
square root function

y = Square root of x

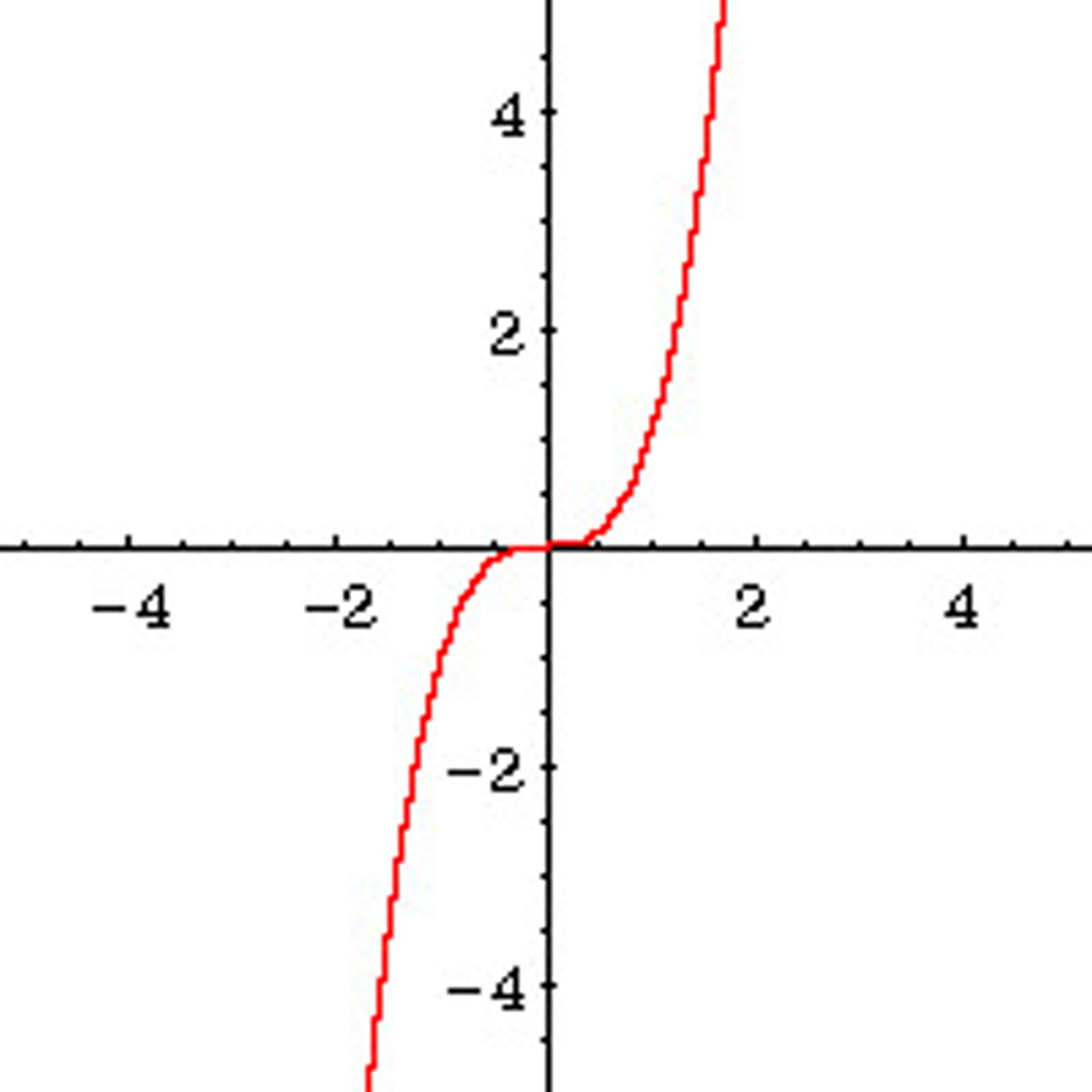
cubic function

y = x3

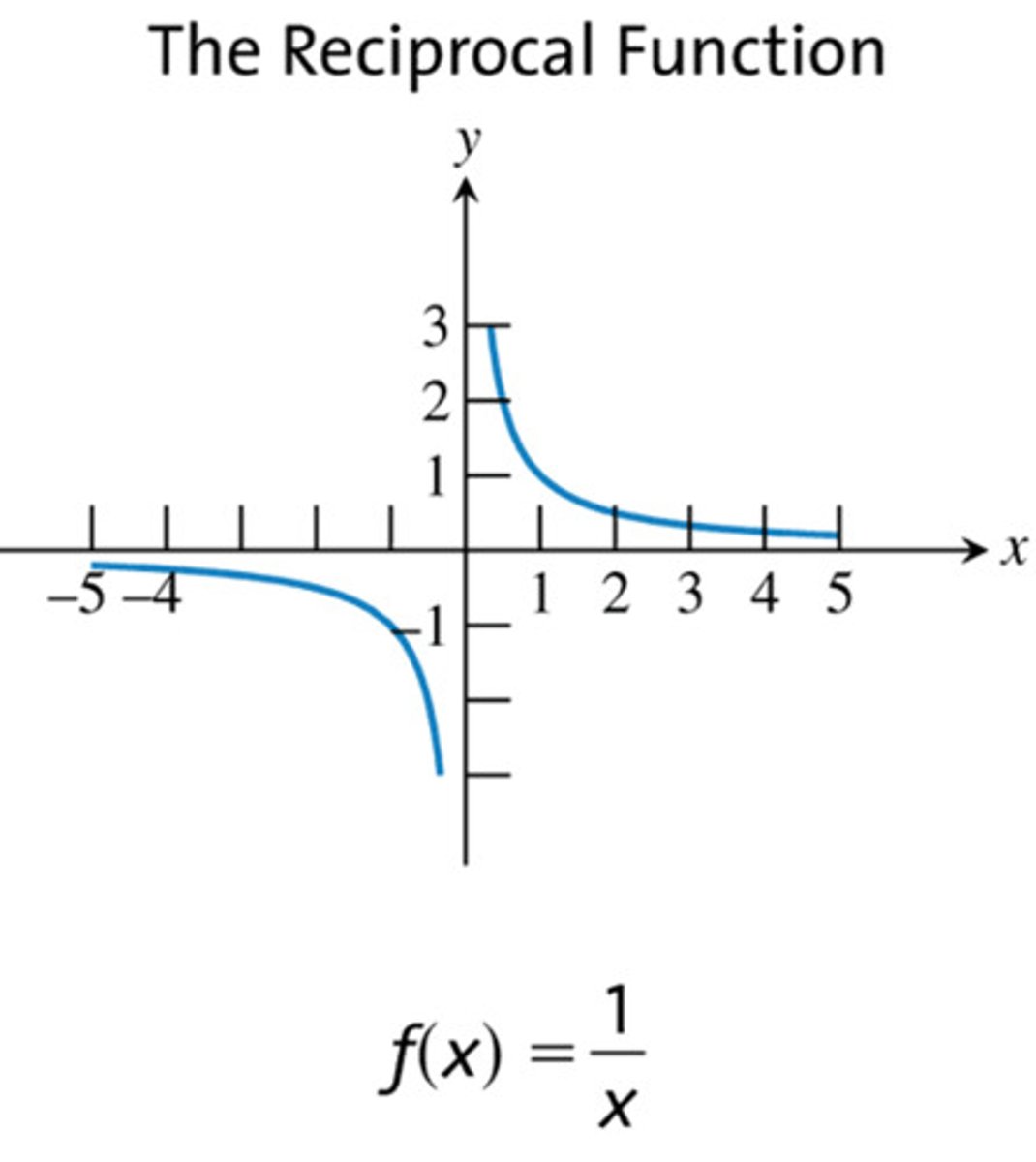
reciprocal function

y = 1/x

x-intercept

solution

y-intercept

constant

slope intercept form

y = ax + b

quadratic equation

ax2 + bx + c = 0

three methods for solving a quadratic equation

1. Factoring. 2. Completing the square.

3. The quadratic formula.

f(x) = x2 −2x −3

x-intercept are −1 and 3;y-intercept is −3

f(x) = x2 −10x + 25

double root is 5

construct the quadratic roots

The sum of the roots & their product

Construct the quadratic whose roots are 2 + iSquare root of 5, 2 − iSquare root of 5

The sum of the roots is 4. Their product is 4 − (iSquare root of 5)2 = 4 + 5 = 9.

Therefore, the quadratic is x2 − 4x + 9.

Construct the quadratic whose roots are 3 + Square root of 3, 3 − Square root of 3.

The sum of the roots is 6. Their product is 9 − 3 = 6.

Therefore, the quadratic is x2 − 6x + 6.

perfect square trinomial

a2 + 2ab + b2 = (a + b)2

completing the square

1) Transpose the constant term to the right

2) Add a square number to both sides. Add the square of half the coefficient of x.

3) The left-hand side is now the perfect square

The quadratic formula

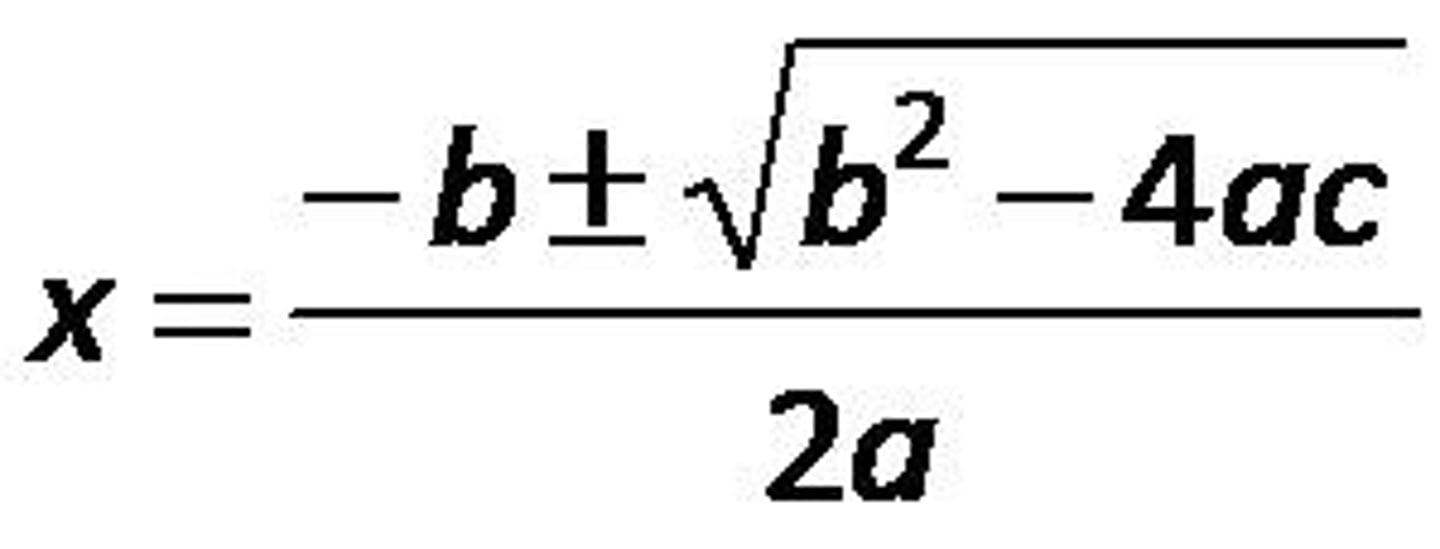
Dividend/Divisor

= Quotient + Remainder/Divisor

Dividend

= Quotient· Divisor + Remainder.

The remainder theorem

The value of a polynomial P(x) at x =a,

P(a), is equal to the remainder upon dividing P(x) by x − a

Use synthetic division to divide

x3 − 8x2 + x + 2 by x − 7.

(x2 − x − 6)(x − 7) − 40

The Factor Theorem

x − r is a factor of a polynomial P(x) if and only if r is a root of P(x)

Fundamental Theorem of Algebra

A polynomial of degree n has at least one root, real or complex.

The integer root theorem

If an integer is a root of a polynomial whose coefficients are integers and whose leading coefficient is ±1, then that integer is a factor of the constant term.

Conjugate pairs

If the irrational number a + Square root of b is a root, then its conjugate a − Square root of b is also a root.

Proof of the factor theorem

x − r is a factor of a polynomial P(x)

if and only if

r is a root of P(x).

If f(−x) = f(x),

then the graph of f(x) is symmetrical with respect to the y-axis

If f(−x) = −f(x)

then the graph of f(x) is symmetrical with respect to the origin.

even function

A function symmetrical with respect to the y-axis

odd function

A function that is symmetrical with respect to the origin

A polynomial will be an even function when all the exponents are

even

A polynomial will be an odd function when all the exponents are

odd

translation

rigid movement, vertically or horizontally.

absolute value function

y = |x|

If the graph of y= f(x) is translated a units horizontally and b units vertically, then the equation of the translated graph is

y − b = f (x − a)

Write the equation of the parabola whose vertex is at (1, 2)

y − 2 = (x − 1)2

Write the equation of the parabola whose vertex is at (−1, 2)

y − 2 = (x + 1)2

What are the coördinates of the vertex of this parabola?

y = x2 + 5

The vertex is at (0, 5)

equation of a circle

x2 + y2 = r2

Write the equation of the circle of radius 3, and center at the following point. (1, 2)

(x - 1)2 + (y - 2)2 = 9

Write the equation of the circle of radius 3, and center at the following point. (-1, -2)

(x + 1)2 + (y + 2)2 = 9

If the graph of y = f (x) is translated a units horizontally and b units vertically, then the equation of the translated graph is

y − b = f(x − a)

If we multiply f(x) by a number greater than 1 -- as in the graph in the center

then every y-value is stretched

But if we multiply f(x) by a number less than 1 -- as in the graph on the right

then every y-value is shrunk

A rational function is a quotient of

polynomials

rational function

y = g(x)/h(x)

What happens to the value of y when x is close to a singularity?

y becomes extremely large

asymptote

a straight line that a graph comes closer and closer to but never touches.

Where do we always find a vertical asymptote of a graph?

At a singularity

What does the equation of a vertical line look like?

x = A number.

Functions f(x) and g(x) are inverses of one another if:

f(g(x)) = x and g(f(x))= x

inverse

reverses the action of that function.

identity function

I(x) = x

logbx = n

bn = x

Write in exponential form: log(2)32 = 5

2^5 = 32

log(b)x + log(b)y

log(b)xy

log(b)x − log(b)y

log(b)x/y

n log(b)x

log(b)x^n

log(b)y = x

b^x = y

f(x)=AsinB(x-c) = 0

|A| = Amplitude of equation

C= Horizontal or phase shift

D= vertical shift

2(pie)/B= fundamental period

square pyramid surface surface area

area of base + 4(area of face)

tangent

= sin/cos

sin

= 1/cos

cot

cos/sin & 1/tan

csc

1/sin

cos

adjacent/hypotenuse

tan

opposite/adjacent

sec

hypotenuse/adjacent

sin

opposite/hypotenuse

cot

adj/opposite

csc

hypotenuse/opposite

sin-1 (inverse sine function)

Opposite / Hypotenuse

cos-1

adj/hypotenuse

tan-1

(Opposite / Adjacent) = θ

g(x)=−b∣x+h∣+g

b=shift

h=(-)horizontal shift

g=vertical shift