Teaching Symmetry (Session 3)

What is symmetry?

Symmetry is shared by mathematics, the natural world and art. Objects with symmetry seem more perfect that objects that don’t have symmetry.

There are three kinds of symmetry relevant to school geometry:

reflection symmetry (mirror or line symmetry), rotation symmetry and translation symmetry. We are going to focus on the first two types (line and rotational symmetry) - these are appropriate for primary education.

Line symmetry What is line symmetry?

A shape has line (also called reflection or mirror) symmetry if it can be reflected/flipped about a line so that it looks exactly the same as it did before reflecting.

Line symmetry can be verified by folding. It is possible to explore the line symmetry present in children's everyday life include nature, architecture and art as well as in 2-D shapes.

Use of context when teaching line symmetry

As always, it is essential to make the topic relevant to the pupils, linking with their lives and/or using an interesting context of interest to them. Consider the following:

OVER TO YOU! Find a letter with: • no lines of symmetry • one line of symmetry • two lines of symmetry • more than two lines of symmetry • a horizontal line of symmetry • a vertical line of symmetry • a diagonal line of symmetry Challenge: How many lines of symmetry in your name? What types? *The original document ‘Symmetry Shapes’ is available on the Moodle page for use in your teaching (download and save). 4. Examining the line symmetry in environment: Logos! What is a logo? A graphic representation or symbol of a company or other organisation often designed to be easily recognisable. Children will easily identify logos e.g. school crest, IRFU logo, Adidas logo, McDonalds logo, Nike logo etc. Here are some more:

Setting the scene:

All of the above contexts provide pupils will ample motivation to understand line symmetry. Here is an example of how this was done for the context of logos!

The student teacher introduced pupils to the marketing director of Iso-Ade, a fictitious sports drink company claiming to be an official sponsor of the next Summer Olympics, asks children to design a logo for their new drink: …Our isotonic sports drink keeps athletes hydrated even in the most competitive sporting event in the world, the Olympics. As marketing director, I am in charge of making people aware of our drink and how good it is. I am also in charge of the logo. A logo is a design that represents the company and helps people recognise their products. The best logos are the easiest to recognise. Everybody knows these logos [holding up logos for McDonalds and Nike*].

Research tells us that the best logos are symmetrical. Later you will help in selecting a logo for our company…but first you need to learn more about symmetry.

Note: This introduction provides the spring board to motivate children to want to learn more in order to be able to engage in this fun challenge. A similar approach could be taken for any sport e.g. GAA, hockey, etc. or national/international competition e.g. world cup, European championships etc. The assigned reading outlines how architecture could be used as a motivating context.

Supporting pupils in understanding line symmetry and how to teach

When teaching pupils about symmetry you must be confident in your teacher modelling (explanation and demonstration). The next sections support you in developing your teacher knowledge.

OVER TO YOU! • In simple terms, can you explain how you know when an item has line symmetry?

• How would you explain line symmetry to pupils? [keep it nice an simple]

Here are three children's different explanations of line symmetry: 'If something can fit perfectly in half, if you fold it in half and check if it’s perfectly onto itself with no bits sticking out'

'Symmetry is when you can fold something over horizontally or vertically and it’d be the exact same'

'…when a shape folds over equally on itself'

Teaching Line Symmetry

Pupils should be encouraged to predict whether an item has line symmetry (or not) and identify where the line(s) of symmetry might be.

They can test their predictions and find the line symmetry of various 2-D shapes using paper folding. how a teacher might introduce/review line symmetry with pupils, where paper folding is used.

Important teaching points outlined: Introducing line symmetry OVER TO YOU!

The template used in the video is the Symmetry Shapes handout available on the Moodle page. Print, cut the shapes out and predict and find the number of lines of symmetry for each shape: Watch this video, where after modelling, a pupil tests and identifies the line symmetry in various 2-D shapes: Pupil examining line symmetry For senior classes, you can challenge the pupils to predict the number of lines of symmetry prior to checking.

As appropriate, we can support pupils in identifying the numbers of lines of symmetry and making links with the strand unit Lines and Angles, by referring to vertical lines of symmetry, horizontal lines of symmetry and diagonal lines of symmetry.

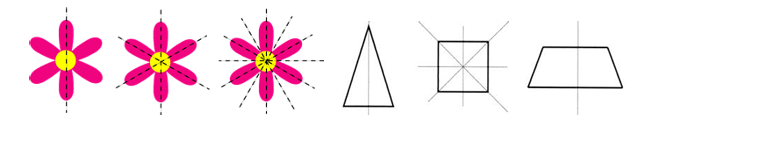
OVER TO YOU! This activity sheet shows the shapes that pupils explored. Each time the pupils worked in pairs, predicting how many lines of symmetry prior to folding the shapes to check. Predict the number of lines of symmetry and also the misconceptions/error pupils made.

Rotational symmetry What is rotational symmetry?

An object has rotational symmetry if when rotated around its centre point, the shape fits exactly onto its outline.

The number of time a shape fits exactly onto itself in one full rotation (i.e. 360 degrees) is called its order of symmetry.

The equilateral triangle (below) fits onto itself 3 times in one full rotation, it has rotational symmetry of 'order 3':

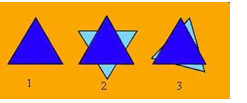
Using contexts

Teaching rotational symmetry

In order to teach this concept to the children, careful clear teacher modelling is essential. Watch the video to gain insights into how it is possible to find the rotational symmetry Introducing rotational symmetry

OVER TO YOU! The video showed how to find the rotational symmetry of a rectangle. Now, you select a different 2-D shape from the Symmetry Shapes template and find the rotational symmetry: Ensure you predict before you check. Remember, in preparation, you need to

1. Print two copies of the template. Have 2 copies of each shape (1 cut-out and 1 background shape) (see below).

2. Find the centre point

3. Mark a starting point (see below)

Ensure you find the rotational symmetry of the 3 remaining shapes on the template!

While it might seem straightforward, it is only through doing that maths concepts you get a full sense of what is required!

Fun fact!! A shape with rotational symmetry of order 1 (only fits onto itself once in one full rotation- i.e. at the starting point) is considered to have NO rotational symmetry.

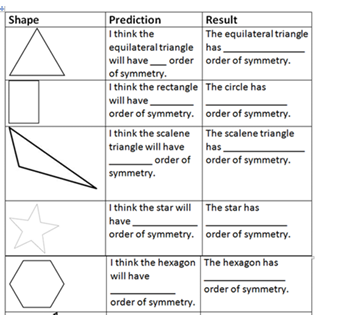
OVER TO YOU! Pupils predicted the rotational symmetry of the shapes below prior to checking. For each shape, predict the rotational symmetry as well as common errors pupils made.

Threading the context

In relation to the context of Logos, once children have learned all about symmetry (line and/or rotational symmetry), the context can be used to motivate pupils to use their knowledge:

1. Once pupils had learned about line symmetry and rotational symmetry, they examined the line and rotational symmetry in a number of popular logos (whole class activity):

2. Pupils were set a task. Again, this can be presented in the form of a letter, or alternatively you may have videoed a peer, who plays the role of the Marketing Director of ‘Isoade’: Welcome back. Now for the task: you must work in pairs to design a logo. Please follow the brief. First, you must pick an outline shape for the logo that has at least one line of symmetry and rotational symmetry of at least order

3. Once you have picked your outline shape make the logo attractive and colourful with a cool design. When you are finished, the entire logo should have line symmetry. The most creative and original logo will be chosen as the company’s official logo. Good luck. *Note: you can modify this task to make it more/less challenging for pupils.

3. Allow pupils to present their logos, focusing on its symmetry (example of pupils' work below):