21.11- Hypothesis testing. Null vs alternative (It's not from this course)
1/52
Earn XP
Description and Tags
This is from (365 Data Science). Source: (https://www.youtube.com/watch?v=ZzeXCKd5a18&ab_channel=365DataScience) P.S.: Also, This video has a lot of mistakes, but we will only include the right information for the questions below.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
53 Terms
Answer: B) The default or skeptical position that assumes no effect.
Explanation:
The null hypothesis (H₀) is the default assumption (e.g., "no difference," "no effect," or the opposite of the claim being tested). Researchers aim to reject H₀ in favor of the alternative (H₁).
In hypothesis testing, the null hypothesis (H₀) represents:
A) The researcher’s claim that they want to prove.
B) The default or skeptical position that assumes no effect.
C) The alternative scenario that challenges the status quo.
D) The hypothesis that is always rejected.
Answer: B) H₀: μ ≤ $125k; H₁: μ > $125k
Explanation:
H₀ must be the skeptical position (salaries ≤ $125k), and H₁ is Paul’s claim (> $125k). Rejecting H₀ supports Paul’s claim.
Paul claims that data scientists earn more than $125,000/year. How should H₀ and H₁ be set up to test this?
A) H₀: μ > $125k; H₁: μ ≤ $125k
B) H₀: μ ≤ $125k; H₁: μ > $125k
C) H₀: μ = $125k; H₁: μ ≠ $125k
D) H₀: μ ≥ $125k; H₁: μ < $125k
Answer: D) All of the above.
Explanation:
(A) Rejecting H₀: μ > $125k would mean concluding μ ≤ $125k (opposite of Paul’s claim).
(B) H₀ must include equality (e.g., ≤, =, or ≥).
(C) Failing to reject H₀ is weak—it doesn’t prove > $125k.
Why is it incorrect to set H₀: μ > $125k when testing Paul’s claim?
A) Because rejecting H₀ would disprove Paul’s claim.
B) Because H₀ must always include an equality (≤, =, or ≥).
C) Because failing to reject H₀ doesn’t provide evidence for Paul’s claim.
D) All of the above.
Answer: C) There’s significant evidence that salaries are > $125k.
Explanation:
Rejecting H₀: μ ≤ $125k means the data supports the alternative (H₁: μ > $125k), aligning with Paul’s claim.
What does it mean if you reject H₀: μ ≤ $125k (p < 0.05)?
A) There’s evidence that salaries are ≤ $125k.
B) There’s insufficient evidence to support Paul’s claim.
C) There’s significant evidence that salaries are > $125k.
D) The test is inconclusive.
Answer: B) Researchers aim to reject H₀ to support their hypothesis.
Explanation:
(A) False: Failing to reject H₀ doesn’t prove it; it just means insufficient evidence.
(B) True: Researchers reject H₀ to support H₁.
(C) False: H₁ never includes equality (e.g., >, <, or ≠).
(D) False: H₀ is the default ("boring") position; H₁ is the exciting claim.
Which statement about hypothesis testing is TRUE?
A) Failing to reject H₀ proves H₀ is true.
B) Researchers aim to reject H₀ to support their hypothesis.
C) H₁ always includes an equality (e.g., =, ≤, or ≥).
D) The null hypothesis is usually the exciting, new claim.
Answer: B) Two-tailed (non-directional)
Explanation:
H₁: μ ≠ $113k checks for differences in either direction (higher or lower), making it a two-tailed test.
If you set H₀: μ = $113k and H₁: μ ≠ $113k, what type of test is this?
A) One-tailed (directional)
B) Two-tailed (non-directional)
C) Null-tailed
D) Alternative-tailed
Answer: B ("The mean exam score is at least 80.")
Explanation:
H₀ must be a testable statistical statement with a population parameter (e.g., μ ≥ 80). Qualitative claims (A, D) or effect sizes (C) are not valid H₀ forms.
Which of the following is a valid null hypothesis (H₀)?
A) Cats are better than dogs.
B) The mean exam score is at least 80.
C) The new drug increases cure rates by 20%.
D) People prefer chocolate ice cream.
Answer: C (Two-tailed)
Explanation:
H₁: μ ≠ 50 checks for differences in both directions (higher or lower than 50), requiring a two-tailed test.
If H₀: μ = 50 and H₁: μ ≠ 50, what type of test is this?
A) One-tailed (left-tailed)
B) One-tailed (right-tailed)
C) Two-tailed
D) Non-directional
Answer: B) Reject H₀
Explanation:
If p-value < α (0.03 < 0.05), reject H₀. Note: We never "accept H₁"—we only find evidence against H₀.
A p-value of 0.03 in a test with α = 0.05 implies:
A) Fail to reject H₀.
B) Reject H₀.
C) Accept H₁.
D) The test is inconclusive.
Answer: A) Concluding salaries > $125k when they are ≤ $125k.
Explanation:
Type I error = False positive. Here, it’s rejecting a true H₀ (incorrectly concluding > $125k when reality is ≤ $125k).
What is the Type I error in testing Paul’s salary claim (H₀: μ ≤ $125k)?
A) Concluding salaries > $125k when they are ≤ $125k.
B) Concluding salaries ≤ $125k when they are > $125k.
C) Failing to reject H₀ when it’s false.
D) Accepting H₀ when it’s true.
Answer: D) H₁ can include equality.
Explanation:
H₁ never includes equality (e.g., it’s >, <, or ≠). H₀ must include equality (A is true). B and C are correct.
Which statement about H₀ and H₁ is FALSE?
A) H₀ always includes equality (=, ≤, or ≥).
B) H₁ is the hypothesis researchers want to prove.
C) H₀ and H₁ must cover all possible outcomes.
D) H₁ can include equality.
Answer: A) Increases
Explanation:
Lower α makes it harder to reject H₀, increasing the chance of failing to reject a false H₀ (Type II error).
If you set α = 0.01 (instead of 0.05), what happens to the risk of Type II error?
A) Increases
B) Decreases
C) Stays the same
D) Depends on the sample size
Answer: C) On the right side
Explanation:
A one-tailed test with ">" places the critical region in the right tail of the distribution (only high values reject H₀).
In a one-tailed test (H₁: μ > 100), the critical region is:
A) On both sides of the distribution.
B) On the left side.
C) On the right side.
D) Nowhere; one-tailed tests don’t have critical regions.
Answer: A) Reject H₀ at α = 0.05
Explanation:
Since 115 is outside the 95% CI (120, 130), we reject H₀: μ = 115 (p < 0.05).
A 95% confidence interval for μ is (120, 130). What can you conclude about H₀: μ = 115?
A) Reject H₀ at α = 0.05.
B) Fail to reject H₀ at α = 0.05.
C) Accept H₀ at α = 0.05.
D) The interval is irrelevant to H₀.
Answer: B) The probability of correctly rejecting a false H₀.
Explanation:
Power = 1 − P(Type II error). It’s the chance of correctly detecting an effect (rejecting false H₀).
Power in hypothesis testing refers to:
A) The probability of rejecting H₀ when it’s true.
B) The probability of correctly rejecting a false H₀.
C) The probability of accepting H₁.
D) The probability of Type II error.
Answer: D) All of the above.
Explanation:
Pre-specifying hypotheses prevents data dredging and ensures unbiased, reproducible conclusions.
Why is it important to pre-specify H₀ and H₁ before collecting data?
A) To avoid p-hacking (fishing for significant results).
B) To reduce bias in interpreting results.
C) To align with the scientific method.
D) All of the above.
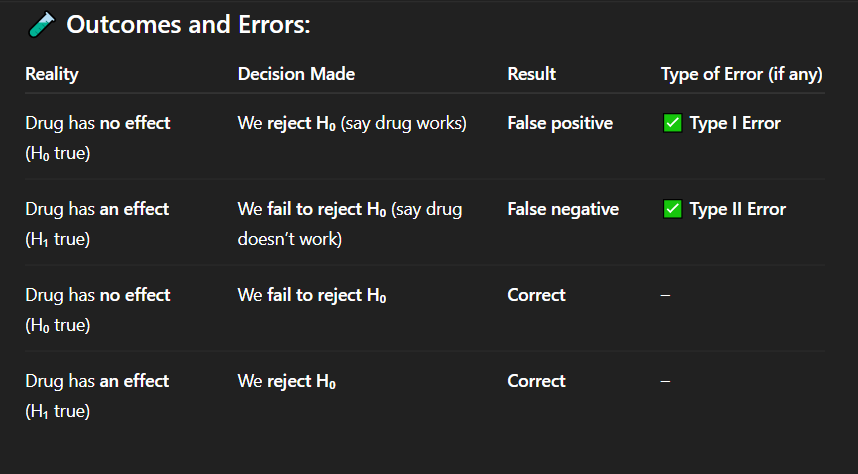
Answer: B) Fail to detect that the drug works when it actually does
Explanation:
Type II error (β) = Failing to reject a false H₀. Here, it means missing the drug’s true effect.
In a clinical trial testing a new drug (H₀: drug has no effect), a Type II error occurs when researchers:
A) Conclude the drug works when it doesn’t
B) Fail to detect that the drug works when it actually does
C) Reject H₀ when it’s true
D) Use a two-tailed test instead of a one-tailed test
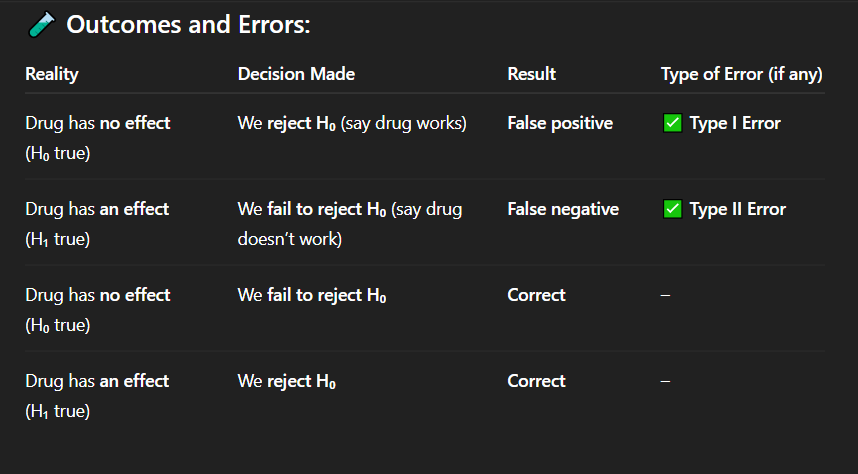
Answer: B) P(Type II error) is low
Explanation:
High power = 1 − P(Type II error). Power increases with larger effect sizes or sample sizes.
If a test has high power, which of the following is true?
A) P(Type I error) is low
B) P(Type II error) is low
C) The effect size is small
D) The sample size is small
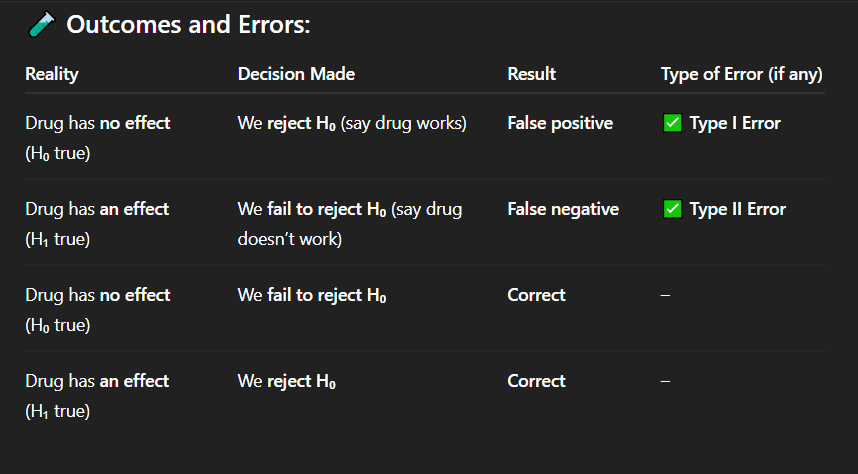
Answer: B) Fail to reject H₀ at α = 0.05
Explanation:
Since 10 is within the CI (9.8, 10.3), we fail to reject H₀ (p > 0.05).
A researcher tests H₀: μ = 10 vs. H₁: μ ≠ 10 and obtains a 95% CI of (9.8, 10.3). What should they conclude?
A) Reject H₀ at α = 0.05
B) Fail to reject H₀ at α = 0.05
C) Accept H₁
D) The test is inconclusive
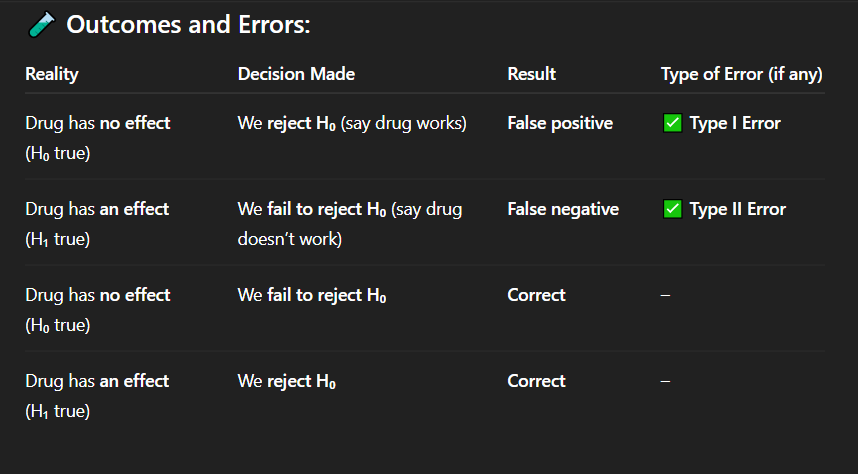
Answer: C) Increasing the effect size
Explanation:
Power ↑ with:
Larger effect size
Larger sample size
Higher α (e.g., 0.05 vs. 0.01)
One-tailed tests (when appropriate)
Which of the following would increase the power of a test?
A) Decreasing α from 0.05 to 0.01
B) Reducing the sample size
C) Increasing the effect size
D) Using a two-tailed test instead of one-tailed
Answer: C) Marginal significance requiring replication
Explanation:
p > α means fail to reject H₀, but p close to α (e.g., 0.07) suggests marginal results worth further study.
A p-value of 0.07 with α = 0.05 implies:
A) Statistically significant results
B) Clinically significant results
C) Marginal significance requiring replication
D) Proof that H₀ is true
Answer: A) When H₁ specifies a direction (e.g., μ > 100)
Explanation:
One-tailed tests are for directional hypotheses (e.g., ">", "<"). Two-tailed tests are for "≠".
When should a one-tailed test be used?
A) When H₁ specifies a direction (e.g., μ > 100)
B) When the sample size is small
C) When the data is normally distributed
D) When testing for any difference (μ ≠ 100)
Answer: B) 5% chance of rejecting a true H₀
Explanation:
α = P(Type I error) = P(reject H₀ | H₀ is true). It is not the probability H₀ is true.
Which is a correct interpretation of α = 0.05?
A) 5% chance H₀ is true
B) 5% chance of rejecting a true H₀
C) 95% chance H₁ is true
D) 5% chance of a Type II error
Answer: A) Type I error
Explanation:
Type I error = False positive = Rejecting a true H₀.
If H₀ is true but you reject it, you’ve made a:
A) Type I error
B) Type II error
C) Correct decision
D) Power error
Answer: C) Choice of H₁
Explanation:
Power depends on:
Sample size (↑n → ↑power)
Effect size (↑effect → ↑power)
Data variability (↑σ → ↓power)
But not the formulation of H₁.
Which factor does NOT affect power?
A) Sample size
B) Effect size
C) Choice of H₁
D) Variability in data
Correct Answer: B) The status quo or default assumption
Explanation: The null hypothesis (H₀) should always represent the default or skeptical position (e.g., "no effect," "no difference," or "≤ a threshold"). The alternative hypothesis (H₁) is the claim you test against it.
What should the null hypothesis (H₀) typically represent?
A) The new claim you want to prove
B) The status quo or default assumption
C) The opposite of what you believe
D) A guess with no statistical meaning
Correct Answer: D) Both A and C
Explanation:
H₀ must include equality (e.g., ≤, ≥, or =).
If H₀ is "> $125k," failing to reject it doesn’t prove Paul is right—it just means you lack evidence to disprove him.
Why is it incorrect to set H₀ as "Mean salary > $125k" when testing Paul’s claim?
A) Because H₀ must always include an equality (=, ≤, ≥)
B) Because you can never reject H₀
C) Because it makes it impossible to statistically support Paul’s claim
D) Both A and C
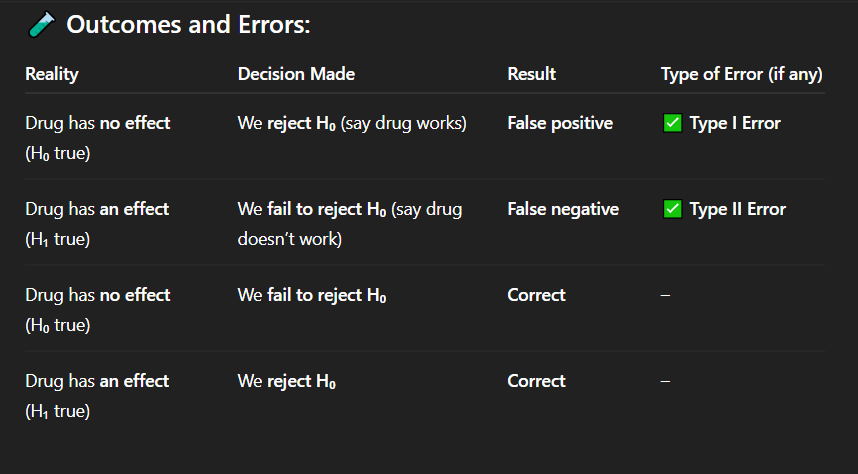
Correct Answer: A) Reject H₀ (evidence supports H₁)
Explanation: If p-value < α, you reject H₀. Here, 0.03 < 0.05 means statistically significant evidence for the alternative hypothesis (H₁).
If your p-value is 0.03 and α = 0.05, what should you conclude?
A) Reject H₀ (evidence supports H₁)
B) Fail to reject H₀ (no evidence for H₁)
C) Accept H₀ (H₀ is true)
D) The test is inconclusive
Correct Answer: A) Increases
Explanation: Lower α makes it harder to reject H₀, so you’re more likely to miss a true effect (Type II error).
Salary example: With α = 0.01, you might fail to reject *"≤ 125k"∗ even if the true mean is 130k.
If you set α = 0.01 (instead of 0.05), what happens to the risk of Type II error?
A) Increases
B) Decreases
C) Stays the same
D) Depends on sample size
Correct Answer: B) You want to detect any difference (stronger or weaker)
Explanation: Two-tailed tests check for any difference (≠). One-tailed tests check for a specific direction (> or <).
Example:
One-tailed: "Is Lightning > Fire?"
Two-tailed: "Is Lightning’s DPS different from Fire’s (better or worse)?"
A two-tailed test is appropriate when:
A) You only care if Lightning is stronger than Fire
B) You want to detect any difference (stronger or weaker)
C) Your p-value is exactly 0.05
D) H₀ includes a strict equality (e.g., μ = $125k)
Correct Answer: B) Fail to reject H₀ but recommend more testing
Explanation: If p > α, you fail to reject H₀ (no significant evidence). But you can’t "accept" H₀—you might need more data.
Salary analogy: You can’t prove
“average salary ≤ 125k”, but you also can’t support
“average salary >125k” yet.
If your test’s p-value = 0.07 and α = 0.05, which action aligns with statistical best practices?
A) Reject H₀ and declare significance
B) Fail to reject H₀ but recommend more testing
C) Change α to 0.10 to force significance
D) Accept H₀ as proven true
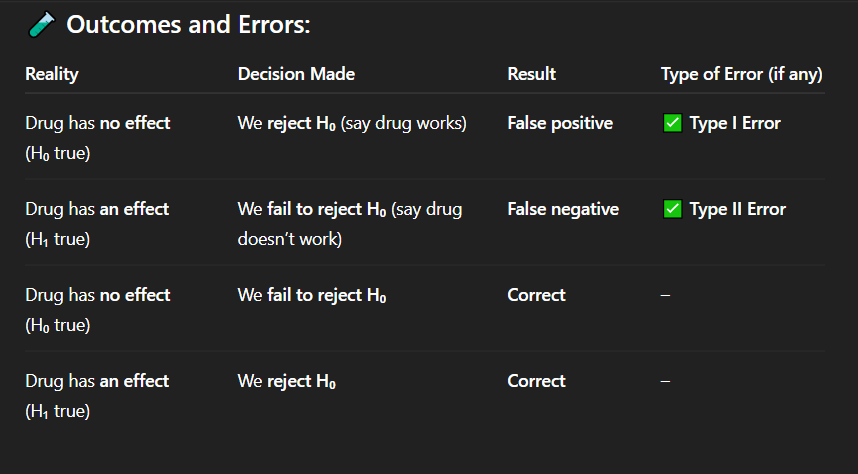
Correct Answer: A) The probability of correctly rejecting H₀ when H₁ is true
Explanation: Power = 1 – P(Type II error). It’s the test’s ability to detect an effect if it exists.
Dark Souls analogy: Power is like your build’s ability to reliably detect if Lightning is better (e.g., by fighting the boss 50 times vs. 5 times).
Power in hypothesis testing refers to:
A) The probability of correctly rejecting H₀ when H₁ is true
B) The chance of making a Type I error
C) The p-value threshold (α)
D) The effect size needed for significance
Correct Answer: B) Increase the sample size of data scientist salaries
Explanation: Larger samples reduce noise, making it easier to detect true effects.
Key trade-offs:
α (e.g., 0.01) reduces power (harder to reject H₀).
One-tailed tests increase power for directional hypotheses (vs. two-tailed).
To increase power in the salary test (H₁: μ > $125k), you could:
A) Reduce α from 0.05 to 0.01
B) Increase the sample size of data scientist salaries
C) Change H₀ to μ = $125k
D) Use a one-tailed test instead of two-tailed
Correct Answer: C) Cohen’s d measures it in standard deviations
Explanation:
Cohen’s d quantifies effect size (e.g., "Lightning deals 0.8 SD more DPS than Fire").
Misconceptions:
Effect size ≠ p-value (p-values depend on sample size; effect sizes don’t).
Small effect sizes can be significant with huge samples (and vice versa).
Which statement about effect size is true?
A) It’s determined by the p-value
B) It’s independent of sample size
C) Cohen’s d measures it in standard deviations
D) A large effect size guarantees statistical significance
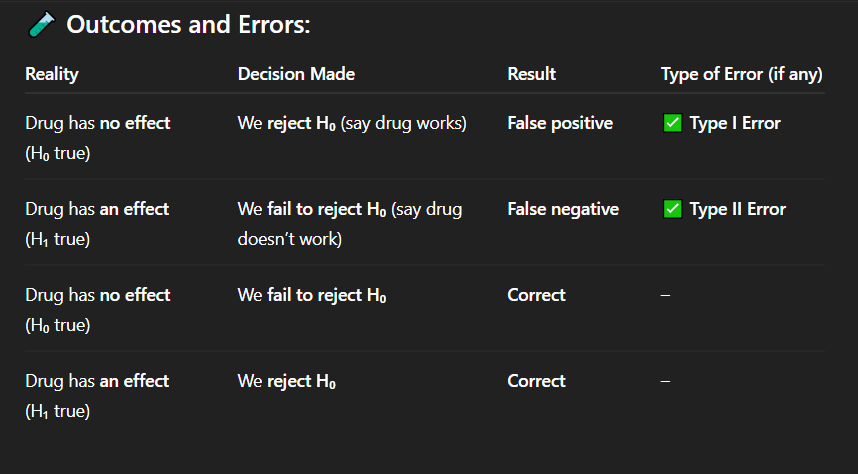
Correct Answer: B) 64%
Explanation:
P(At least 1 Type I error) = 1 – P(No errors) = 1 – (0.95)^20 ≈ 64%.
Lesson: Multiple testing increases false positives (use corrections like Bonferroni!).
If you conduct 20 hypothesis tests at α = 0.05, what’s the approximate probability of at least one Type I error (false positive)?
A) 5%
B) 64%
C) 95%
D) 100%
Correct Answer: B
Explanation: A Type I error occurs when the null hypothesis is actually true, but we incorrectly reject it — a false positive.
What is a Type I error in hypothesis testing?
A. Failing to reject a false null hypothesis
B. Rejecting a true null hypothesis
C. Rejecting a false null hypothesis
D. Accepting a true alternative hypothesis
Correct Answer: C) Failing to reject the null hypothesis when it is false
Explanation: A Type II error is when the null hypothesis is actually false, but we fail to reject it — a false negative.
Which of the following best describes a Type II error?
A. Rejecting the null hypothesis when it is true
B. Accepting the alternative hypothesis when it is false
C. Failing to reject the null hypothesis when it is false
D. Rejecting the null hypothesis when it is false
Correct Answer: C. Concluding the drug is effective when it is not
Explanation: Type I error means falsely concluding the drug works (rejecting H₀) when in reality it does not.
In the context of testing a new drug’s effectiveness, which of the following is an example of a Type I error?
A. Concluding the drug is ineffective when it actually is
B. Concluding the drug is effective when it actually is
C. Concluding the drug is effective when it is not
D. Concluding the drug is ineffective when it is not
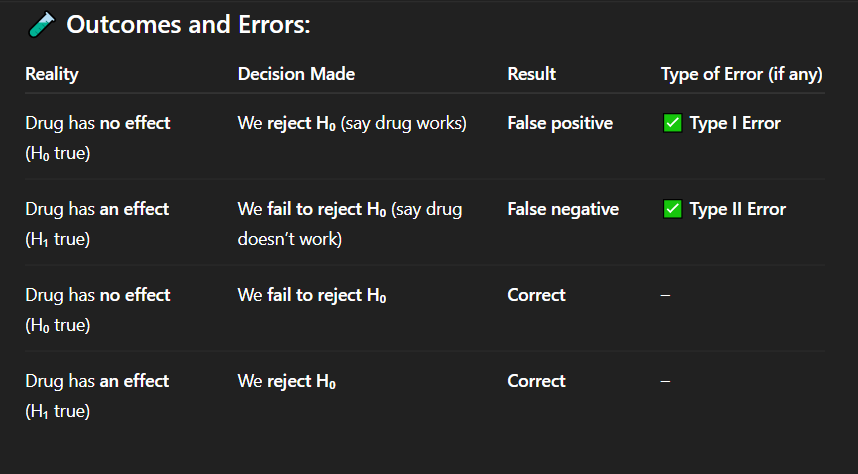
Correct Answer: C. The drug has no effect on blood pressure
Explanation: The null hypothesis assumes no change or no effect — in this case, that the drug does not affect blood pressure.
What is the null hypothesis (H₀) in a study testing whether a new drug reduces blood pressure?
A. The drug reduces blood pressure
B. The drug increases blood pressure
C. The drug has no effect on blood pressure
D. The drug is harmful
Correct Answer: C. H₀ is false, and we reject it
Explanation: When the null hypothesis is false and we reject it, that’s a correct and desired decision — we correctly identified an effect.
Which of the following scenarios represents a correct decision in hypothesis testing?
A. H₀ is false, and we fail to reject it
B. H₀ is true, and we reject it
C. H₀ is false, and we reject it
D. H₀ is true, and we reject it
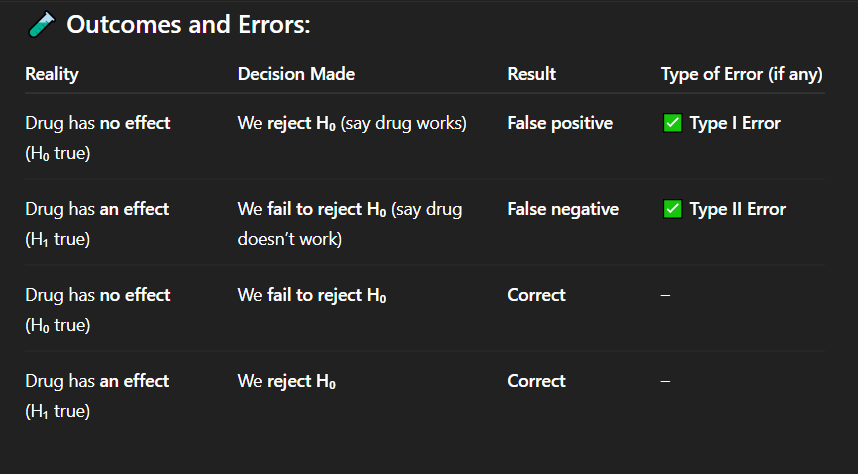
Correct Answer: C. There is a statistically significant effect or difference
Explanation: The alternative hypothesis suggests that there is a real, statistically significant effect or difference in the population.
Which of the following best describes the alternative hypothesis (H₁)?
A. There is no effect or difference
B. The result occurred due to chance
C. There is a statistically significant effect or difference
D. The study was biased
Correct Answer: C. There is not enough evidence to support the alternative hypothesis
Explanation: Failing to reject the null means the evidence was not strong enough to support the alternative — it does not prove the null is true.
What does it mean to "fail to reject the null hypothesis"?
A. The null hypothesis is definitely true
B. The alternative hypothesis is false
C. There is not enough evidence to support the alternative hypothesis
D. A Type I error has occurred
Correct Answer: B. Concluding a medication is ineffective when it actually is
Explanation: A Type II error is a false negative — failing to detect a true effect (in this case, that the medication works).
Which of the following situations describes a Type II error in a medical study?
A. Concluding a medication is effective when it’s not
B. Concluding a medication is ineffective when it actually is
C. Using the wrong statistical test
D. Measuring the wrong variable
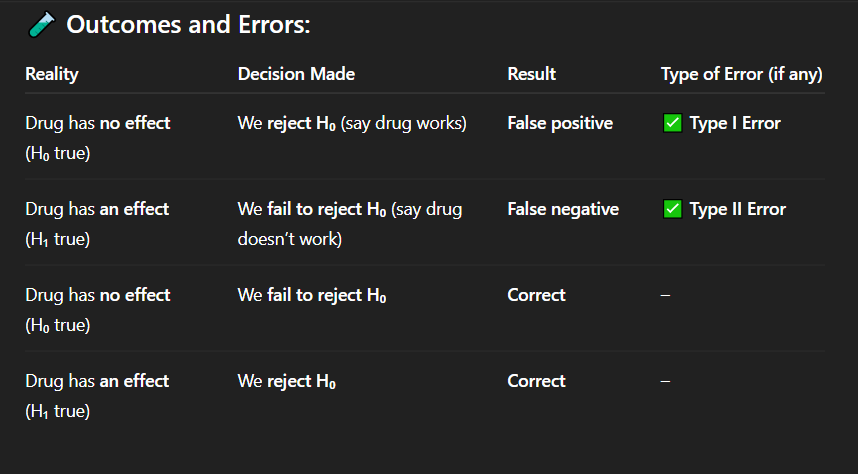
Correct Answer: C. There is a 5% chance of making a Type I error
Explanation: The significance level (alpha) is the probability of making a Type I error — rejecting a true null hypothesis.
If the significance level (α) is set to 0.05, what does this mean?
A. There is a 5% chance of accepting the null hypothesis
B. There is a 5% chance of making a Type II error
C. There is a 5% chance of making a Type I error
D. There is a 95% chance the null hypothesis is false
Correct Answer: D. Reducing Type I error risk may increase the chance of a Type II error
Explanation: There's often a trade-off — reducing the chance of a Type I error (e.g., lowering α) can increase the chance of a Type II error if the sample size is unchanged.
Which of the following statements is true about Type I and Type II errors?
A. Decreasing the chance of a Type I error also decreases the chance of a Type II error
B. Increasing the sample size increases both Type I and Type II errors
C. Type I and Type II errors are unrelated
D. Reducing Type I error risk may increase the chance of a Type II error
Correct Answer: B
Explanation: This is a Type I error — falsely rejecting a true null hypothesis (false positive).
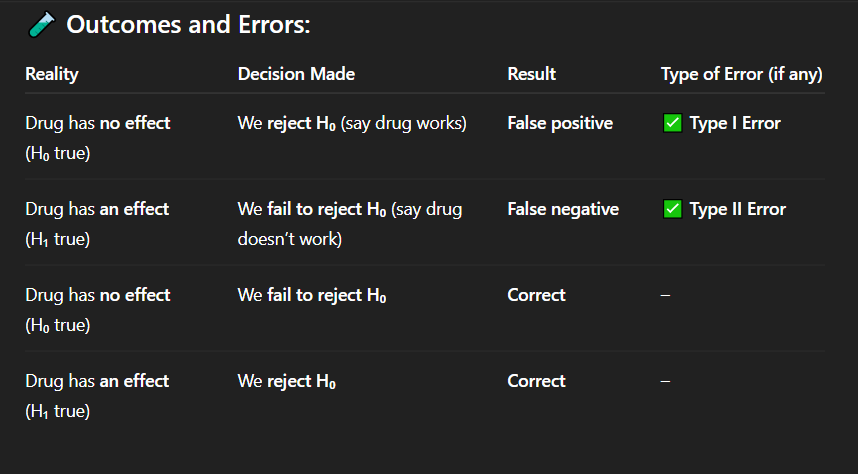
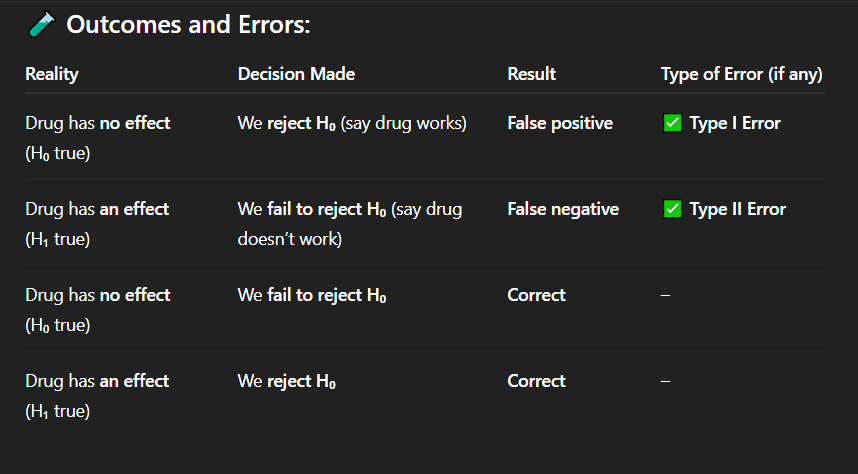
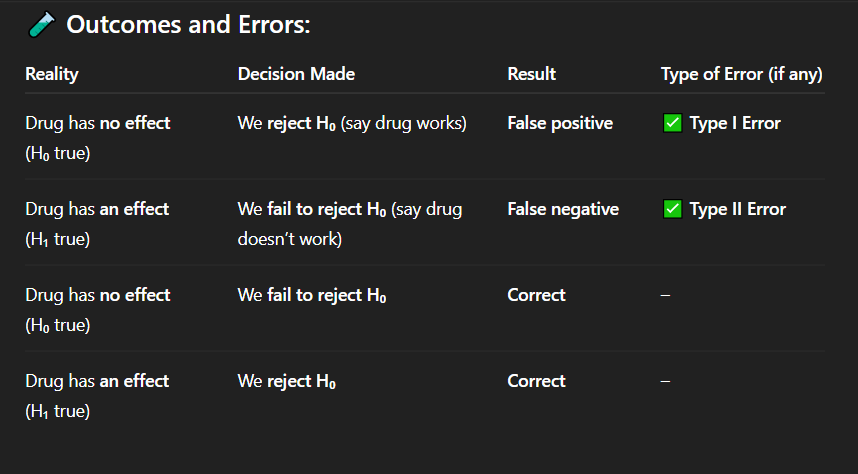
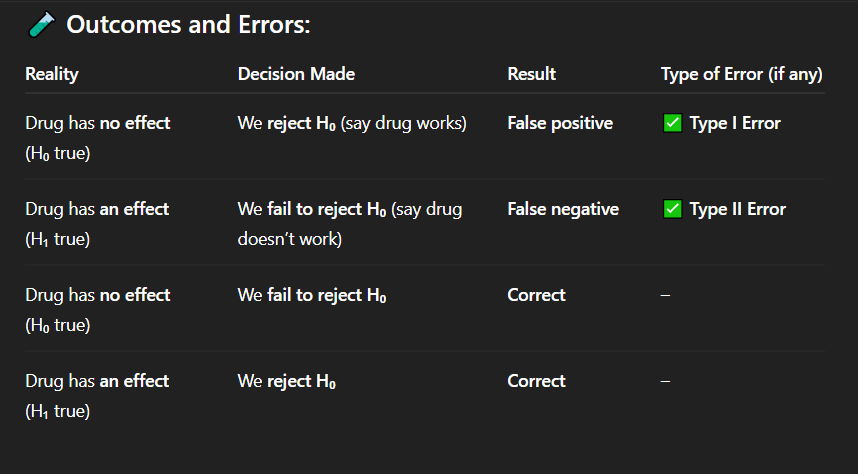
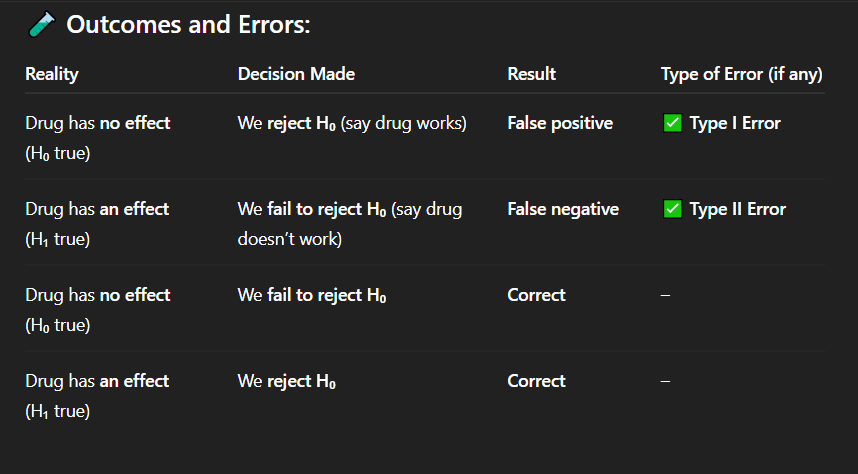
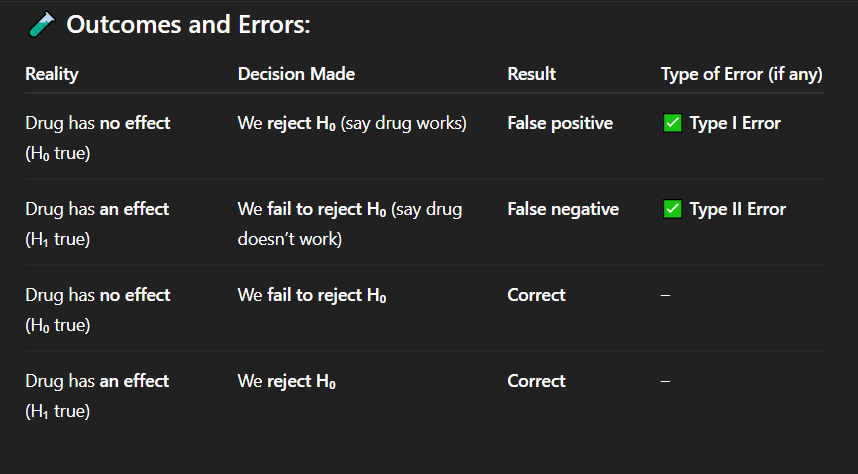
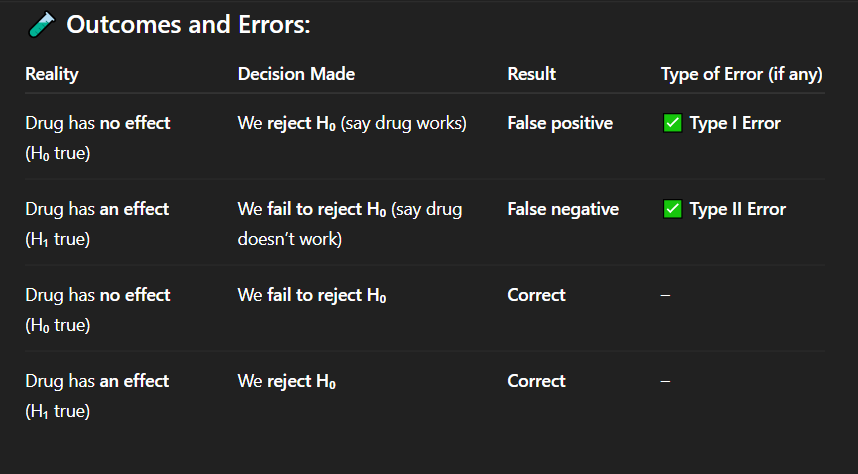
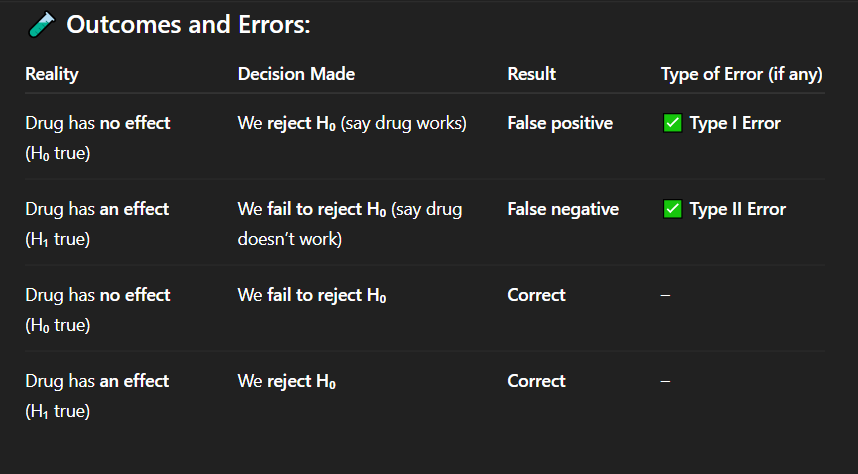
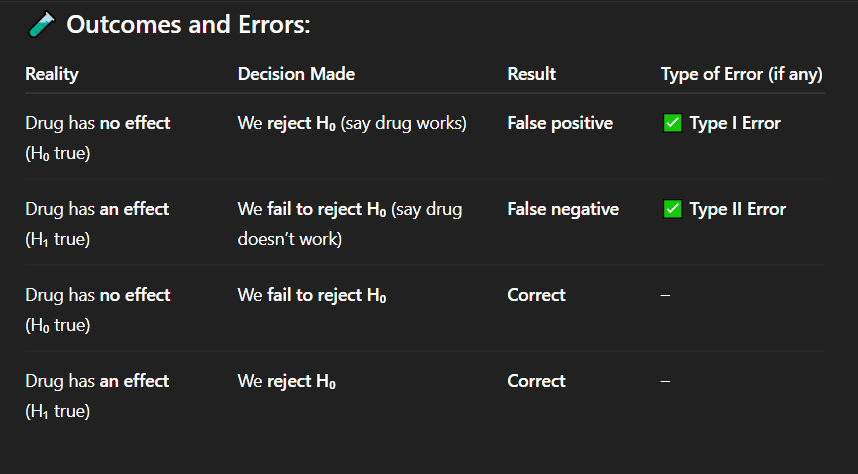
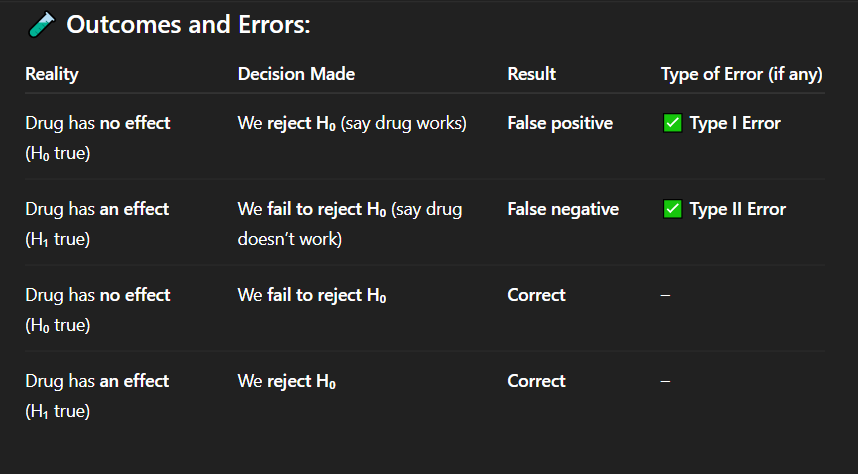
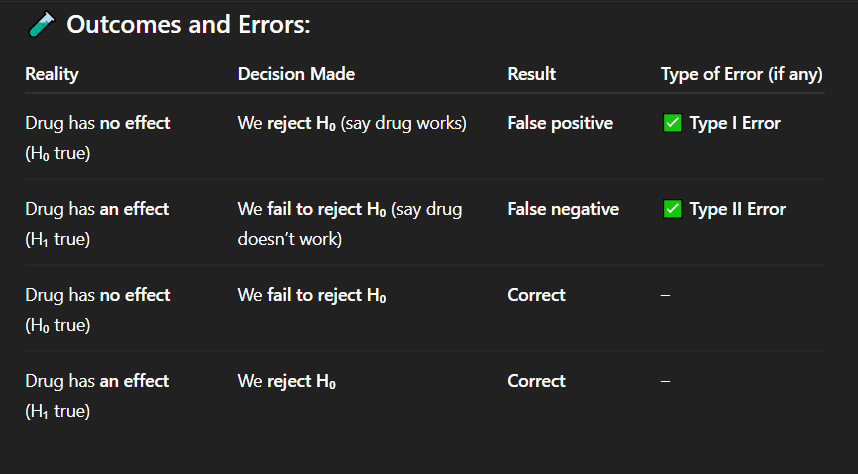
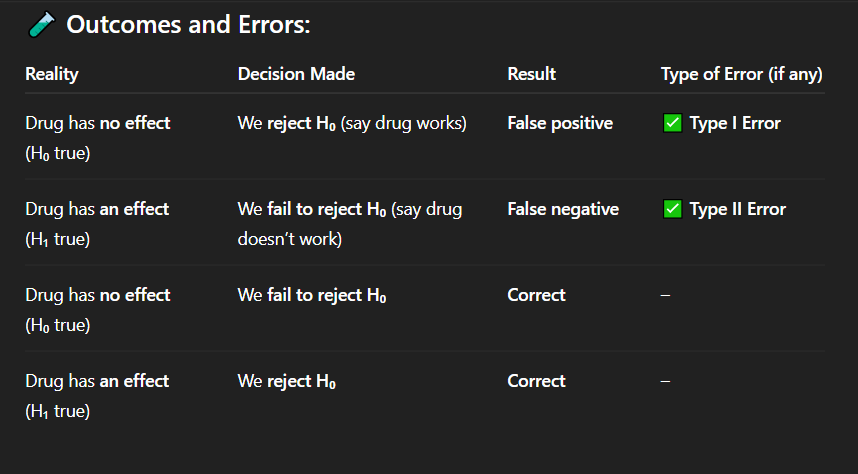
If the drug actually has no effect, but researchers conclude that it works, what type of error has occurred?
A. No error
B. Type I error
C. Type II error
D. Type III error
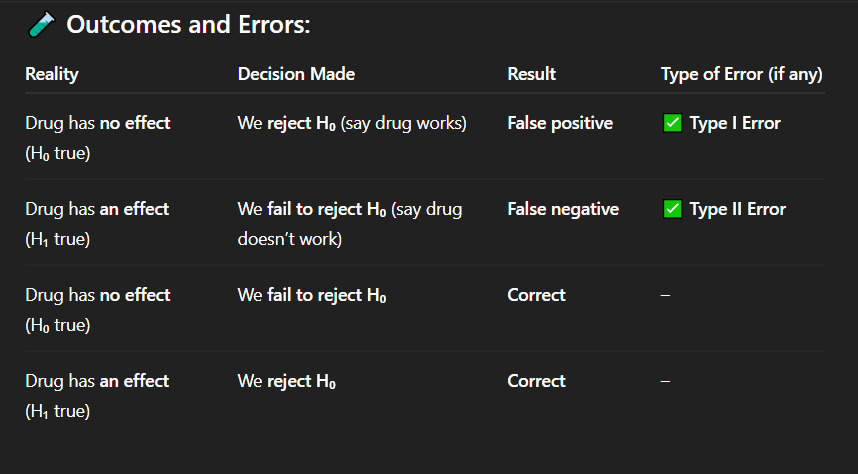
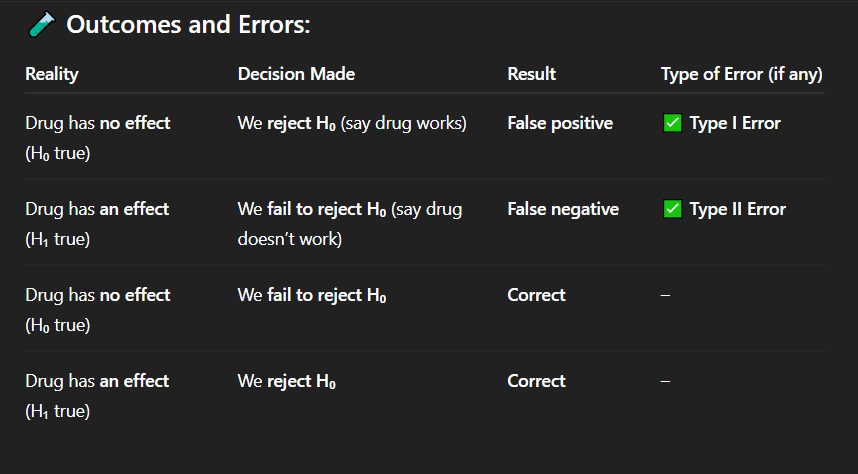
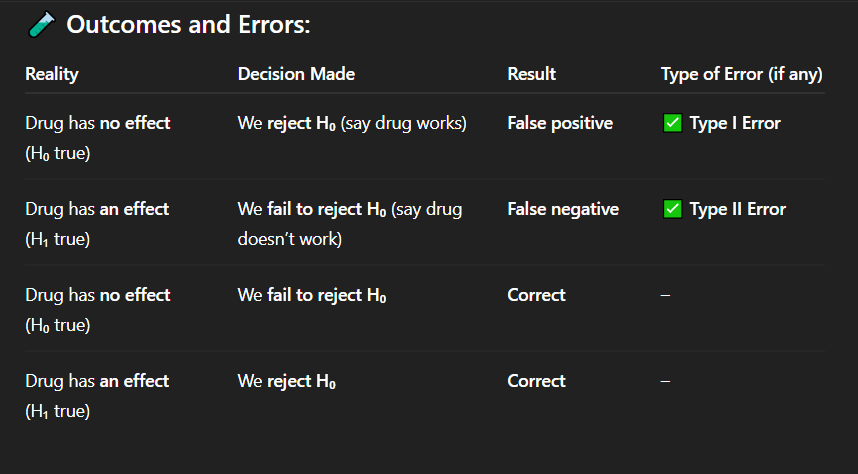
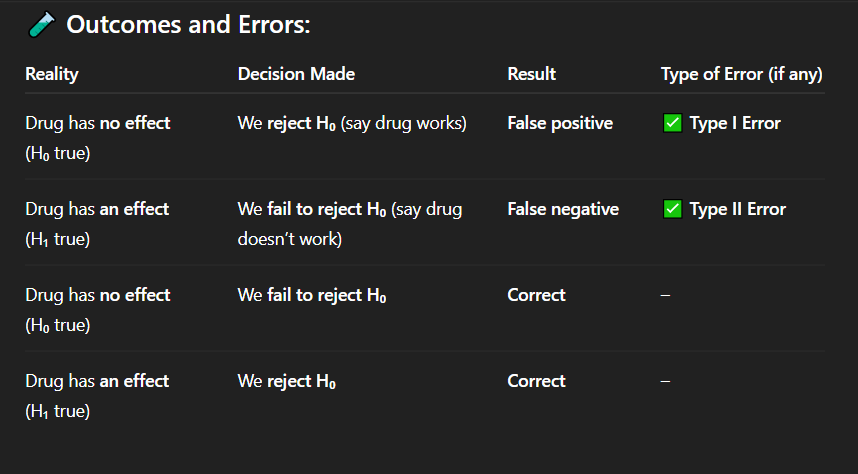
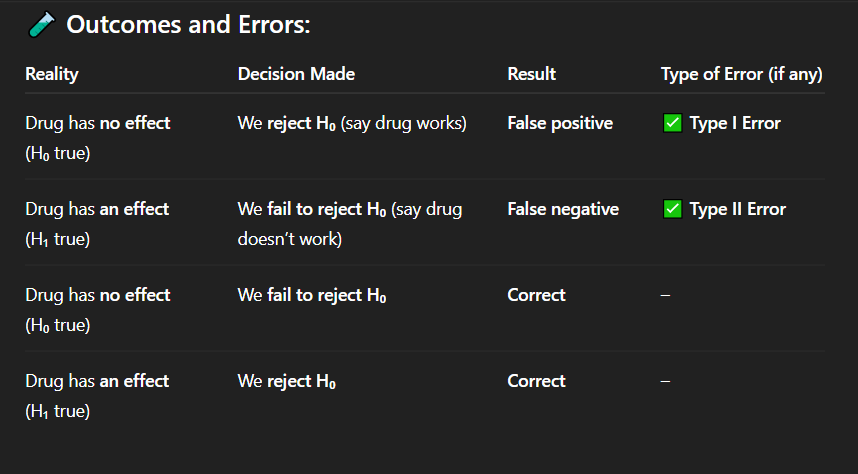
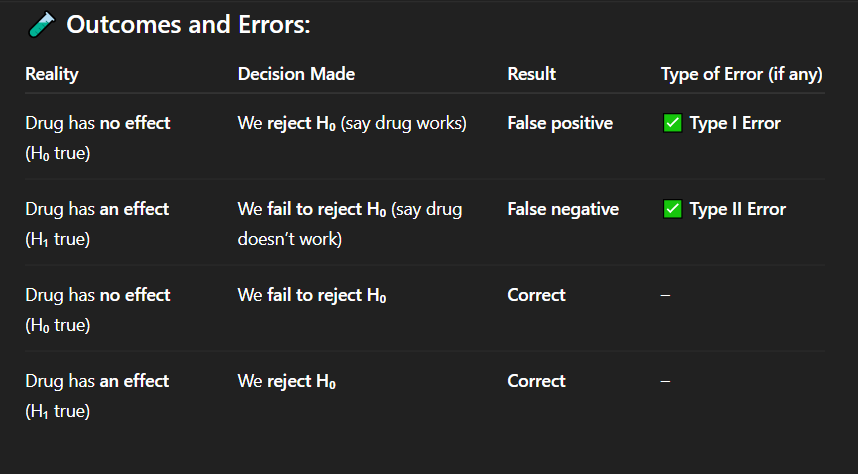
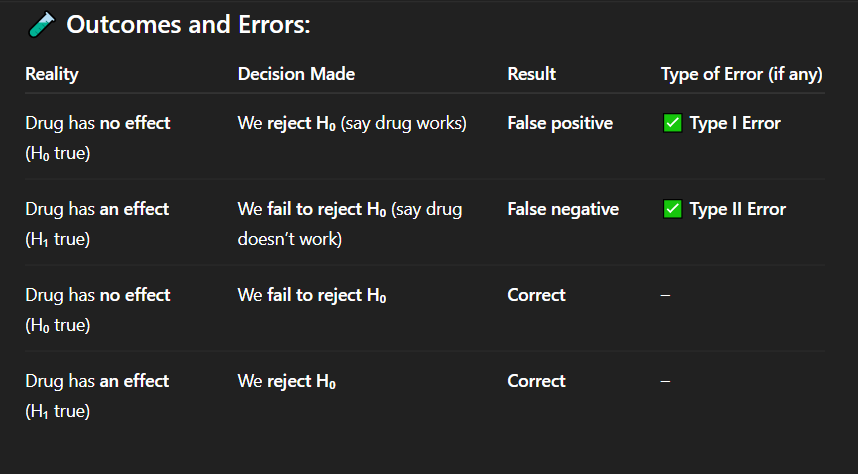
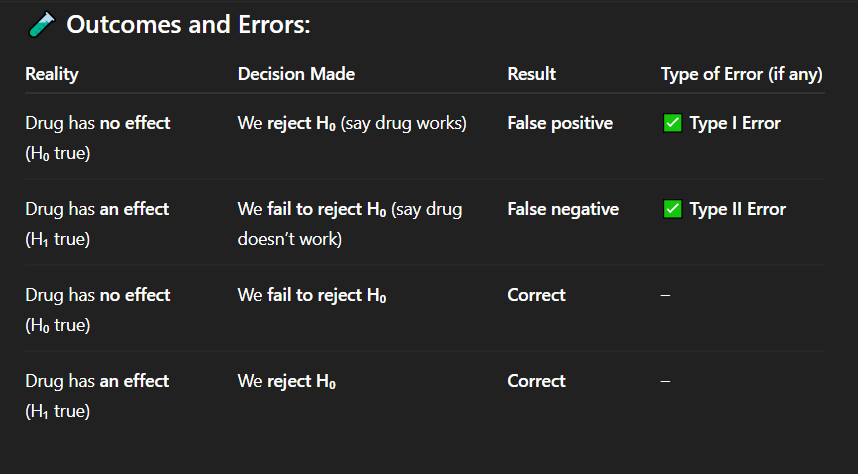
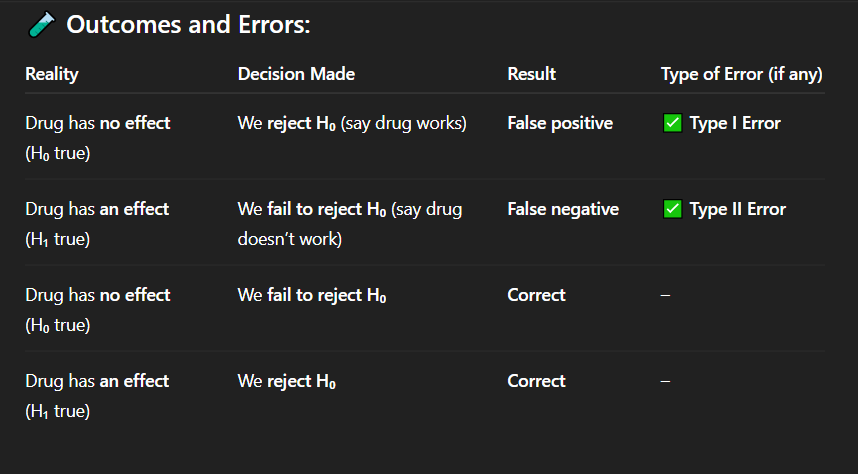
Correct Answer: A. Drug has no effect, but we say it works
Explanation: A false positive means detecting an effect when none exists — a Type I error.
In which of the following cases is there a false positive result?
A. Drug has no effect, but we say it works
B. Drug has an effect, but we fail to detect it
C. Drug has no effect, and we say it doesn't work
D. Drug has an effect, and we say it works
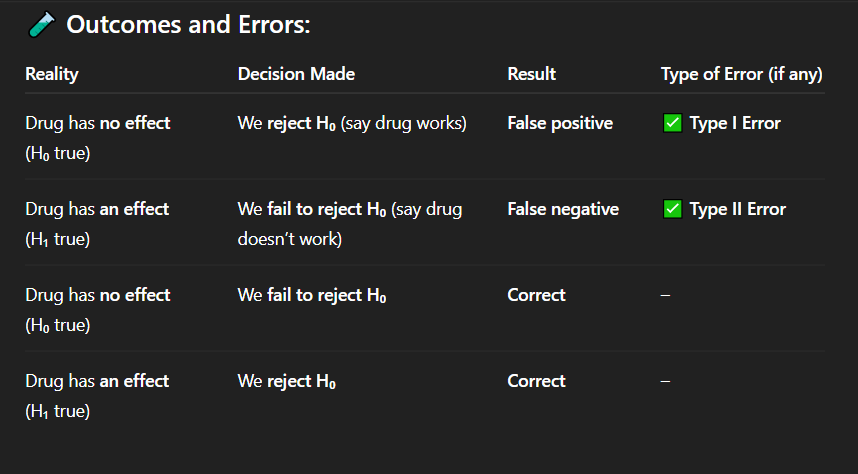
Correct Answer: C. Correct decision
Explanation: When the drug truly has no effect and we do not reject the null hypothesis, our conclusion is accurate — a correct decision.
If the drug has no effect and we fail to reject the null hypothesis, what is the result?
A. Type I error
B. Type II error
C. Correct decision
D. False negative
Correct Answer: A. Type I error (false positive)
Explanation: This is a Type I error — the researchers incorrectly rejected a true null hypothesis, falsely claiming the drug is effective.
A pharmaceutical company is testing a new drug. In reality, the drug has no effect on patients' blood pressure. However, based on statistical analysis, the researchers reject the null hypothesis and conclude that the drug works.
What type of error has been made in this scenario?
A. Type I error (false positive)
B. Type II error (false negative)
C. No error
D. Measurement error
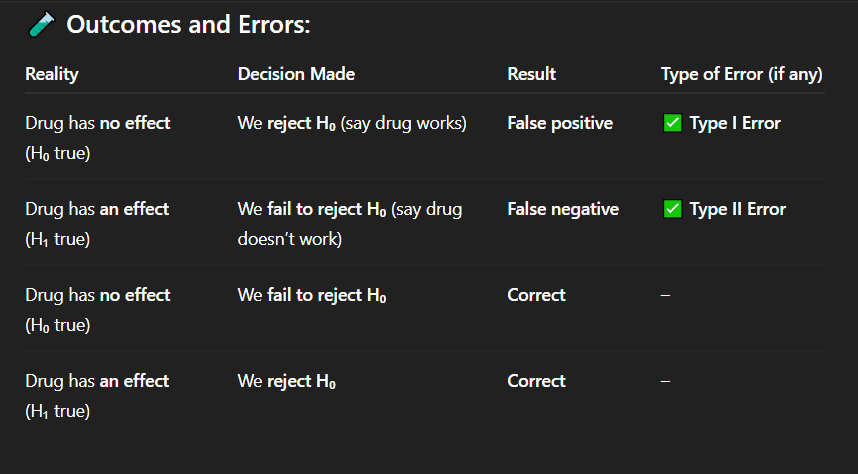
Correct Answer: B. Type II error
Explanation: This is a Type II error — a false negative. The drug works, but the researchers failed to detect its effect.
During a clinical trial, the drug being tested does reduce blood pressure in reality. However, the statistical test results lead researchers to fail to reject the null hypothesis, and they conclude the drug does not work.
Which type of error best describes this outcome?
A. Type I error
B. Type II error
C. Correct decision
D. Sampling error
Correct Answer: C. Correct decision
Explanation: This is a correct decision — the null hypothesis is true, and the researchers did not reject it.
A drug truly has no medical benefit, and researchers run a hypothesis test. The test result shows no statistically significant effect, so they do not reject the null hypothesis.
What is the classification of this decision?
A. Type I error
B. Type II error
C. Correct decision
D. Biased conclusion
Correct Answer: C. Correct rejection of H₀
Explanation: This is a correct decision — the alternative hypothesis is true, and the null hypothesis was appropriately rejected.
In a medical experiment, the researchers correctly identify that a new treatment has a real positive effect. The treatment does work, and they reject the null hypothesis.
Which of the following best describes this outcome?
A. Type I error
B. Type II error
C. Correct rejection of H₀
D. False negative
Correct Answer: B. Type I error; an ineffective drug may be given to patients
Explanation: This is a Type I error — concluding the drug is effective when it's not. The consequence could be widespread use of an ineffective treatment.
Imagine you are interpreting the results of a drug trial. The drug is ineffective in reality, but the analysis concludes it is effective, leading to approval for public use.
What error has occurred, and what could be the consequence?
A. Type II error; patients may miss out on a good treatment
B. Type I error; an ineffective drug may be given to patients
C. No error; the drug was properly tested
D. Type I error; a good drug was not approved