Random Variables

Random Variable

A variable whose numerical value is based on the outcome of a random event; denoted with a capital letter w/ a lowercase letter for the corresponding values

A random variable is “discrete” when..

we can list all of the outcomes, ifi we can’t then it’s “continuous”

Probability Model of a Random Variable

The collection of all possible values and probabilities that they occur

Expected Value (E(X)/𝝁)

The value calculated based on a probability model and LLN; the mean of a random variable

Expected Value Formula

𝝁= E(X) = ⅀(X(P(X))

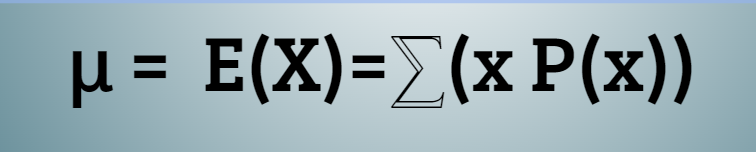
Variance

expected value of squared deviations of the values, found by multiplying each by the appropriate probability and sum those products

Standard Deviation

Square root of the variance

Variance Formula

𝝈² = Var(X) =⅀(x-μ)² P(x)

Standard Deviation Formula

  𝝈= SD(X) =√⅀(x-μ)² P(x)

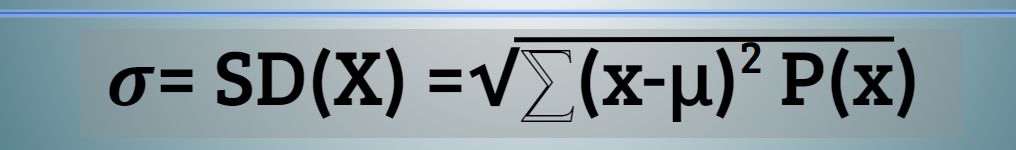
Formulas for adding a constant to the Mean and Variance

E(X±c)= E(x)±c  

Variance: Var(X±c)= Var(X)

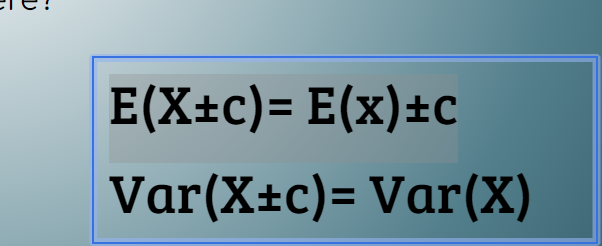
Adding a Constant..

Shifts the mean up by that constant but doesn’t change the spread

Rescaling (multiplying by a constant)..

Multiplies both the mean and spread by that constant

Formulas of Mean and Variance for Rescaling

Mean: E(aX)=aE(x)

Var(aX)=a² Var(X) [b/c SD is square root of variance]

The mean of the sum/ difference of 2 random variables is the sum/difference of the means formula

E(X±Y)= E(X)±E(Y)

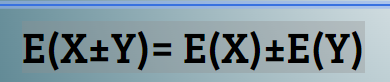
Pythagorean Theorem of Statistics

We always add variances because the variability in the differences increases just as much as the variability in the sums (If the random variables are independent, the variance of their sum OR difference is always the sum of the variances)

Pythagorean CTheorem of Statistics Formula

Var(X±Y)= Var(X)+Var(Y)

Continuous Random Variable

can take on any value, but not every value will have a probability; everything that applies to discrete random variables is also applicable for them too

For a normal random variable..

The probability that it falls within an interval is just the area under the normal curve over that interval

Regardless of shape (Normal, skewed, uniform, or bimodal) all continuous random variables have..

means (expected values) and variances

When 2 INDEPENDENT continuous random variables have Normal models.

So does their sum or differences (allows us to apply Normal Model probabilities to random variables)

What can go wrong?

• Make sure that probability models and using normal distribution is reasonable

• Watch out for variables that arent independent

• Always add variances even when looking for differences

• Write random variables separately