Pre-Calc: Exam Ch. 1-7.2 Cumulative: Ch 2-6

Parent Graphs: Identity

f(x)=x (Linear: y=mx+b, where m is the slope and b is the y-int.)

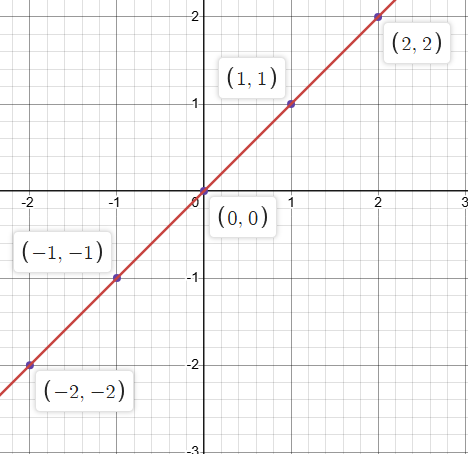
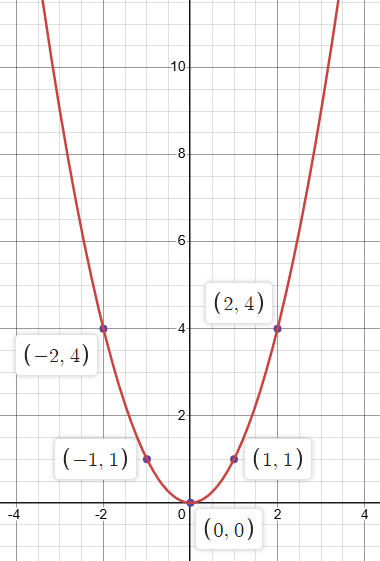
Parent Graphs: Quadratic

f(x)=x²

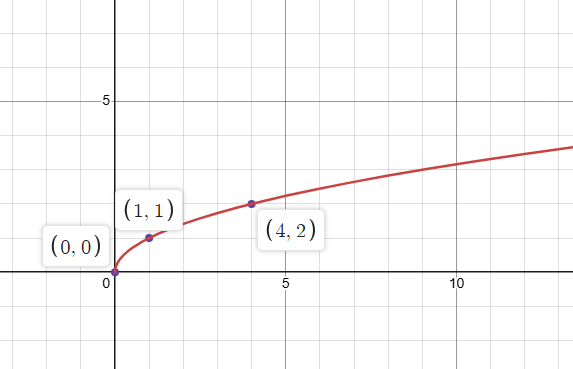
Parent Graphs: Square Root

f(x)=\sqrt{x}

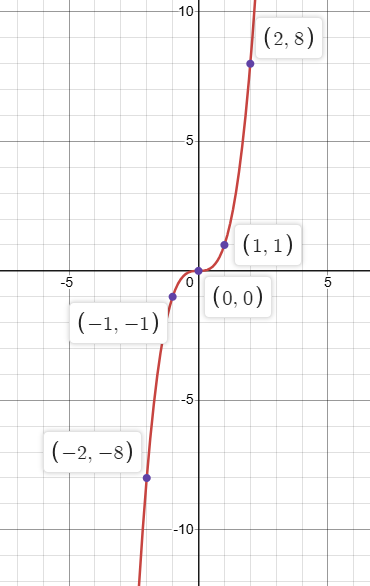
Parent Graphs: Cubic

f(x)=x³

Parent Graphs: Cube Root

f(x)=\sqrt[3]{x}

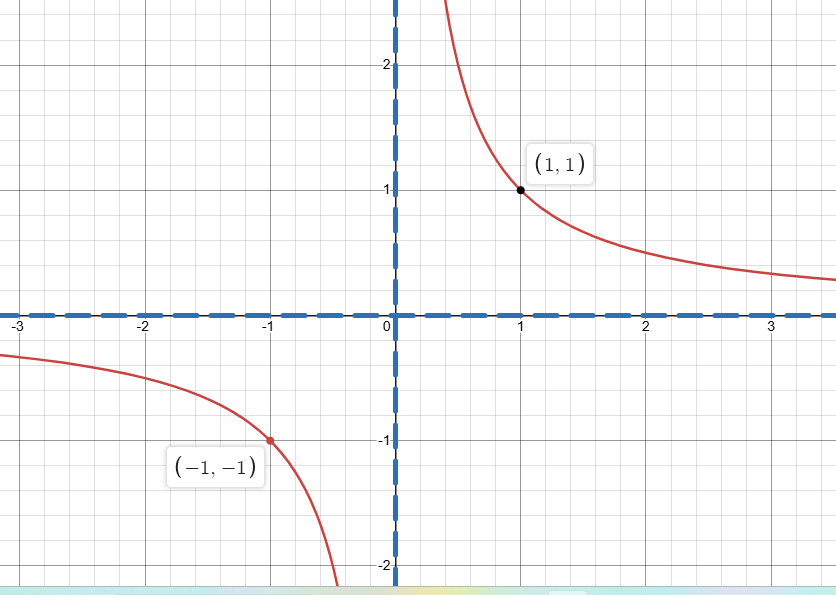
Parent Graphs: Reciprocal

f(x)=1/x, with asymptotes at x=0 and y=0

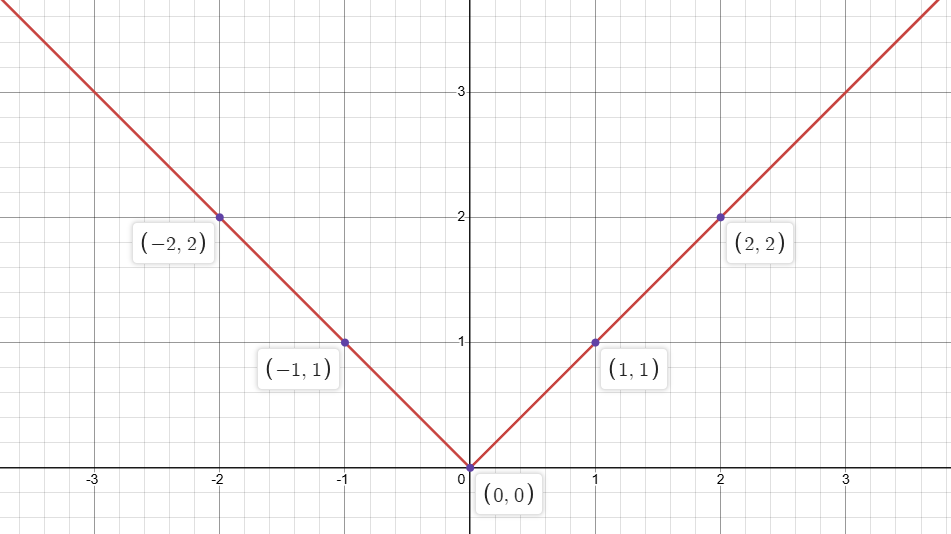
Parent Graphs: Absolute Value

f(x)=\left\vert x\right\vert

Transformations: Vertical (Outside)

f(x)+n: Shifts up.

f(x)-n: Shifts down.

(n)f(x): Stretches the graph.

f(x)/n: Compresses the graph.

-f(x): Reflects over the x-axis.

Transformations: Horizontal (Inside)

f(x-n): Shifts right.

f(x+n): Shifts left.

f(x(n)): Compresses the graph.

f(x/n): Stretches the graph.

f(-x): Reflects over the y-axis.

Even Functions

Functions with an even exponent (i.e. x²) that are the same when flipped over the y-axis, or f(x)=f(-x)

Odd Functions

Functions with an odd exponent (i.e. x³) that are the same when flipped over the y- and x-axes, or f(x)=-f(-x)

To find if a graph has symmetry around the y-axis, origin, or both…

Solve f(x), f(-x), and -f(-x), letting x=1.

If f(x)=f(-x), f(x)=-f(-x), or both, the function has symmetry over the y-axis/origin/both.

If neither, the function has no symmetry.

Operations with Functions

Addition: f(x)+g(x)=(f+g)(x)

Subtraction: f(x)-g(x)=(f-g)(x)

Multiplication: f(x)(g(x))=(fg)(x)

Division: f(x)/g(x)=(f/g)(x)

Function Composition

f(g(x))=(f o g)(x), or make the output of g(x) the input of f(x), and vice versa.

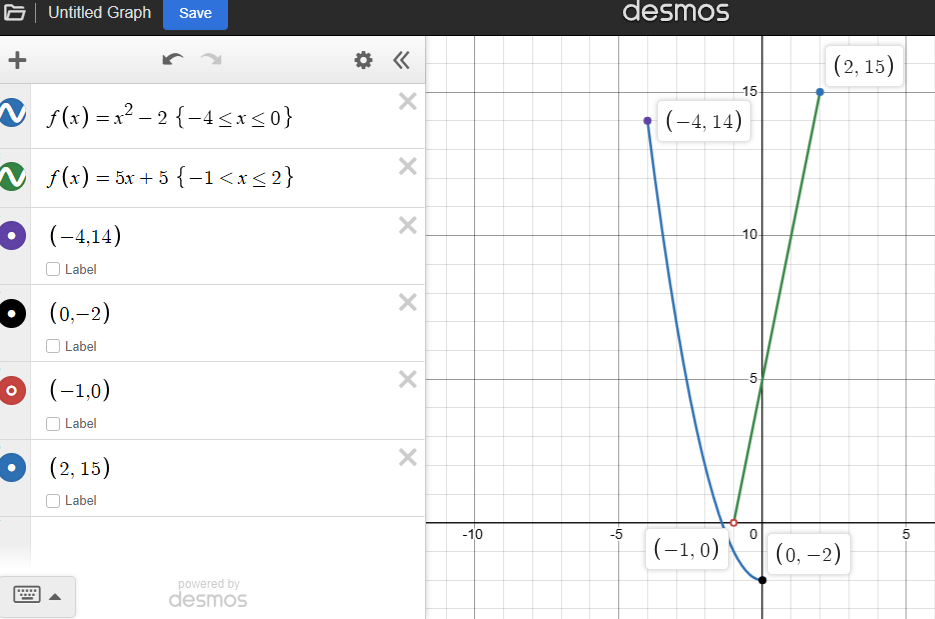
Piecewise Functions

Functions broken up into different parts, with each part having a restriction on it’s domain.

To graph piecewise functions…

1) Make the restrictions of the given function’s domain (i.e 3<x<1) the inputs of the given function.

2) Solve for f(x) and plot the given points, making sure that less/greater than signs are closed and less/greater than or equal to signs are open.

3) Repeat the process until all of the functions are graphed.

*For f(x)=n functions, go across the given domain (i.e x>-4 is the open point (-4,n)).

Difference Quotient

\frac{f(x+h)-f(x)}{h}

…where x+h is an input for f(x)

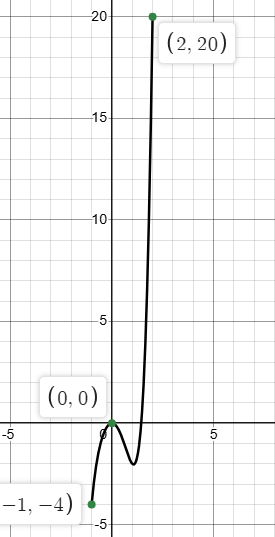
Intervals

The x-values over which a graph can increase or decrease.

In this graph, it increases over the interval (-1,0) and decreases over the interval (2,n).

To solve absolute value equations…

1*) Make sure that any values near the absolute value symbol are moved to the right side of the equation.

2) Solve for two instances, one where the right side is positive and one where the right side is negative. If there are absolute value signs on both sides, ignore the ones on the right.

*If there is a negative number on the right side, there is no solution to the equation.

To solve absolute value inequalities…

1) Determine the type of inequality ([] represent absolute value signs):

GreatOR: [A]>B—>A>B or A<-B

Less thAND: [A]<B—>-B<A<B

2) Solve the inequalities.

3) Use the values given to plug in test values into the original equation in order to find the solution set.

</= or >/= signs are closed dots and use brackets.

< or > signs are open dots and use parentheses.

Complex Numbers

Numbers in the form a+bi, where a is the real part and b is the imaginary part.

Operations with Complex Numbers:

Addition/Subtraction: Combine like terms.

Multiplication: Use FOIL (First, Outer, Inner, Last).

Division: Divide by the complex conjugate, a-bi, of the denominator.

Quadratic: Standard Form

y=ax²+bx+c

Quadratic Formula

x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}

Quadratic: Vertex Form

y=a(x-h)^2+k

…where the A.O.S is x=h, and the vertex is (h,k)

Standard to Vertex Form: Method 1:

1) Find the A.O.S using x=-b/2a. This gives an x-value.

2) Use the x-value to solve for y.

3) Plug in the x- and y-values into the vertex form equation.

4*) Find the x-intercepts by factoring the original equation.

5*) Find the y-intercepts by solving for f(0).

Standard to Quadratic Form: Method 2 (Completing the Square):

1) Move the constant to the left side of the equation. Factor out the right if necessary.

2) Take half of the coefficient x and square it. Apply the new value to the left with the opposite sign.

3) Convert the right side to a perfect square, (x-c)² and move the constant back to the right side.

4*) Use the original equation to find the x-intercepts.

5*) Use the new equation to find the y-intercept by solving for f(0).

To solve a quadratic by completing the square…

1) Move the constant to the right side.

2*) Make sure that the coefficient of x² is 1 by dividing both sides by the coefficient.

3) Take half of the coefficient of x and square it, and put the new value on both sides.

4) Clean up the right side and convert the left to a perfect square binomial, (x-c)².

5) Solve the remaining equation.

To solve a quadratic inequality…

1) Factor the equation, and find x by setting each factor equal to 0.

2) Use the factors in order to find the solution set by plugging in test values.

Note that < or > signs are marked with parentheses and </= or >/= signs are marked with brackets.

To solve a system of equations involving a quadratic…

1) If provided, use substitution to plug in the quadratic equation into the other equation.

2) Solve the new equation and factor.

3) Solve for y with both of the new roots. Note that in the solution set, the lesser x- and y-values come first.

Circle Formula: Standard Form

(x-h)²+(y-k)²=r

…where (h,k) is the center of the circle an r is the radius (how far each point is to the center)

To convert from conic (non-standard) to standard form…

1) Move the constant to the right, and group the x- and y-values.

2) Take half of the coefficients of x and y and square them.

3) Clean up the right side and convert the x and y trinomials into perfect square binomials, (x-c)^2.

End Behavior (a is POSITIVE)

For functions with an odd degree (i.e. 3):

As x—> \infty f(x)—>\infty

As x—>-\infty f(x)—>-\infty

For functions with an even degree (i.e. 2):

As x—>\infty f(x)—> \infty

As x—> -\infty f(x)—> \infty

End Behavior (a is NEGATIVE)

For functions with an odd degree (i.e. 3):

As x—> \infty f(x)—>-\infty

As x—>-\infty f(x)—>\infty

For functions with an even degree (i.e. 2):

As x—>\infty f(x)—> -\infty

As x—> -\infty f(x)—> -\infty

Multiplicities

The number of times a factor/zero/root is listed. This affects the graph of the polynomial:

Odd multiplicities cross the x-axis at a given zero.

Even multiplicities don’t cross the x-axis, rather they touch the zero and bounce back in the direction of the graph.

To sketch the graph of a polynomial…

1) Solve for the zeros and their multiplicities. Recall that odd multiplicities cross the x-axis at a given zero and even multiplicities don’t cross, but bounce in the direction of the graph at a given zero.

2) Know the end behavior of the graph. Odd functions have arrows pointing in opposite directions, and even functions have arrows pointing in the same direction.

3) Find the y-intercept by solving for f(0) and find any other points on the graph.

To perform synthetic division of polynomials…

1) If necessary, find the rational zeros by solving p/q, where p is the factors of the constant term and q is the factors of the leading coefficient.

2) Plug in any zero and list all the terms of the polynomial, adding 0 for any missing terms.

3) Bring the first number down, and multiply it by the zero.

4) Add the new number to the next number, then multiply the resulting number by the zero.

5) Repeat Step 4 until no numbers are left.

6) Write your answer with one less degree than the original polynomial, and put the remainder over the divisor like so:

(i.e 2x^4-x^3+7x^2+10x-7+55/x-4)

To find the zeros and multiplicities of polynomials…

1) Find the rational zeros by solving p/q, where p is the factors of the constant term and q is the factors of the leading coefficient.

2) Perform synthetic division by testing each root until one root gives a remainder of 0.

3) Factor the resulting polynomial by grouping if possible.

4) Solve for the zeroes by setting each factor equal to 0.

Conjugate Zeros Theorem

If f(x) is a polynomial with real coefficients, and a+bi (b is NOT equal to 0) is a zero of f(x), then its conjugate a-bi is also a zero of f(x).

Intermediate Value Theorem

Let f be polynomial function. For a<b, if f(a) and f(b) have opposite signs, then f has at least one zero on the interval [a,b].

To prove the theorem, solve for f(a) and f(b) to check if they have opposite signs.

The function must also cross through the zero, and it MUST be continuous.

Rational (Reciprocal) Functions

Two functions divided by one another: \frac{f\left(x\right)}{g\left(x\right)},g(x)\ne0

They are not continuous due to having asymptotes, but not all rational functions have them.

To find the x- and y- intercepts of a rational function…

x-intercepts:

1) If possible/necessary, factor the numerator and denominator.

2) Set the numerator of the function equal to 0.

3) Set each factor equal to 0, and eliminate any factors that would result in division by 0.

4) Write in the form (x,0).

y-intercepts:

1) Solve for f(0).

2) Write in the form (0, f(x)). There is no y-intercept if f(0) involves division by zero.

To find the vertical asymptotes of a rational function…

1) Factor the denominator, if possible/necessary.

2) Set each factor equal to 0. The zeros given tell where the denominator will equal 0.

To find the horizontal asymptotes of a rational function…

Look at the powers on the numerator and denominator:

If the numerator power < denominator power, there is a horizontal asymptote at y=0.

If the numerator power = denominator power, there is a horizontal asymptote at a/b, where a and b are leading coefficients.

If the numerator power > denominator power, there is no horizontal asymptotes, but there is a slant/quadratic asymptote.

To graph a rational function…

1) Factor the numerator and denominator.

Factored form:

2a) Find the x-intercepts by setting the numerator equal to 0.

2b) Eliminate any zeroes that result in division by 0.

3) Find the vertical asymptotes by setting each factor in the denominator equal to 0.

4) Find any holes (repeated factor) in the graph.

5) Find any other points by plugging in other values.

Original form:

6) Find the horizontal asymptotes by comparing powers.

7) Find the y-intercept by solving for f(0).

To solve a rational equation…

1) Find the LCM of the denominators.

2) Multiply both sides by the LCM.

3) Solve anything remaining, and check for extraneous solutions (division by 0).

To solve a rational inequatity…

1) Make sure the equation is in the form \frac{f(x)}{g(x)}<\colon>\colon\le\colon\ge0 .

2) Solve f(x) and g(x) by setting each factor equal to 0.

3) Plot the values and plug in test solutions, but keep in mind that while the numerator can be an open or closed interval, the denominator must ALWAYS be an open interval.

Radical (Power/Root) Function Formula

f(x)=a\sqrt{b(x-h)}+k

…where the index is the number outside the root that dictates the graph, h shifts left or right (sign changes), k shifts up or down, a vertically stretches (greater than 1) or compresses (less than 1), b horizontally stretches (less than 1) or compresses (greater than 1), -a reflects over the y-axis, and -b reflects over the x-axis.

To find the zeros of a radical function…

1) Set the equation equal to 0 and solve.

2) Isolate the root, then square both sides.

3) Solve the remaining sides and check if f(x)=0.

To solve radical equations…

One root/Two isolated roots on both sides/Indexes greater than 2:

1) Isolate the root, then square both sides.

2) Solve and check for extraneous solutions.

Two roots, but only one is isolated:

1) Isolate one root on one side (if necessary), then square both sides.

2) FOIL (First, Outer, Inner, Last) the remaining side.

3) Clean up in order to isolate the second square root, then square both sides again.

4) Solve anything remaining, then check for extraneous solutions.

Horizontal Line Test

Used to determine whether or not a function is one-to-one.

If a horizontal line crosses any point of the graph at exactly one point, then the function is one-to-one.

If a horizontal line crosses any point of the graph at more than one point, then the function is NOT one-to-one.

To find the inverse function…

1) Replace f(x) with y.

1) Swap the x and y.

2) Solve for y.

3) Rewrite y as f^-1(x).

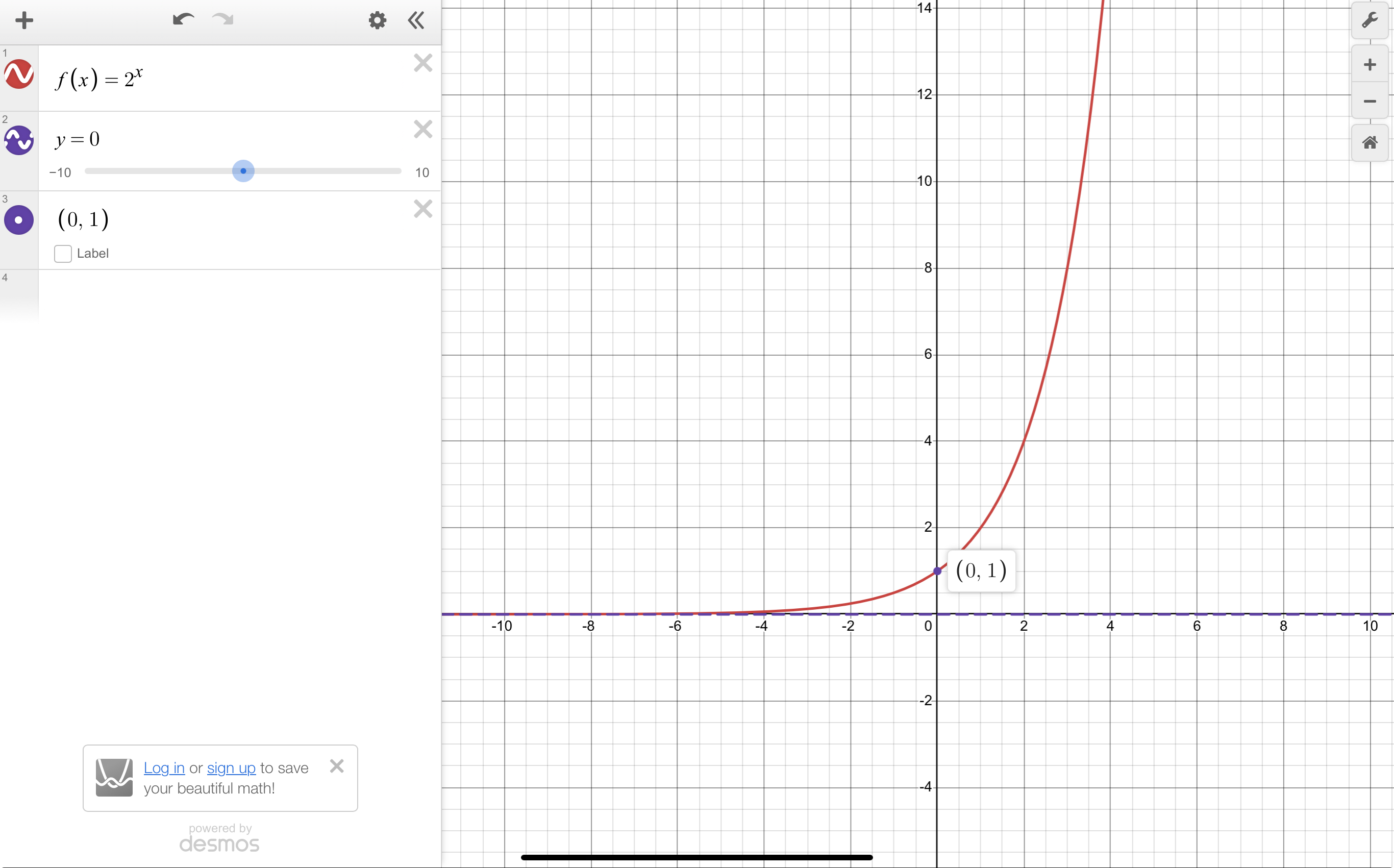
Exponential Function Graphs

i.e. f(x)=2^{x}

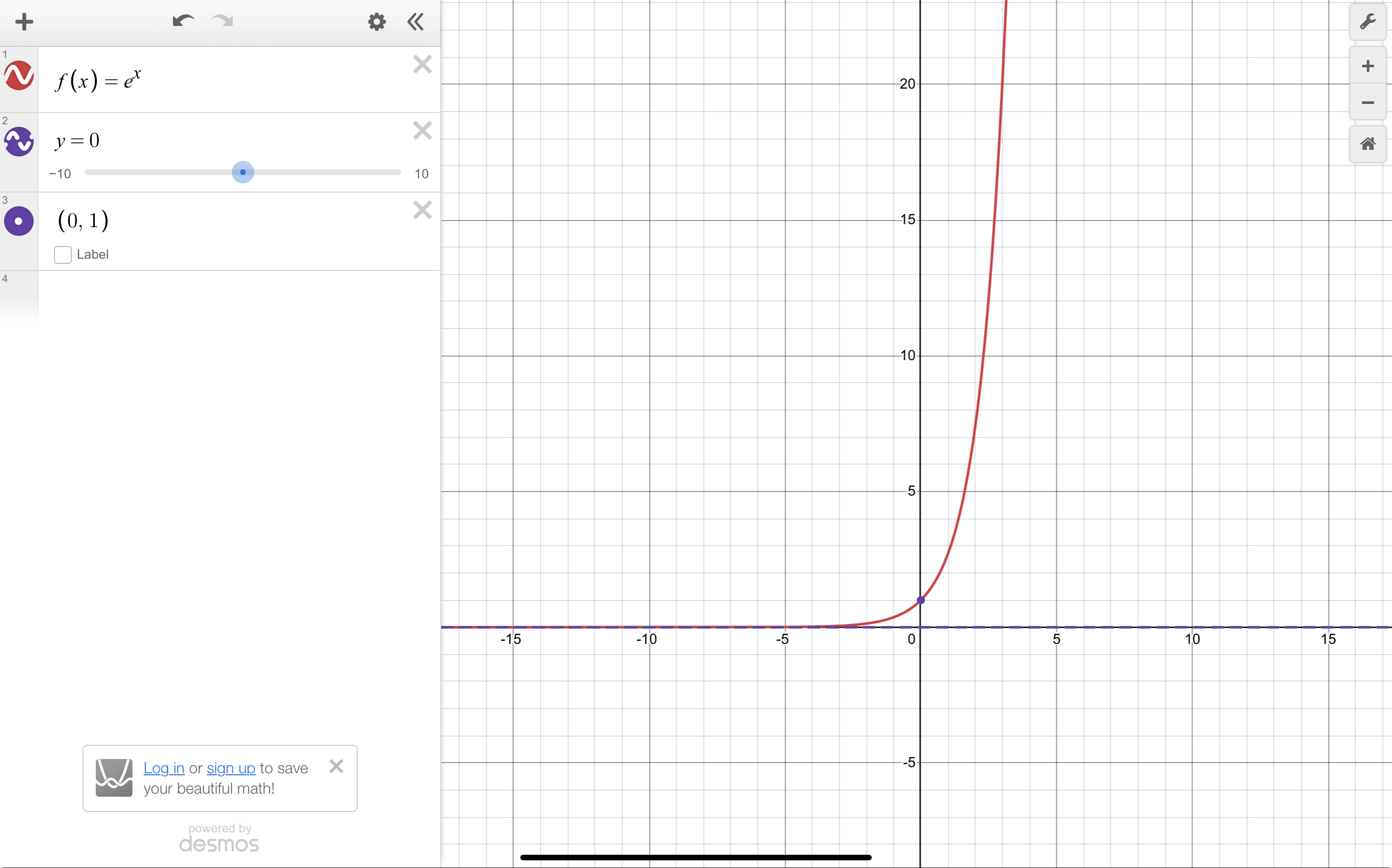
Parent Graphs: Base e

f(x)=e^x

To solve exponential equations…That can be rewritten with matching bases

1) Rewrite any side of the equation to a smaller base until the bases match.

2) Distribute, if necessary.

3) Drop the bases and solve the remaining equation.

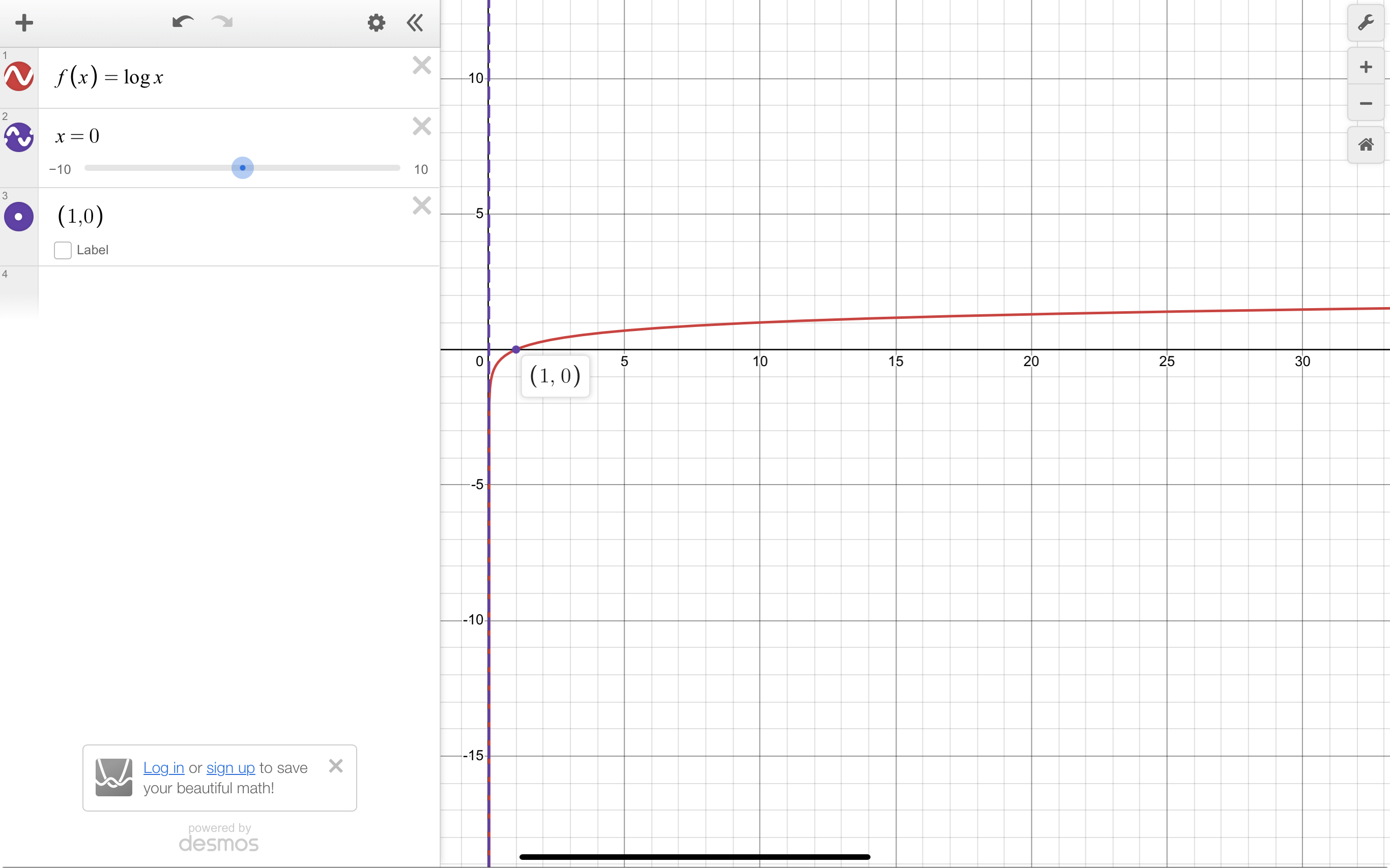
Parent Graphs: Logarithmic

f(x)=log x

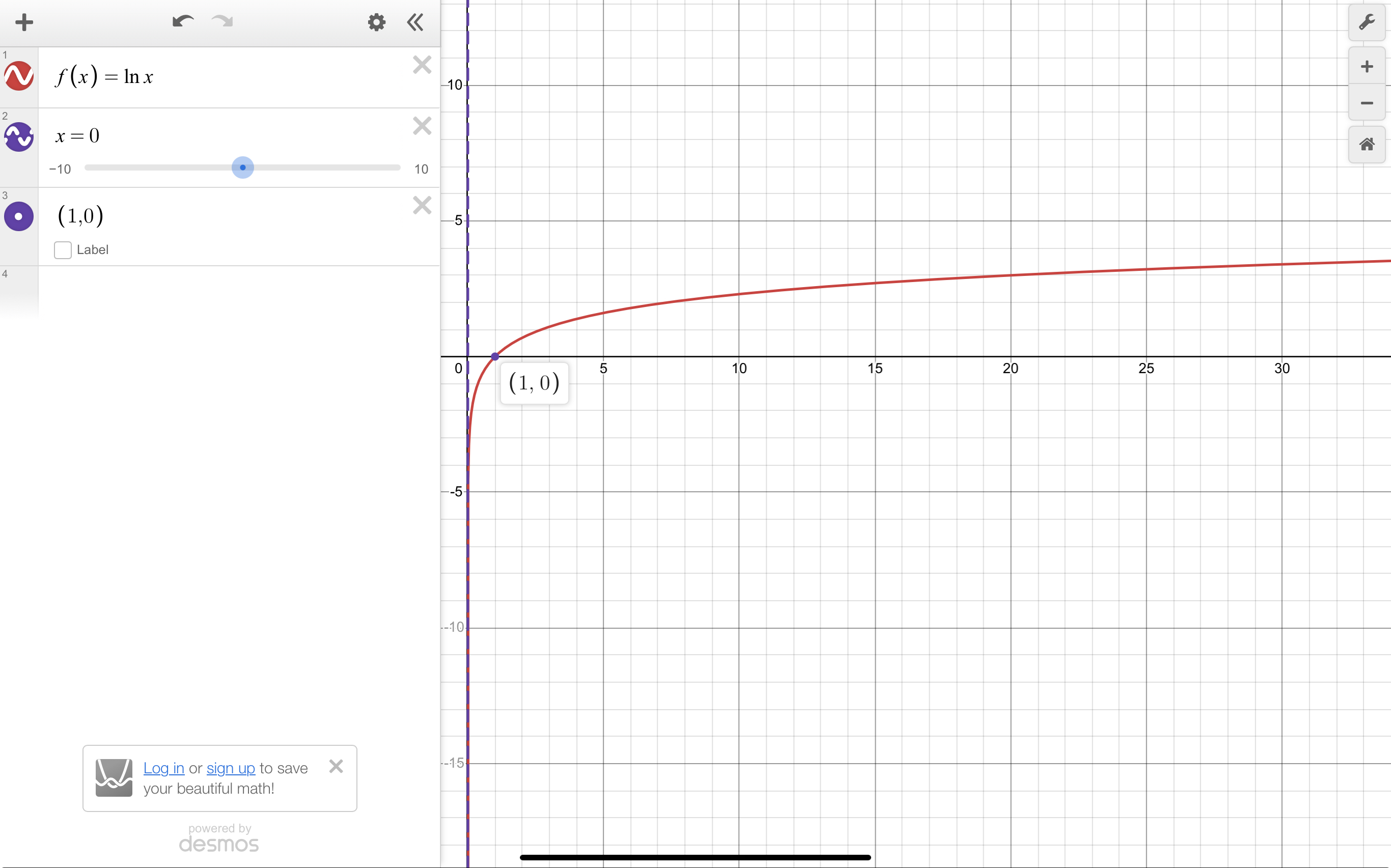
Parent Graphs: Natural Logarithm

f(x)=ln x (\log_{e}x)

Logarithm/Exponent Relationship

\log_{b}y=x ←→b^{y}=x

To simplify a logarithmic expression…

1) Rewrite the logarithmic expression in exponential form.

2) Make a guess as to what power y will make the equation equal x.

i.e. \log_416 =?

4^{?}=16

4^2=16

The answer is 2.

Basic Properties of Logarithms

1) \log_{b}1=0

2) \log_{b}b=1

3) \log_{b}b^{x}=x

4) b^{\log_{b}x}=x

Rules of Logarithms

Product Rule: \log_{b}DE=\log_{b}D+\log_{b}E

Quotient Rule: \log_{b}\frac{D}{E}=\log_{b}D-\log_{b}E

Power Rule: \log_{b}F^{G}=G\log_{b}F

To solve exponential equations without matching bases…

One isolated exponent:

1) Take the log or ln of both sides.

2) Move the exponent down.

3) Solve the remaining equation.

One exponent that is not isolated:

1) Isolate the exponent.

2) Take the log (or ln, if applicable) of both sides.

3) Move the exponent down (and cancel out the ln e)

4) Solve. Make sure to put the fraction (if any) to the left of the log/ln.

Two isolated exponents:

1) Take the log of both sides.

2) Move the exponents down.

3) If possible, split the logarithm on the left/right into two logarithms.

4) Move all logarithms with a variable to one side.

5) Factor out the variable and solve.

To solve an equation with one logarithm on one side…

1) Convert to exponential form.

2) Cross-multiply and solve the remaining equation.

3*) Check for extraneous solutions.

To solve an equation with logarithms on both sides…

1) Cancel out the logarithms.

2) Solve the remaining equation.

3) Check for extraneous solutions.

To solve an equation with two logs on one side and one on the other…

1) Condense the two logarithms into a single logarithm via the product or quotient rule.

2*) If necessary, move any exponents down.

3) Cancel out the remaining logarithms.

4) Solve the remaining equation.

5) Check for extraneous solutions.