Ch9 Artificial Neural Networks

what are artificial neural networks

a collection of connected comutational units (neurons), arranged in interconnected layers

very popular for supervised and unsupervised learning

state of the art across many comlex domeins, mainly based on unstructured data

what do we mean when we say that Artificial neural networks are very powerful and flexible ?

• more layers / neurons → more capacity / complexity

• specialized architectures

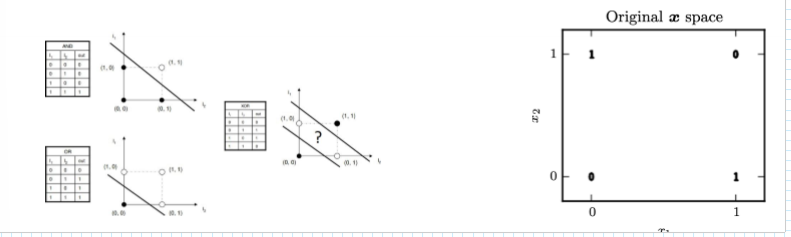
XOR problem

a function that a perceptron cannot learn

exclusive or is a logical operation that is true if and only if its arguments differ

the perceptron

an algorithm for supervised learning of binary classifiers

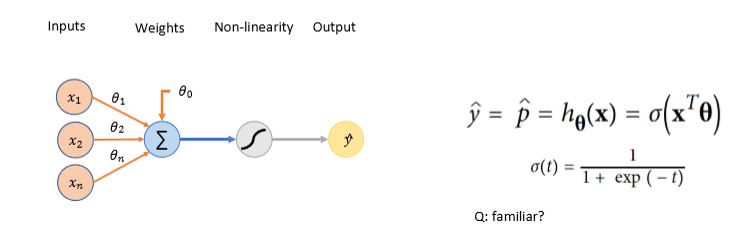
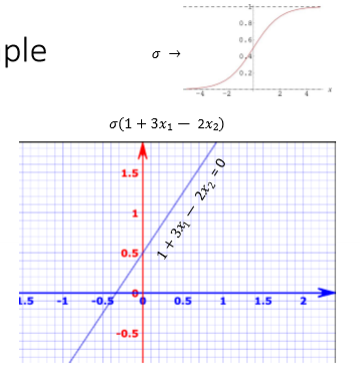
what do we mean when we say that a perceptron with a (sigmoid) activation function can only model linear decision boudaries

the result of the perceptron will be a sigmoid function, but the classification that happens is stil a linear classification since the decison boundary is still linear

→ the function that goes through the activation function is still linear

what is the solution to the XOR problem

a non linear activation function in the hidden layer

• input layer : raw features, no computation thus no activation function

• in hidden layer : non linear activation function required to model complex non linear patterns (often ReLU)

• in outpuut layer : classification (usually sigmoid), regression → usually none (linear)

notation X

is a matrix containing all the feature values (excluding labels) of all instances (m) in the dataset. There is one row per instance and the ith row is equal to the transoise if x(i)

multi-layerd perceptron also called

feedforward (fully connected) artificial neural network ANN

ANN recap : input layer

no computation, input data, #nodes = #features

ANN recap hidden layers

intermediate layers, everything in between input and output layers

ANN : recap : output layer

layers producing the final result

universal approximation theorem

a neural network with 1 hidden layer can represent any continuous function (under mild constraints and given enough width)

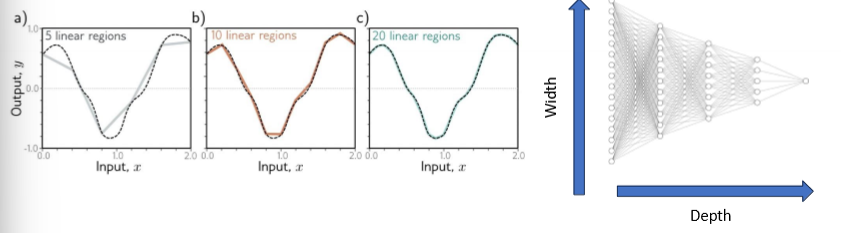
if we know the universal approximation theorem, why do we use more than 1 hidden layer ?

why deep and not wide learning

deep learning is

• faster and easier to train

• generalizes better (intuition : representation perspective)

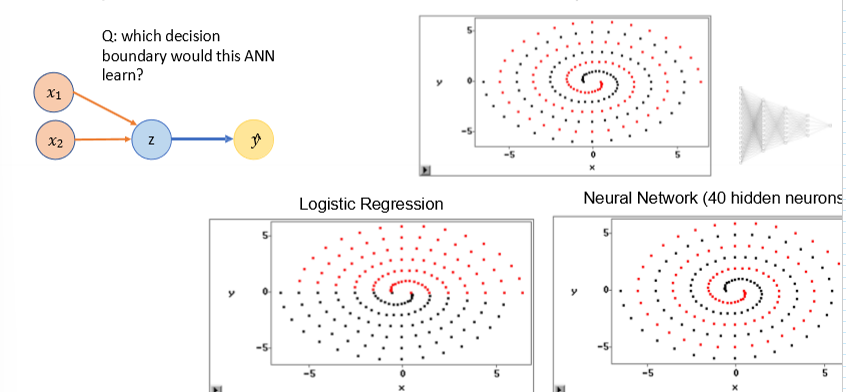
Q : which decision boundary would this ANN learn

Logistic regression bc we only have one node with a logistic regression

what is training

updating the (trainable) parameters of the network to minimize the loss

which are the common loss functions that are used

regression : MSE

classification - cross entropy

gradient

a vector that describes the rate of change of a function

components of the vector are the partial derivatives of the loss with respect to the network parameters

points in the direction of greatest incease of a function

is zero at a local maximum or local minimum

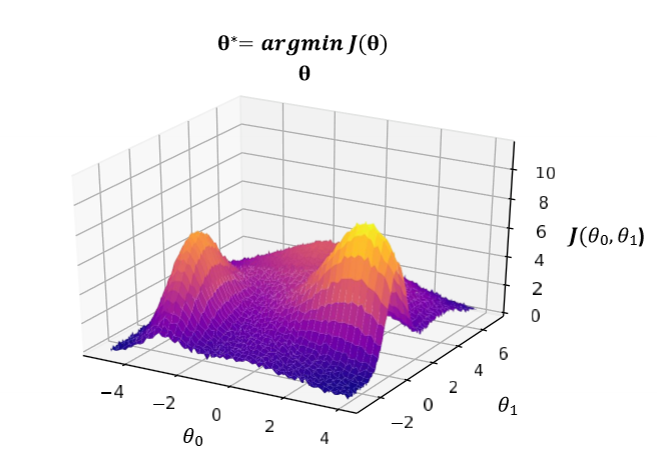
how does loss optimization work

gradient descent

• randomly pick (theta1 and 2)

• compute gradient (partial derivative of the loss function)

• take step in the opposite direction (with n learning rate)

• repeat until convergence

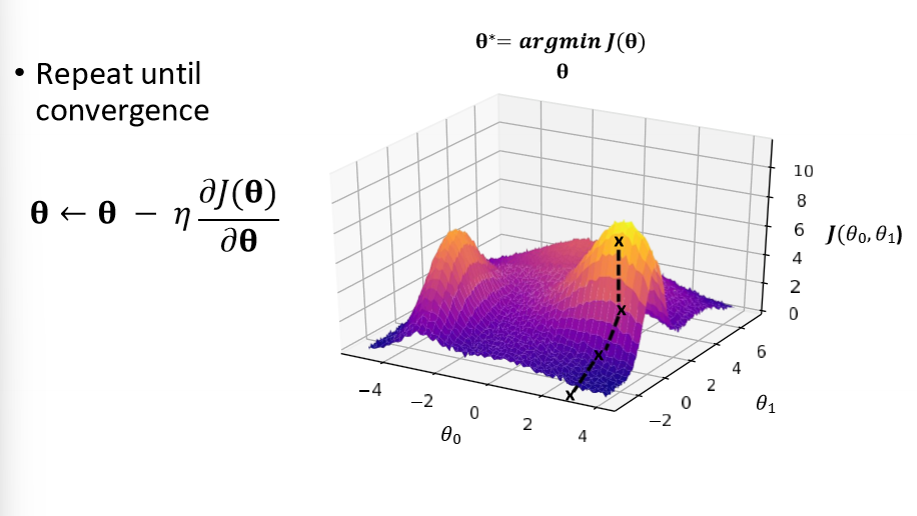
gradient descent, an algorithm

1) initialize weights randomly N(0, sigma²)

2) loop until convergence

• 3) compute partial derivative

• 4) update according to theta = theta - learning rate* partial derivative

5) return weights

what happens due to non-linearities :

non-convex optimization problem

optimisation gets stucj in a suboptimal point (parameter value)

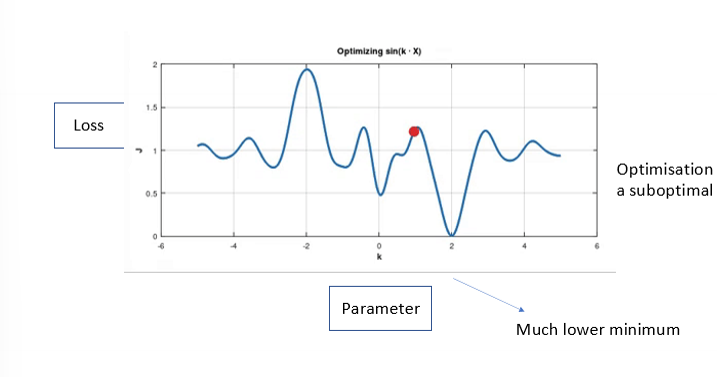
gradient descent : solution to local minima

increase the learning rate

stochastic gradient descent (use mini batches)

gradient descent : solution to local minima : stochastic gradient descent

use minu-batches

• calculate each update on a mini-batch → subset of full training set

• since we calculate the loss for each subset, it will not be exactly the same

shuffle the observations in the training set, run through the whole training set in mini batches (1 epoc) then we shuffle again and we do the same thing

local minima in gradient descent is less a problem than it used to be,

with modern activations

and high dimensionallity → with more dimensions you can escape more easely the local minima

how to use gradient descent for huge networks

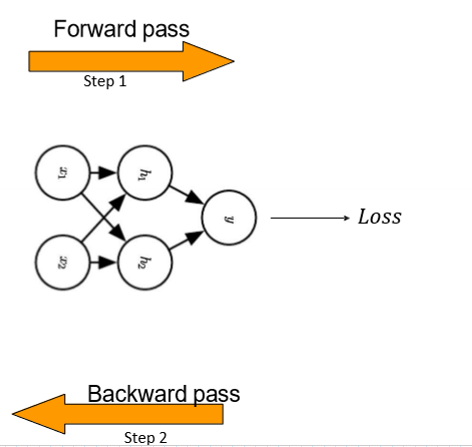
backpropagation : is a highly efficient method to compute the gradients (in neural network).

computed gradients can then be used for gradient descent to update parameters

backpropagation : GD

1) for each input in the batch, compute the network’s output

2) propagate the error term backwards to the preceding layers

batch gradient descent

update the weights (with GD) using the entire training set for each update

mini-batch gradient descent

update the weights using a subsample from the training set

1 epoch = 1 run of all training observations through the network

what happens when the learning rate is too high

oscillations, algorithm will diverge

what happens when the learning rate is too small

slow progress

if the training set = 10.000, validation set = 1.000, and mini-batch size = 100

how many epochs after 1.000 mini-batches ?

10 epochs

if you use the full dataset for each update, how are updates and epochs related

then the number of epochs = the number of updates

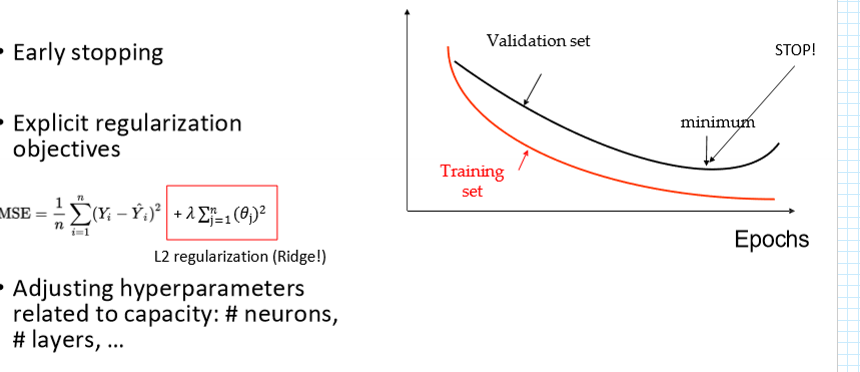
how can we avoid overfitting when training Gradient descent

• → they are prone to overfit

• early stopping

• esplicit regulkarization objectives

• adjusting hyperparameters related to capacity, #neurons, layers

hyperparameters KNN

• weigght initialization, activation function, loss, #layers, #neurons, early stopping rule, optimizer, explicit regularization terms

• → always use the validation set

• focus on those for which the loss is sensitive

what type of preprocessing needs to happen ANN

categorical data

• onehot encode

continuous data :

• standardize/ normalize

what do you need to learn non linear patterns

you need non-linear activations / feature transformations

what do the hidden layers learn so that the data is linearly separable

a representation

pros neural networks

• reduces the need for feature engineering

• can fit any function (non-linear or otherwise)

• extreme flexibility

• state of the art performance across many domains

feature engineering

the crucial process of transforming raw data into meaningful input variables (features) that machine learning models can use to learn patterns and make accurate predictions

cons to neural networks

• ‘ black box’, bad interpretability

• optimization is stochastic, solution possibly unstable

what can neural networks learn without requiring feature engineering

interaction effects and non-linear relationships