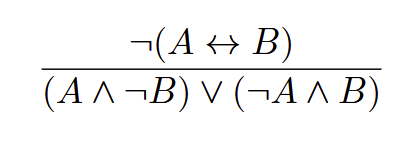1dm3

Tautology

A statement that is always true

Contradiction

A statement that is always false

De Morgan's Law

~(P ^ Q) = ~P v ~Q

~(P v Q) = ~P ^ ~Q

Idempotent Laws

P ^ P = P

P v P = P

Distributive Laws

P ^ (Q v R) = (P ^ Q) v (P ^ R)

P v (Q ^ R) = (P v Q) ^ (P v R)

Identity Laws

P ^ t = P

P v C = P

Absorption Laws

P v (P ^ Q) = P

P ^ (P v Q) = P

Sufficient condition

"R is sufficient condition for s" means "if r, then s"

If P, then Q

P is sufficient for Q

Necessary condition

"R is necessary for s" means "if not r, then not s"

If not P, then not Q

P is necessary for Q

If Q, then P

necessary condition

If not q, then not p

Contrapositive of "if p, then q"

Not p and not q

Conditional statement ("if p, then q") expressed as or

Modus tollens

If P, then Q.

Not Q.

Therefore, not P.

Modus ponens (primero)

If P, then Q.

P.

Therefore, Q.

Converse error (affirming the consequent)

If P, then Q.

Q.

Therefore, P.

Inverse error (denying the antecedent)

If P, then Q.

Not P.

Therefore, not Q.

NAND-gate

An "and" gate followed by a "not" gate. (sheffer stroke)

NOR-gate

An "or" gate followed by a "not" gate. (pierce arrow)

Recognizer

A circuit that outputs a 1 for only one combination of input signals

Two's complement

A way to represent the negative of a binary number.

2^n - a

Form of the two's complement

Proposition (statement)

A sentence that can either be true or false

Predicate

A sentence whose truth value cannot be determined because there is a variable or missing information

Vacuously true

If p is false, then q is true. This statement is True.

If p is false, then q is false. This statement is True.

Every time p is false, the statement is True! What is this called?

For all x, if P(x) then Q(x).

P(a) is true for a particular a.

Therefore, Q(a) is true for that particular a.

Universal modus ponens

For all x, if P(x) then Q(x).

Q(a) is false for a particular a.

Therefore, P(a) is false for that particular a.

Universal modus tollens

For all x, if P(x) then Q(x).

For all x, if Q(x) then R(x).

Therefore, for all x, if P(x) then R(x).

Universal transivity

Constructive proof of evidence

Showing at least one possible x such that P(x) proves that "there exists some x such that P(x)"

Direct proof

Showing that P(x) is true for any x proves that "for all x, P(x)"

Zero product propert

If neither of two real numbers is zero, then their product is also not zero.

1. Write the 8-bit binary notation for a.

2. Flip the bits.

3. add 1 in binary notation

How do you convert a positive integer into the two's complement?

Every integer greater than 1 is divisible by a prime number.

Divisibility by a prime number theorem states...

Any integer greater than 1 is either prime or a factor of prime numbers.

Unique factorization of integers theorem states...

An irrational number

A non-terminating real number is

10 (base 2)

1 (base 2) + 1 (base 2) =

11 (base 2)

1 (base 2) + 1 (base 2) + 1 (base 2) =

Set

any collection of well-defined and well-distinguished objects.

Union

If A and B are 2 sets, set C’s elements are elements of A OR elements of B

Intersection

If A and B are 2 sets, set C’s elements are elements of A AND elements of B

Disjoint

Sets A and B are ___ if their intersection is empty

Mutually disjoint

n number of sets are ___ if the intersection of any 2 of them are empty

Difference

if A and B are 2 sets, set C’s elements are elements of A but not elements of B.

Complement

The ___ of a set A relative to the universal set U is the set C of all objects that are not elements of A.

Subset

A is a ___ of B iff every element of A is an element of B

Power set

The ___ A is the se containing all subsets of A

Cartesian Product A x B

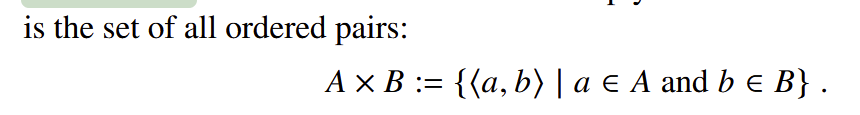
Relation

a subset of a suitably chosen Cartesian product.

Domain

The ___ of a relation Rxy is the set of all x’s for which there is a matching y.

Reflexivity

Rxy, for all x, n = n for all n in x

Symmetry

n = m —> m = n, for any integers n and m

Transitivity

If n = m an m = k, then n = k for for any integers n, m, and k

Equivalence relation

a binary relation that is reflexive, symmetric, and transitive

Function

from A —>B is a relation such that for each element a in A, there is at most 1 element b in B such that <a,b> is an element of F.

Vertical line test

Injective or one-to-one

Different arguments have different function values.

Passes the horizontal line test

Surjective or on-to

Every element of the codomain is a function value

Bijective

both injective AND surjective

Partition

If all subsets of A art mutually disjoint, the subsets form a ___ of A

Argument

A statement claimed to be true and supporting evidence

Probabilistic / Inductive arguments

about things likely to be true

Deductive arguments

If the evidence is true, the claim must be true

Couterexample

A situation that makes the premise true but not the conclusion

Logic

the study of deductive arguments and their validity.

Mathematical Proof

finite sequence of statements and steps such that the statement in each step (except for the last) is either a premise (assumption) or a logical consequence of statements in one or more of the previous
steps; the statement in the last step is a logical consequence of statements made in previous steps

Propositional Logic

studies why and when arguments are valid based entirely on their use of certain sentence-forming expressions (i. e., words or strings of words). To this effect, it fixes the meaning of these expressions and offers rules for their deployment in arguments.

Statement / Proposition

A meaningful sentence to which we can assign a truth value

Truth Functor

Truth-functional sentence operators

Sentence operator

a word or a string of words with one or more blanks such that when the blanks are filled with sentences, the result is again a sentence.

Conjunctor ^

True if conjuncts A AND B are true

Disjunctor v

True if at least 1 disjunct A OR B are true

Subjunctor —>

True if and only if, the antecedent A is false or the consequent B is true

Negator

Flips the truth value

Universal quantifier

the quantifier phrase “for all x it holds that” or, “for all x”. Typically prefixes a subjunction of open sentences

Existential quantifier

the quantifier phrase “There is at least one x such that” or “there is an x”. Typically prefixes a conjunction of 2 open sentendes

Open sentence

A string of words or a phrase with one or more blanks such that a statement results when filling the blank or blanks with a closed term or terms

Direct Proof

A proof without needing to use the negation of the statement A

Direct proof template

A direct proof is a composition of:

Conditionalization and generalization

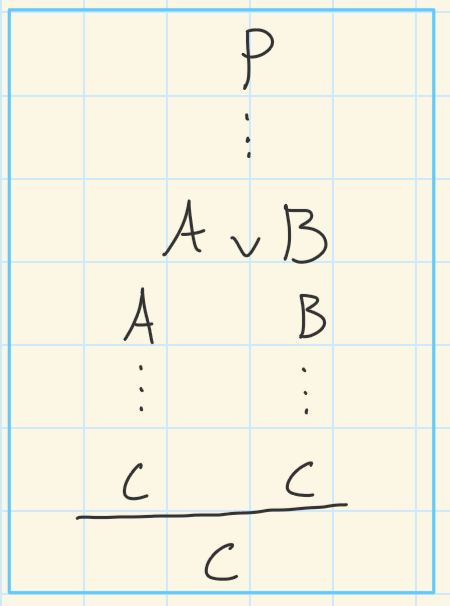
Proof by cases template

Proof by contraposition template

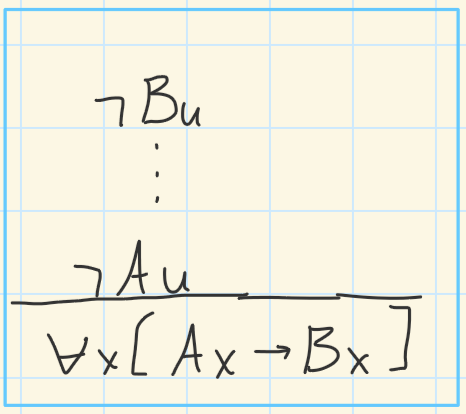
Indirect proof

Proof using the negation of A or B

Proof by contradiction template

The upside down T is an absurdity

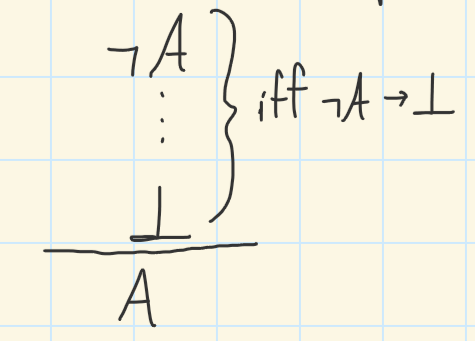
Induction

A template for proving statements that are true for all natural numbers

Induction template

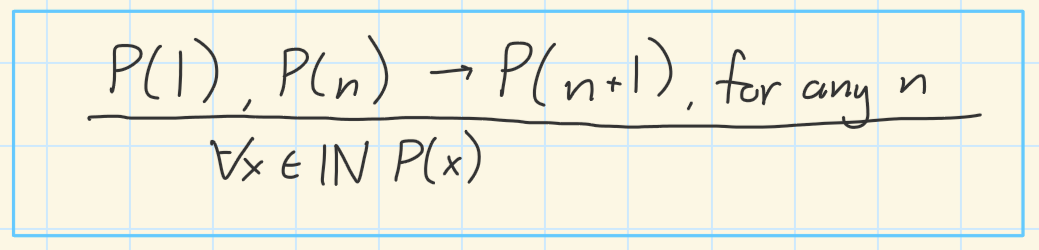
Dedekind’s Axioms

(2 is injective)

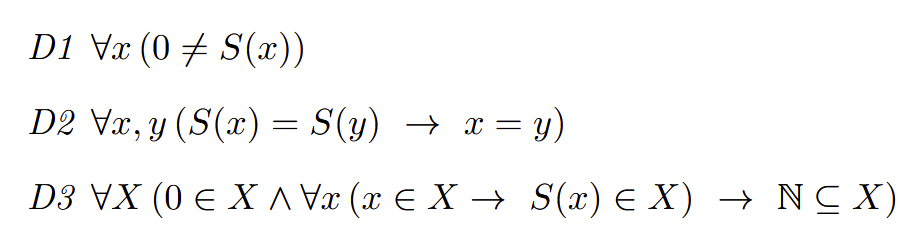
Least element

a is the ___ of ordered-set A if x <= x for all x in A

Well-Order

An ordered set A is ___ -ed if every non-empty subset has a least element

Well-Ordering Principle (WOP)

Every non-empty subset of the natural numbers has a least element.

The set of natural numbers is well ordered

When is the negation of A true?

iff the unnegated statement A is false

Double negation

(works both ways)

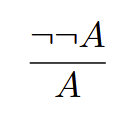
any B; ex falso quodlibet

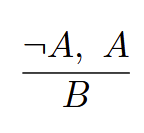
Commutativity for the conjunction

(works both ways)

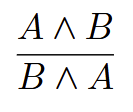
Commutativity for the disjunction

(works both ways)

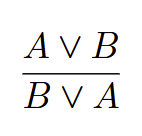
Distribution of the conjunction

(works both ways)

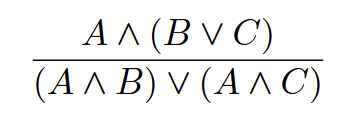
Distribution of the disjunction

(works both ways)

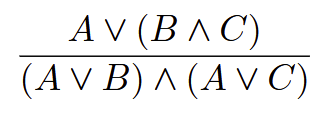
de Morgan conjunction

(works both ways)

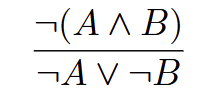
de Morgan disjunction

(works both ways)

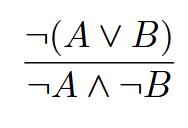
Negation of subjunction

(works both ways)

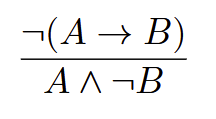
Negation of bi-subjunction

(works both ways)