L3- Fracture Resistance as Energy Release Rate

Fracture energy in an ideal system

twice the surface energy ( must create 2 surfaces during fracture)

i.e. G = 2γ

Fracture energy, G

energy needed to propagate a crack

Equation for energy release rate, G

G = -dΠ/dA

A = area of crack plane ( 2aB)

B = width of plane

P=U_E-F

Gc

measure of the fracture toughness of a material

Equation for Gc (Jm^-2)

Gc= dWs/dA = 2wf

Wf = fracture energy

When will crack growth occur ?

when G = G_c= 2wf

Conditions for stable crack growth

1. G=R

2. dG/da ≤ dR/da

   , R = material resistance to crack extension

   a = crack length

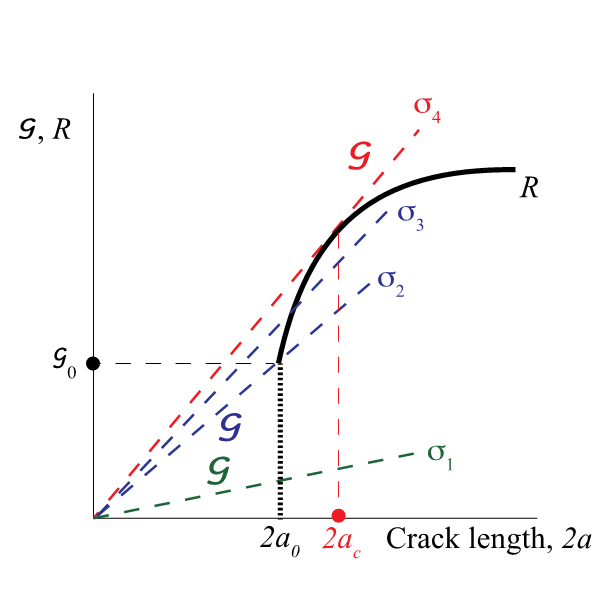
Conditions for unstable crack growth

1. dG/da > dR/da

Assuming 2Wf = R:

Consider 2 possibilities:

1. R = constant + so independent of crack length

2. R increases as crack length increases

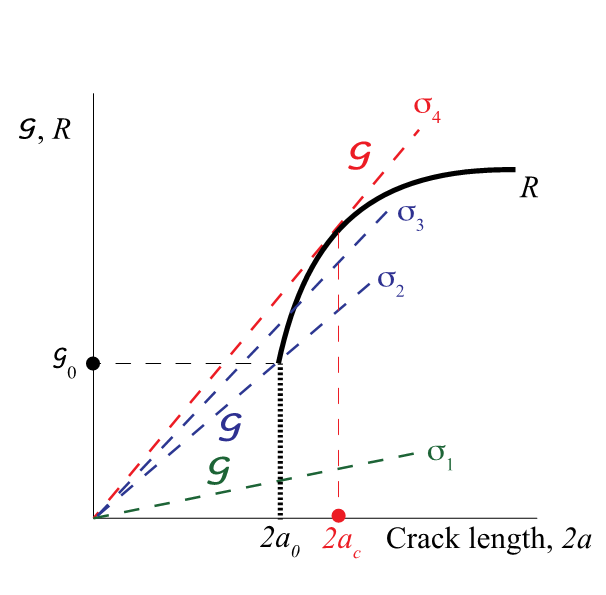
Case 1: R independent of crack size

• If G below R, crack will not grow hence stable until Gc = reached, Gc = R

• At σ2 fracture occurs + crack propagation = unstable i.e. G grows but R stays constant

• 2a_o = defect size

Effect of size of defect on energy release rate, G

The bigger the defect, the greater the energy release rate

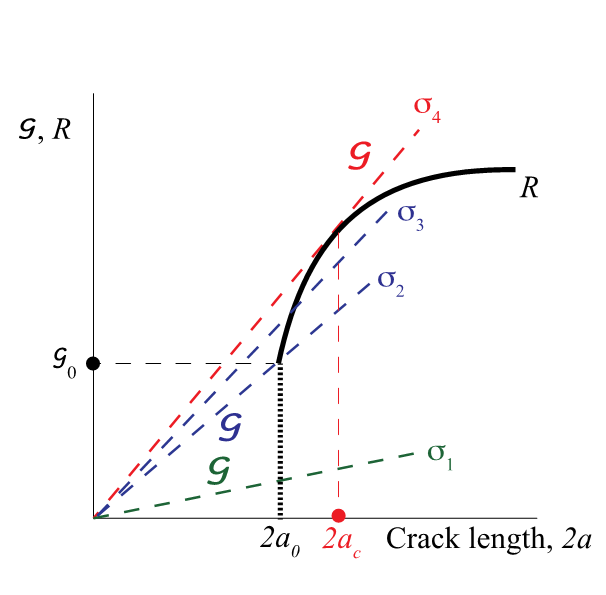
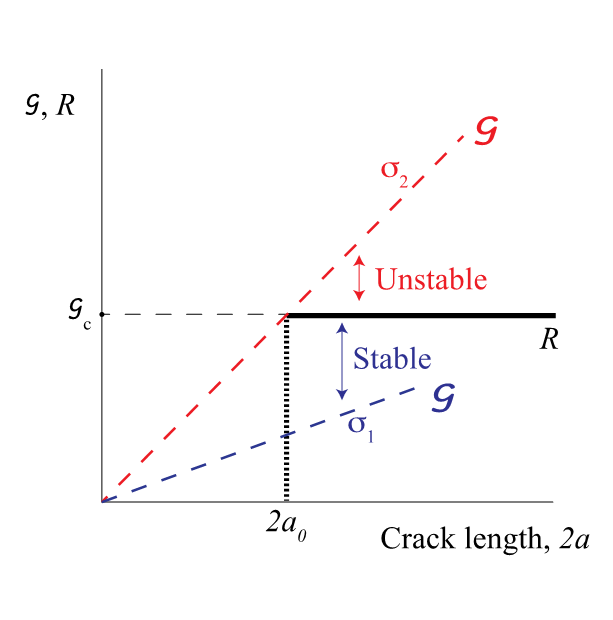
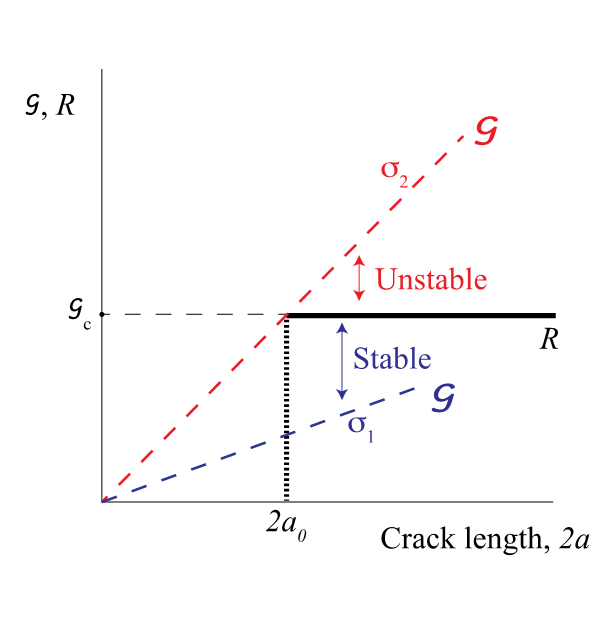
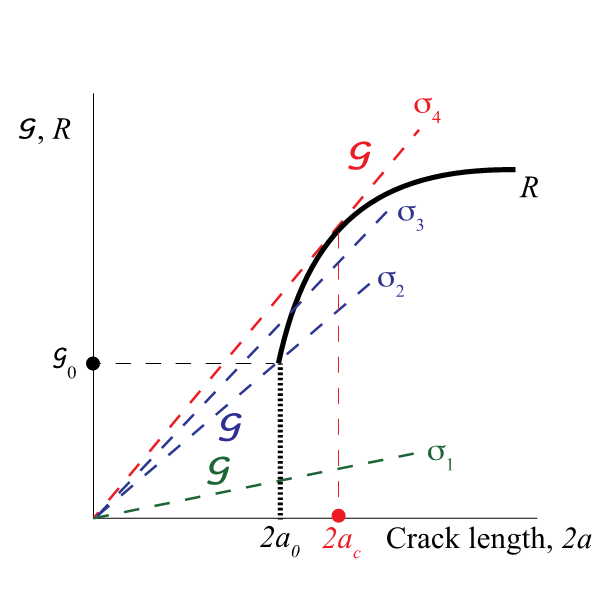
Case 2: R grows with crack size

• For applied σ1, crack = stable

• At σ2 → cracks starts growing but stops as rate of growth of R > G

• At σ3 → crack propagates further but stops immediately as rate of growth R > G

• At σ4 ( critical stress at which crack = unstable) → crack unstable as G grows faster than R.

Types of fracture in polycrystalline materials:

1. Transgranular/intragranular

2. Intergranular

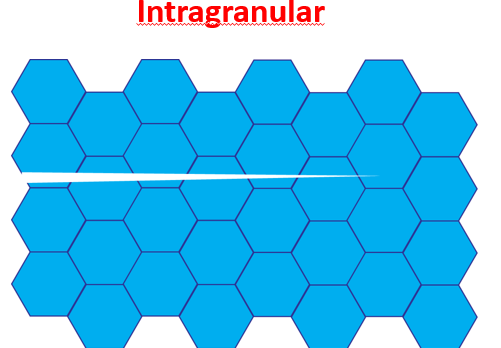
Transgranular/intragranular fracture

Crack propagates across grains

Intergranular

Crack propagates along grain boundaries

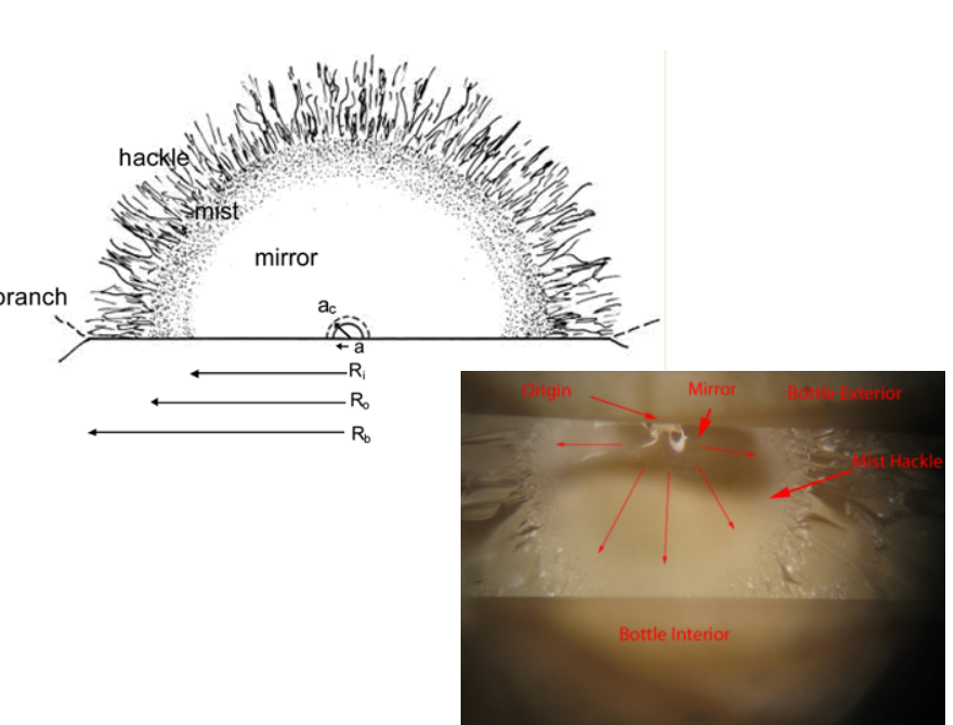
3 zones in fracture surfaces

1. Mirror

2. Mist

3. Hackle

Mirror

• smooth regions surrounding + centred on fracture origin

Mist

• Markings on surface of accelerating crack close to term velocity

• First has misty appearance

• As v increases, fibrous texture, elongated in direction of cracking

Hackle

• A line on surface, running in local direction of cracking

• separating parallel but noncoplanar portions of crack surface

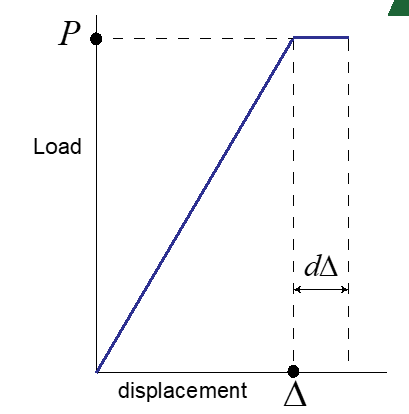
Load control

If the thickness of the sample is B, dA=Bda

Then

G=1/B (dU_E/da) at constant P=P/2B (d∆/da) at constant P

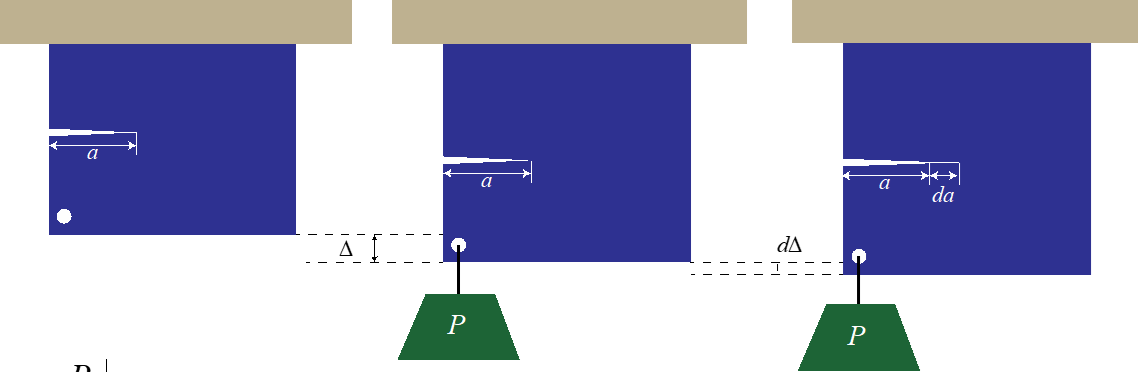
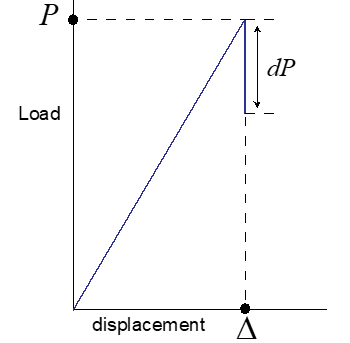
Displacement control

• Recording how load changes as crack grows

• G=-1/B (dU_E/da) const∆=-∆/2B (dP/da) const∆

  B = thickness

Compliance

Inverse of stiffness

Eqn for Compliance

• ∆/P

  ∆ = displacement

  P = load

Equation for G in load/ displacement control