AP Calculus BC - Unit 1 MCQ Bank

Hlahla said 10 of these would show up on the test.

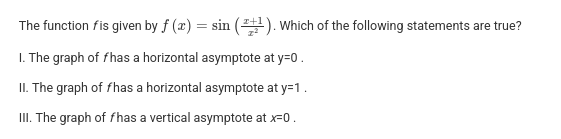
The function f is given by

. Which of the following statements are true?

I. The graph of f has a horizontal asymptote at y=0 .

II. The graph of f has a horizontal asymptote at y=1 .

III. The graph of f has a vertical asymptote at x=0 .

A. I only

The graph of which of the following equations has y=1 as in asymptote?

C. y = (x)/(x+1)

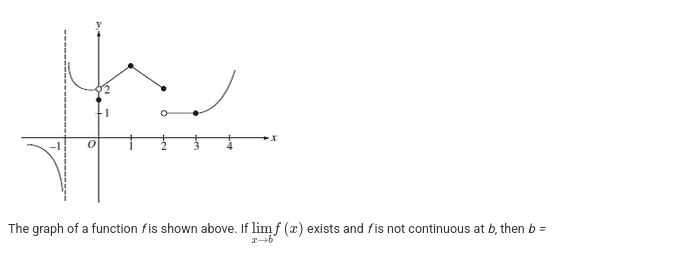
The graph of a function f is shown above. If LIM exists and f is not continuous at b, then b =

B. 0

Let f be a continuous function on the closed interval [-3,6]. If  f(-3)=-1 and f(6)=3, then the Intermediate Value Theorem guarantees that

D. f(c)=1 for at least one c between -3 and 6

Let f be a function that is differentiable on the open interval (1,10) . If f(2)=-5, f(5)=5, and f(9)=-5, which of the following must be true?

I. f has at least 2 zeros.

II. The graph of f has at least one horizontal tangent.

III. For some c, 2<c<5, f(c)=3.

E. I, II, and III

Let g be a continuous function on the closed interval [0,1]. Let g(0)=1 and g(1)=0. Which of the following is NOT necessarily true?

D. There exists a number h in [0,1] such that g(h) = 3/2

Let f be the piecewise function defined above. Which of the following statements is false?

C. f is continuous at x=3.

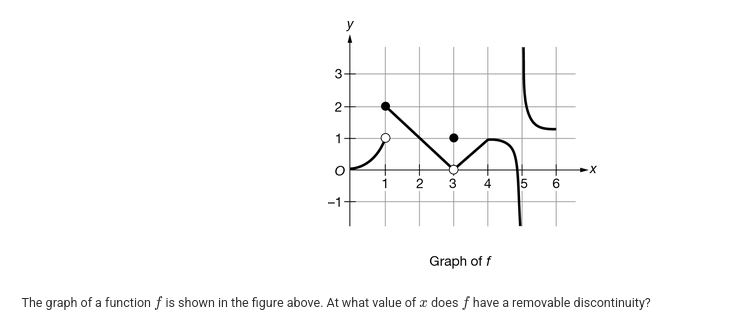
The graph of a function is shown in the figure above. At what value of does have a removable discontinuity?

B. x=3

Let F be the function defined above. Which of the following statements is true?

B. f is not continuous at x=1 because f(1) does not exist.

f(3) = -1

x=5 and x=0 only

g(x) = 0 has at least two solutions in the interval [2,4]

f(x) = 12.235

f is continuous for all x.

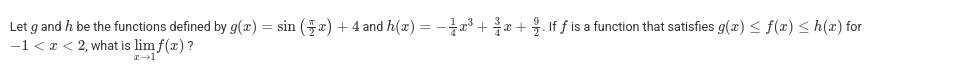
5

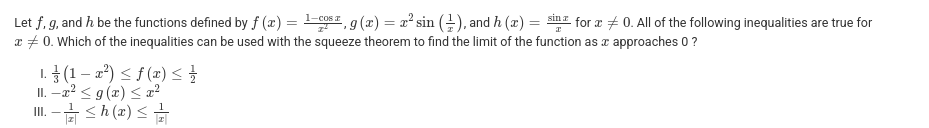
II only

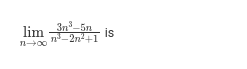
3

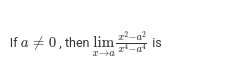
1 / 2n²

II and III only

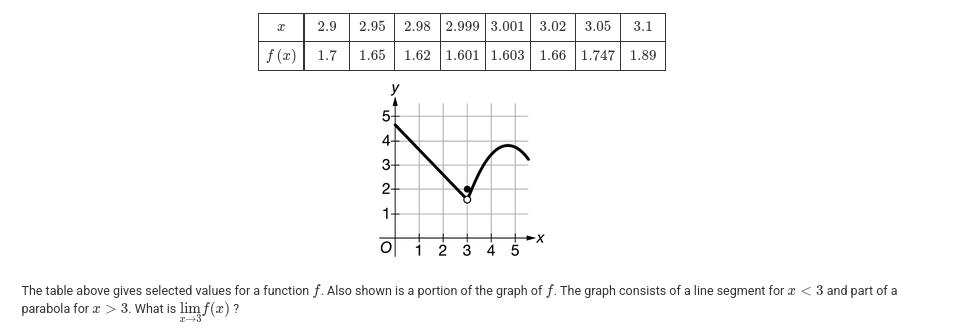
1.6