Discrete Math Unit 1

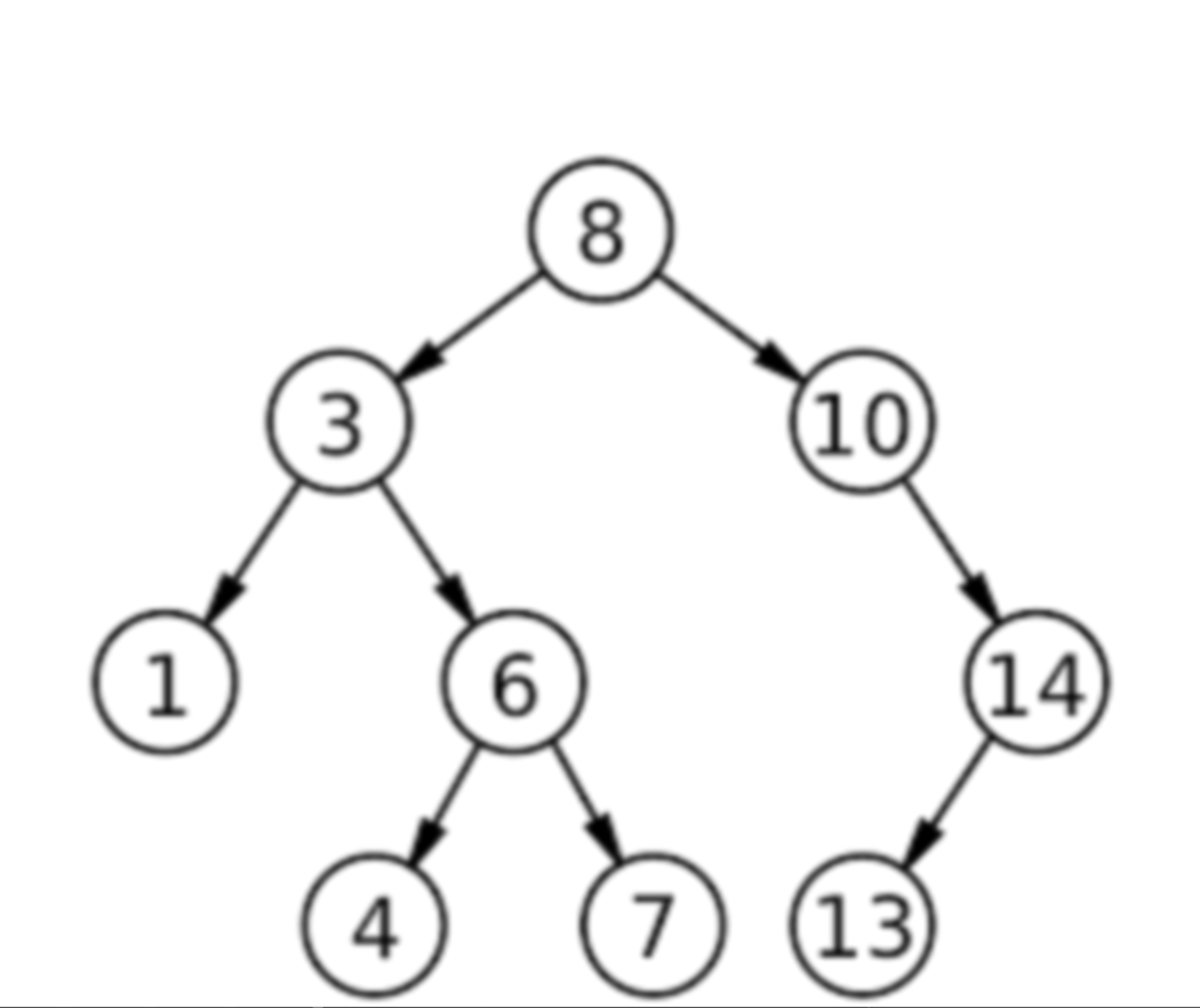
Looking at the example tree, how can you tell what kind of tree it is?

It’s a binary tree because every node has at most two children. (If any node had 3+ children, it would be a general k-ary tree.)

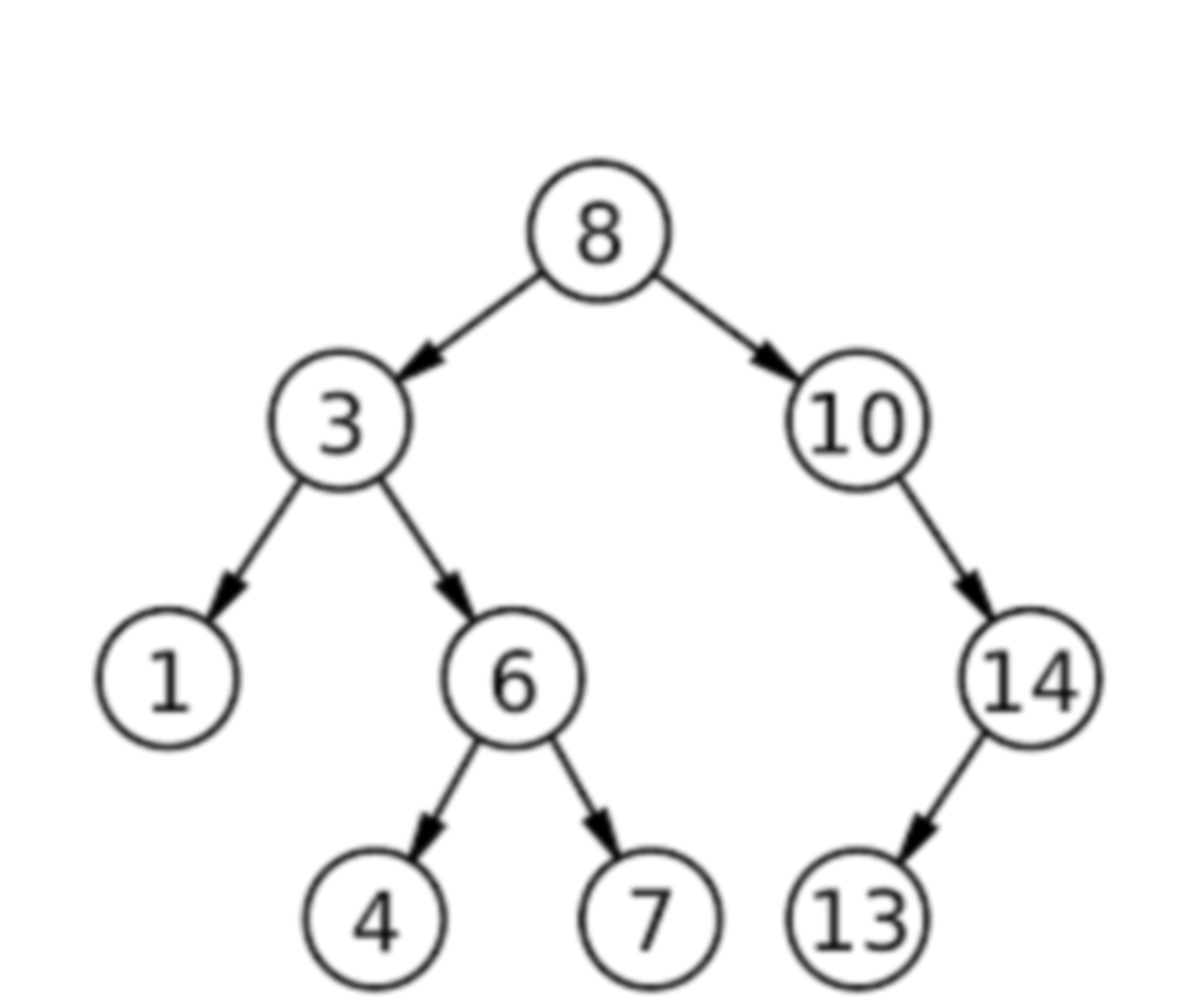
By inspecting the example tree, how many total vertices (nodes) does it contain?

9 vertices—just count each circle: 8, 3, 10, 1, 6, 14, 4, 7, 13.

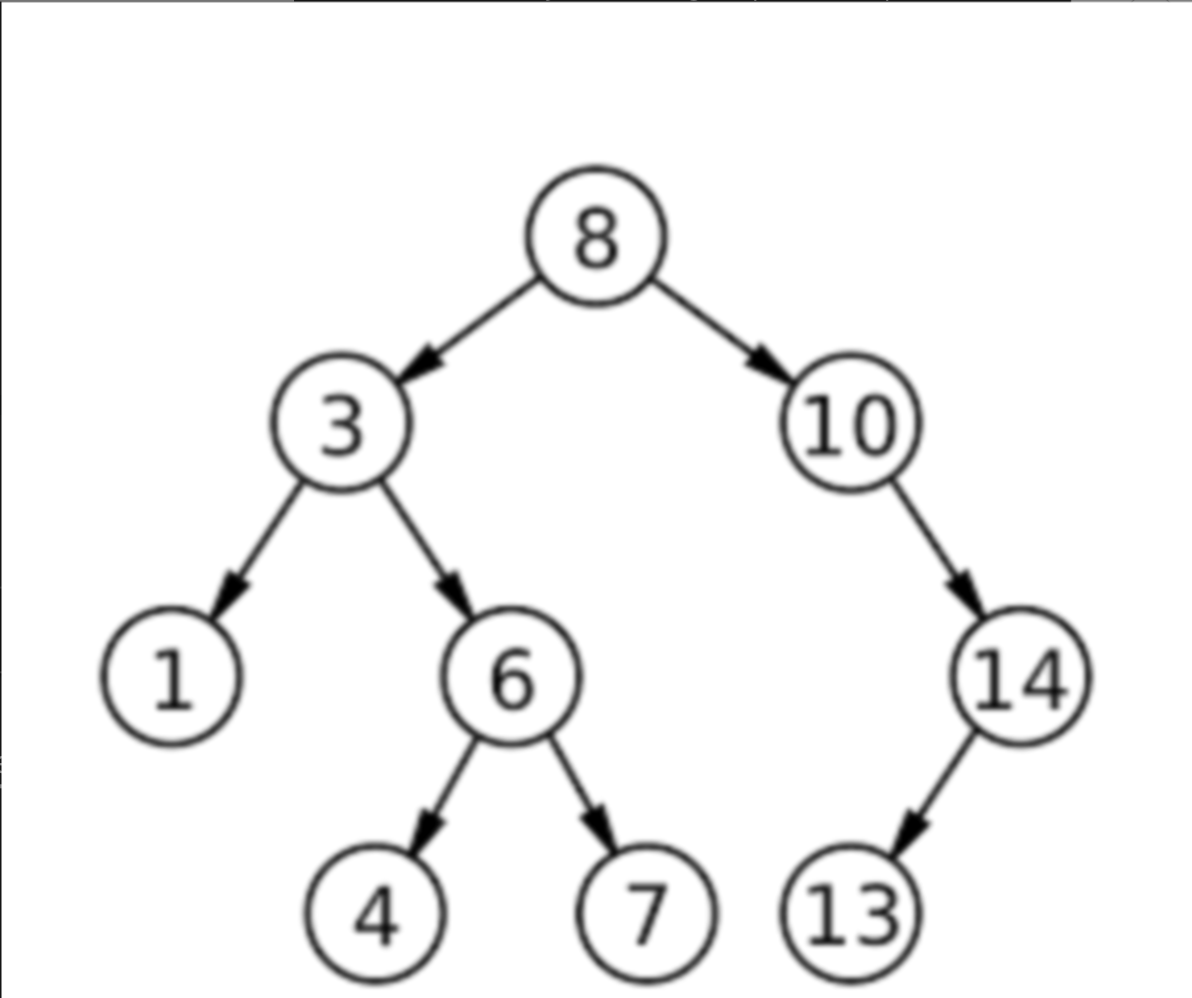
Given that there are 9 vertices, how many edges must the example tree have?

• 8 edges—every tree with n vertices has exactly n – 1 edges (9 – 1 = 8).

An edge is the connection (the line) between a tree and a node.

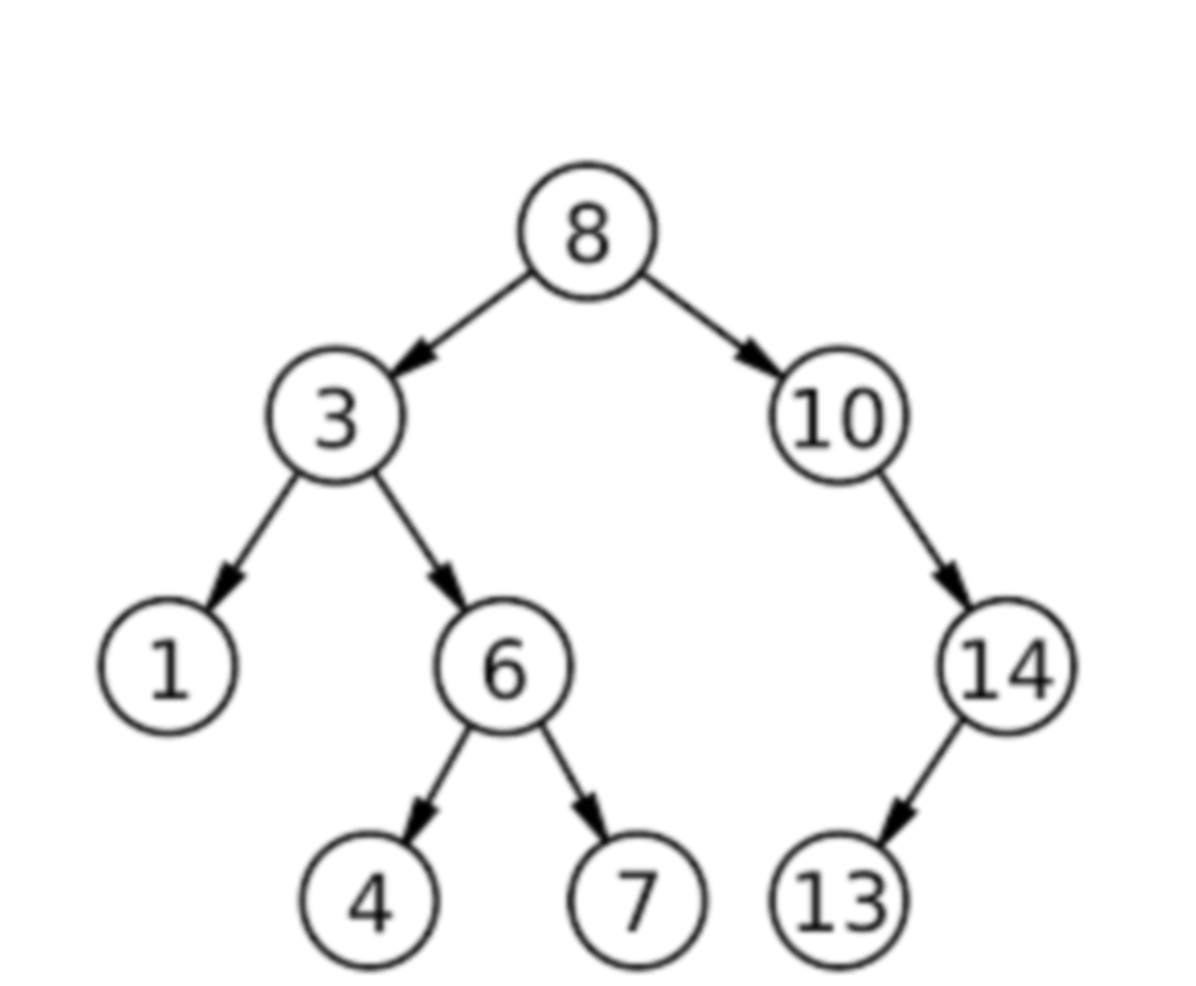
Which nodes in the example tree are its leaves?

1, 4, 7, 13—leaves are nodes with degree 0 (no children)

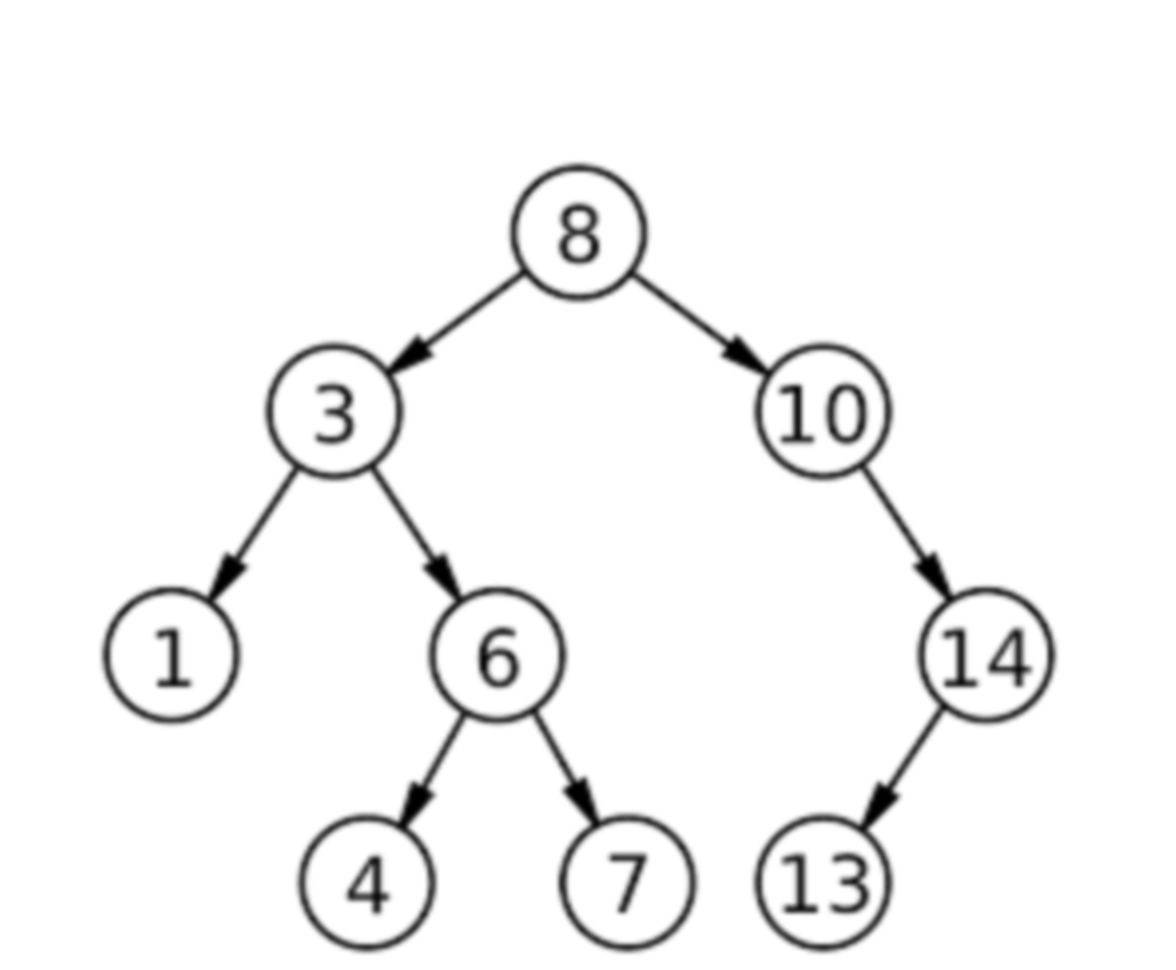
What is the height of the example tree?

3—height is the max number of edges on any root-to-leaf path (e.g., 8→10→14→13 has 3 edges).

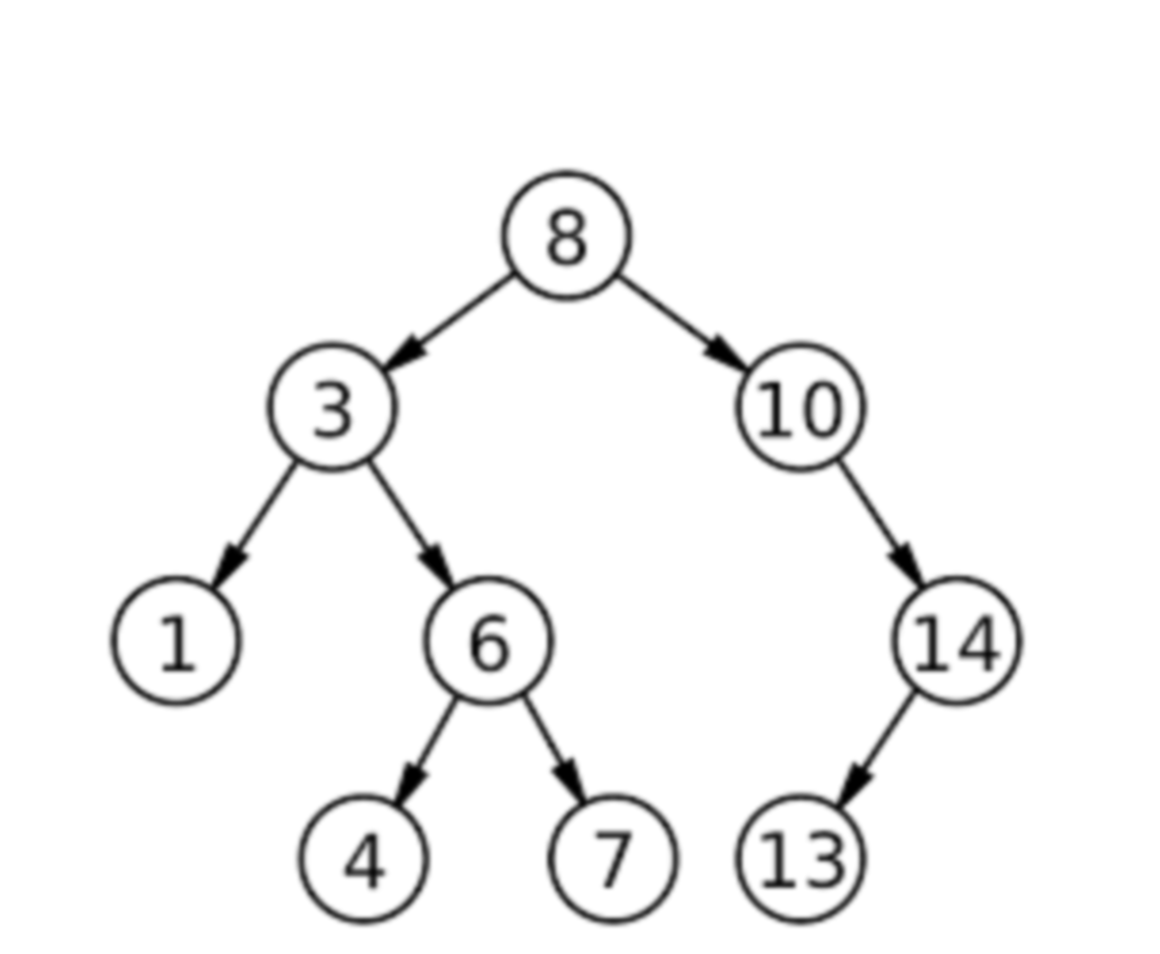
Is the example tree height-balanced? Explain how you know.

Yes. For every node, the heights of its left and right subtrees differ by at most 1. (Check each node’s subtree heights.)

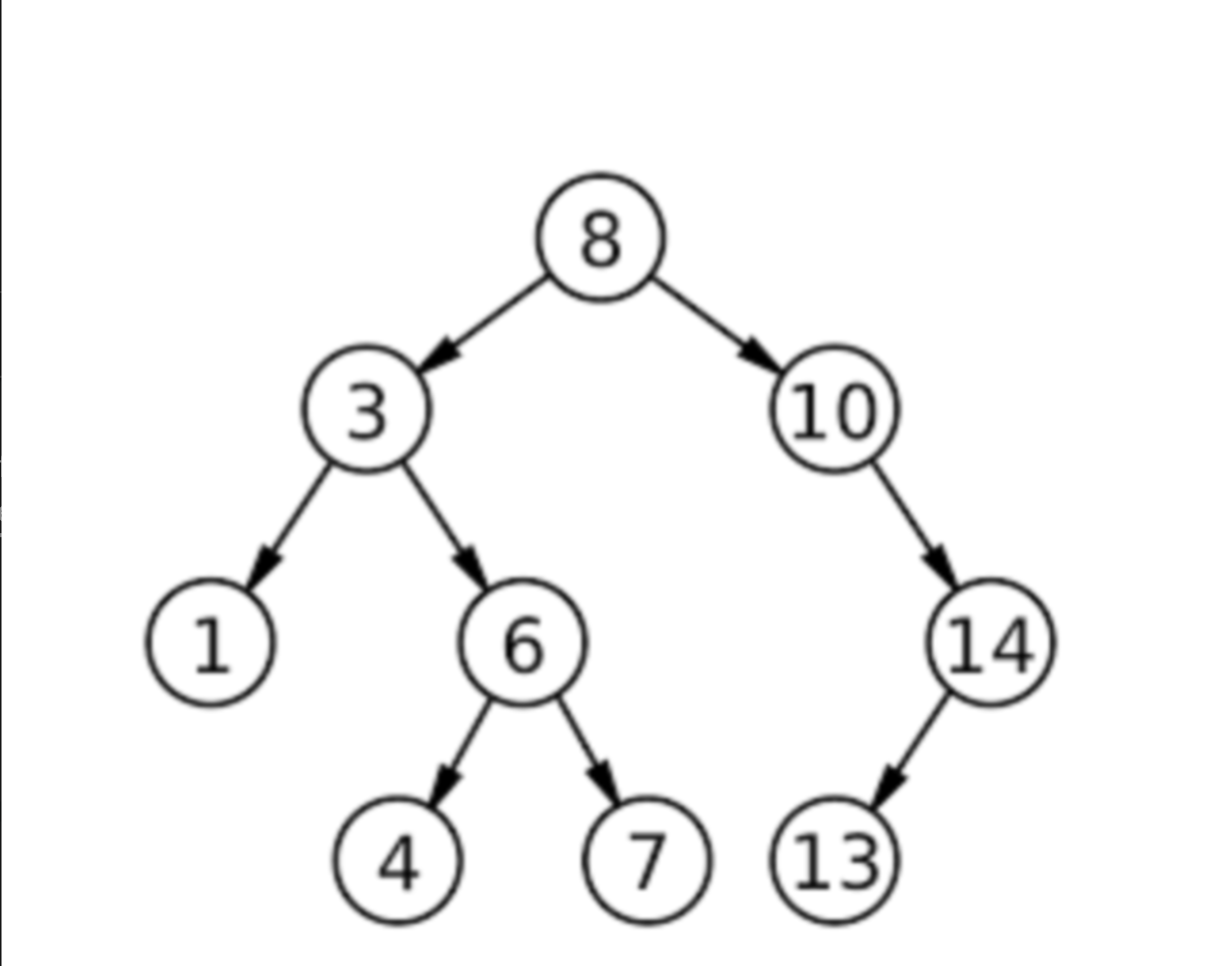
Is the example tree a complete binary tree? Why or why not?

No. A complete tree fills each level left-to-right; here node 10 has a right child (14) but no left child, leaving a gap

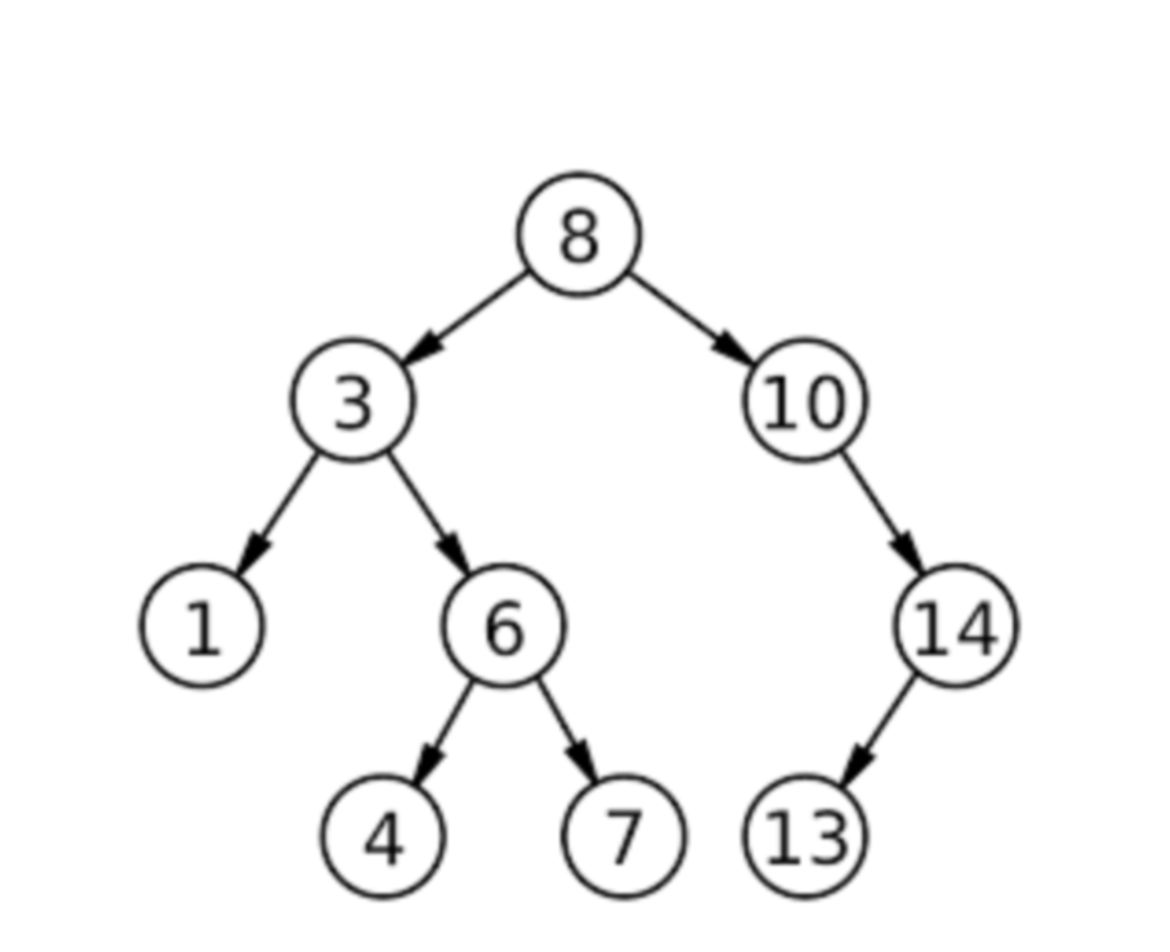
What sequence do you get from a preorder traversal of the example tree?

8, 3, 1, 6, 4, 7, 10, 14, 13
(Visit Root → Left subtree → Right subtree.)

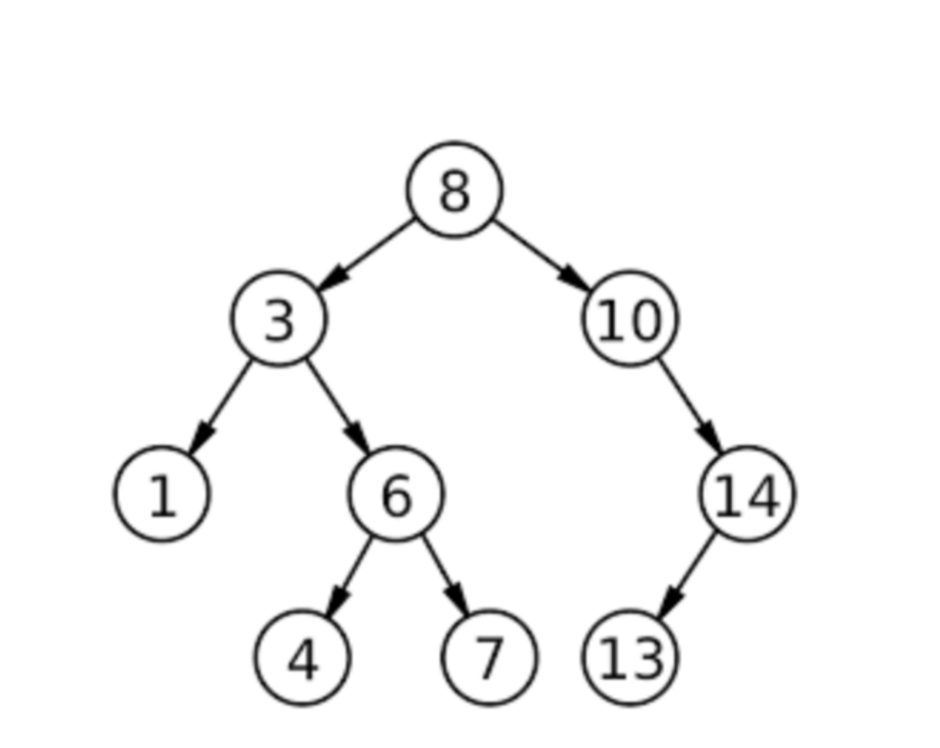
What is the postorder traversal of the example tree?

Back: 1, 4, 7, 6, 3, 13, 14, 10, 8
(Visit Left → Right → Root.)

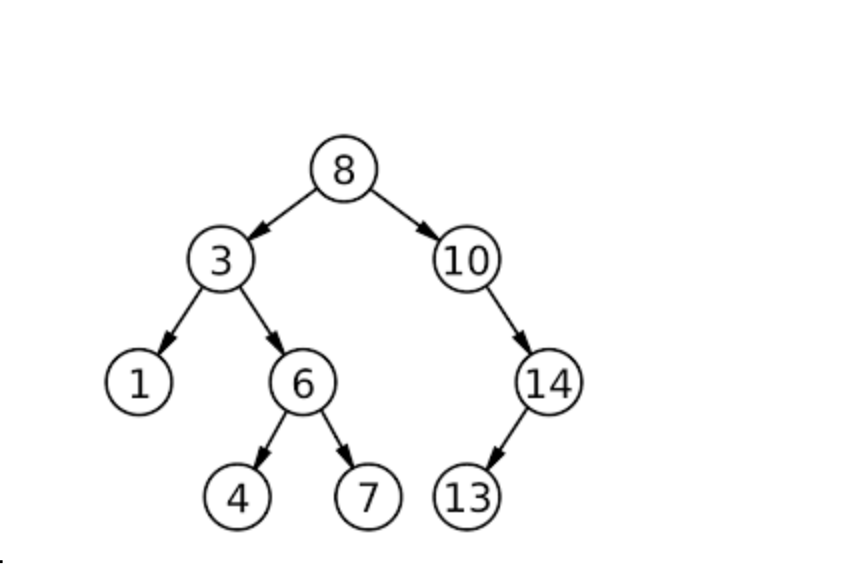
What list results from an inorder traversal of the example tree?

1, 3, 4, 6, 7, 8, 10, 13, 14
(Visit Left subtree → Root → Right subtree.)

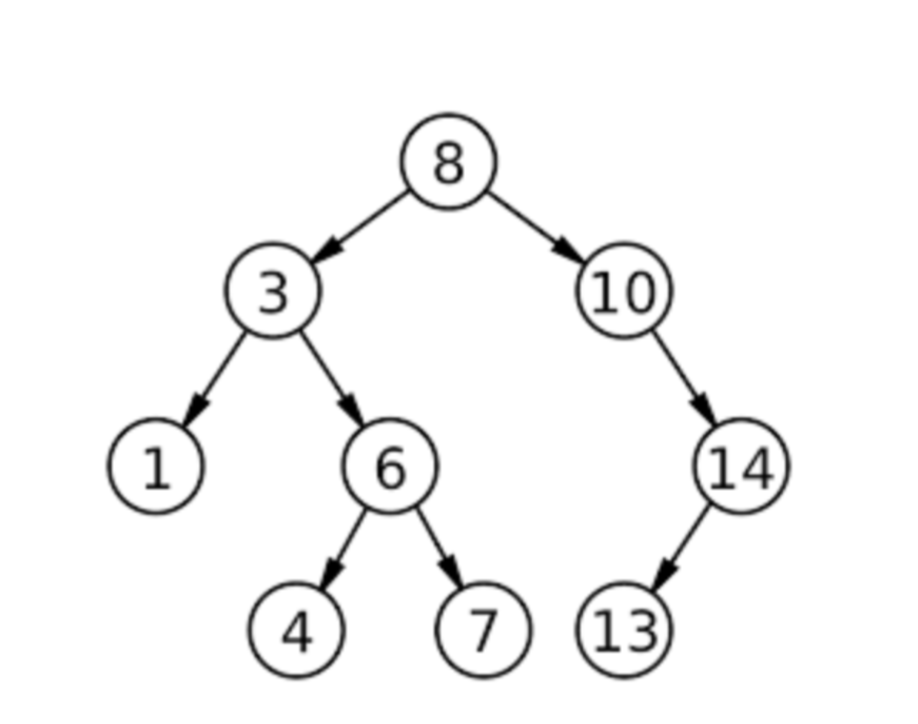
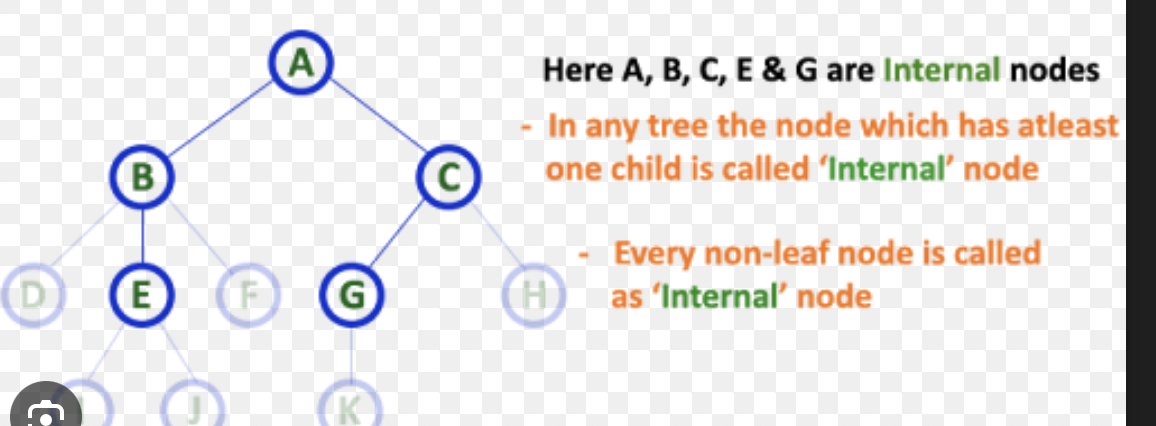
Which nodes in the example tree are internal nodes, and how do you identify them?

• Internal nodes are those with degree ≥ 1 (at least one child).

• Scan each node’s children pointers.

• Here they are: 8, 3, 6, 10, 14.
  But if a node has zero children, it’s a leaf, not internal

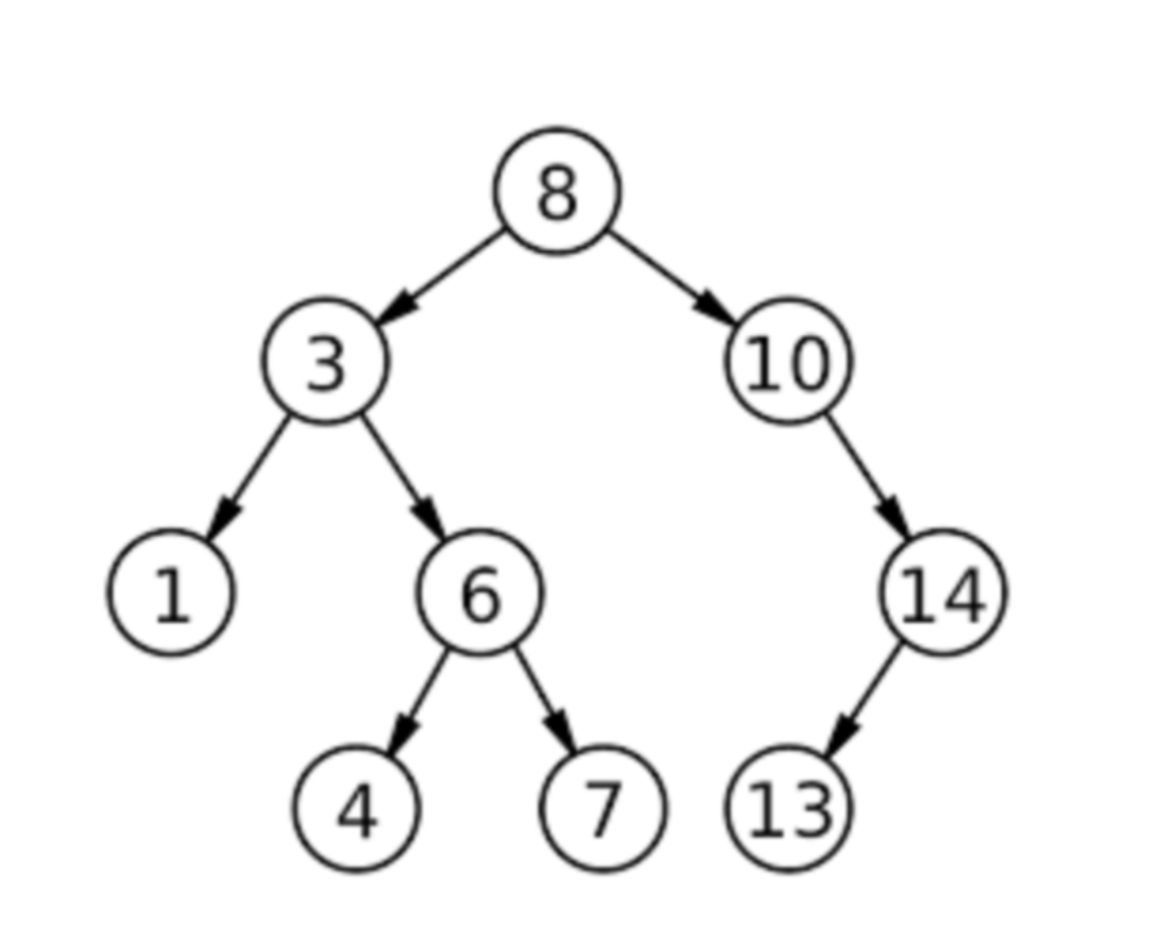
What is the depth of node 7 in the example tree, and how do you compute depth?

1. Depth(node) = number of edges from the root to that node.

2. Trace path root→…→7:
   8 → 3 → 6 → 7

• has 3 edges

• So depth(7) = 3.
  But if you counted nodes instead of edges, you’d get 4, which is the level (levels = depth+1).

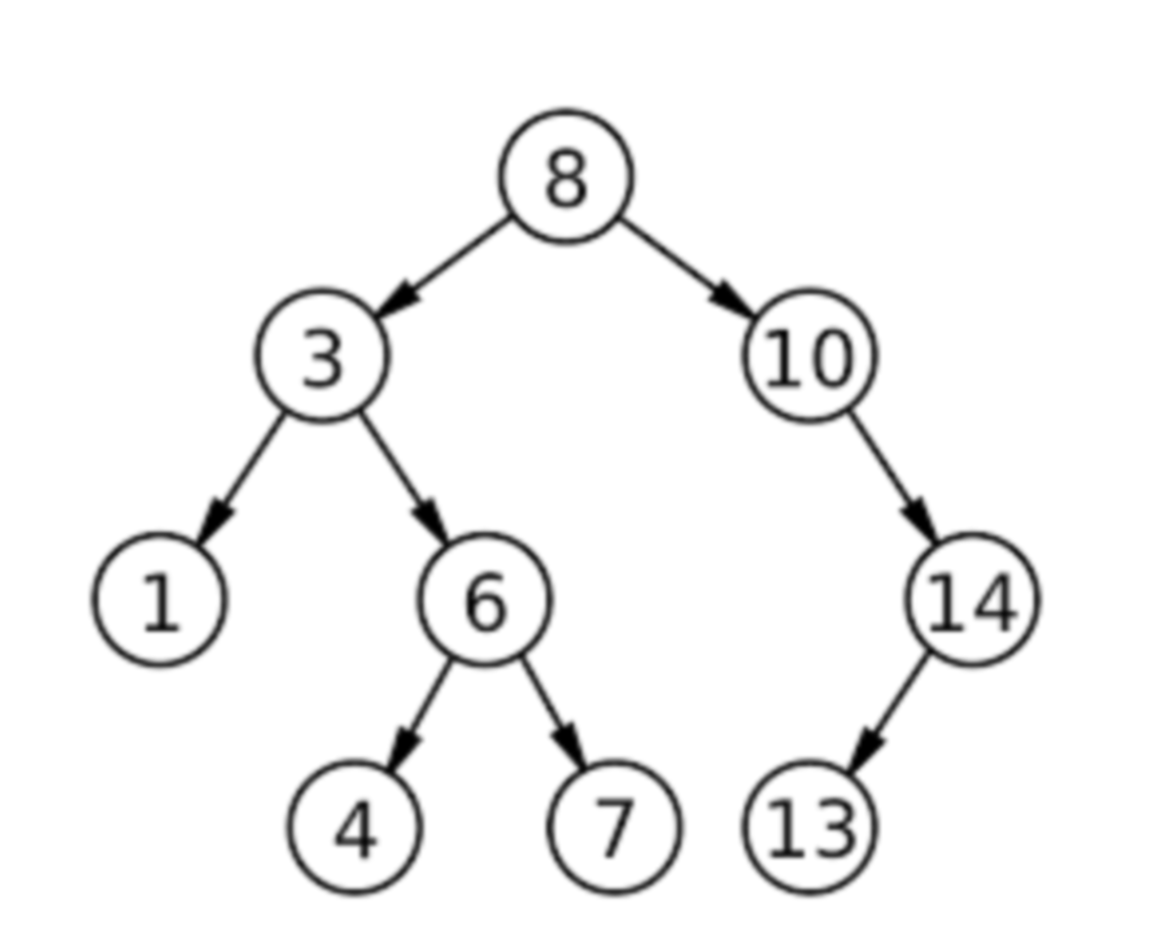
How many levels does the example tree have, and how is that related to height?

1. Number of levels = height + 1 (root sits on level 1).

2. We know height = 3 → levels = 4.

3. Levels:

   • Level 1: {8}

   • Level 2: {3, 10}

   • Level 3: {1, 6, 14}

   • Level 4: {4, 7, 13}
     But if you defined the root as level 0, then levels = height + 0 = 3 + 0 = 3 instead.

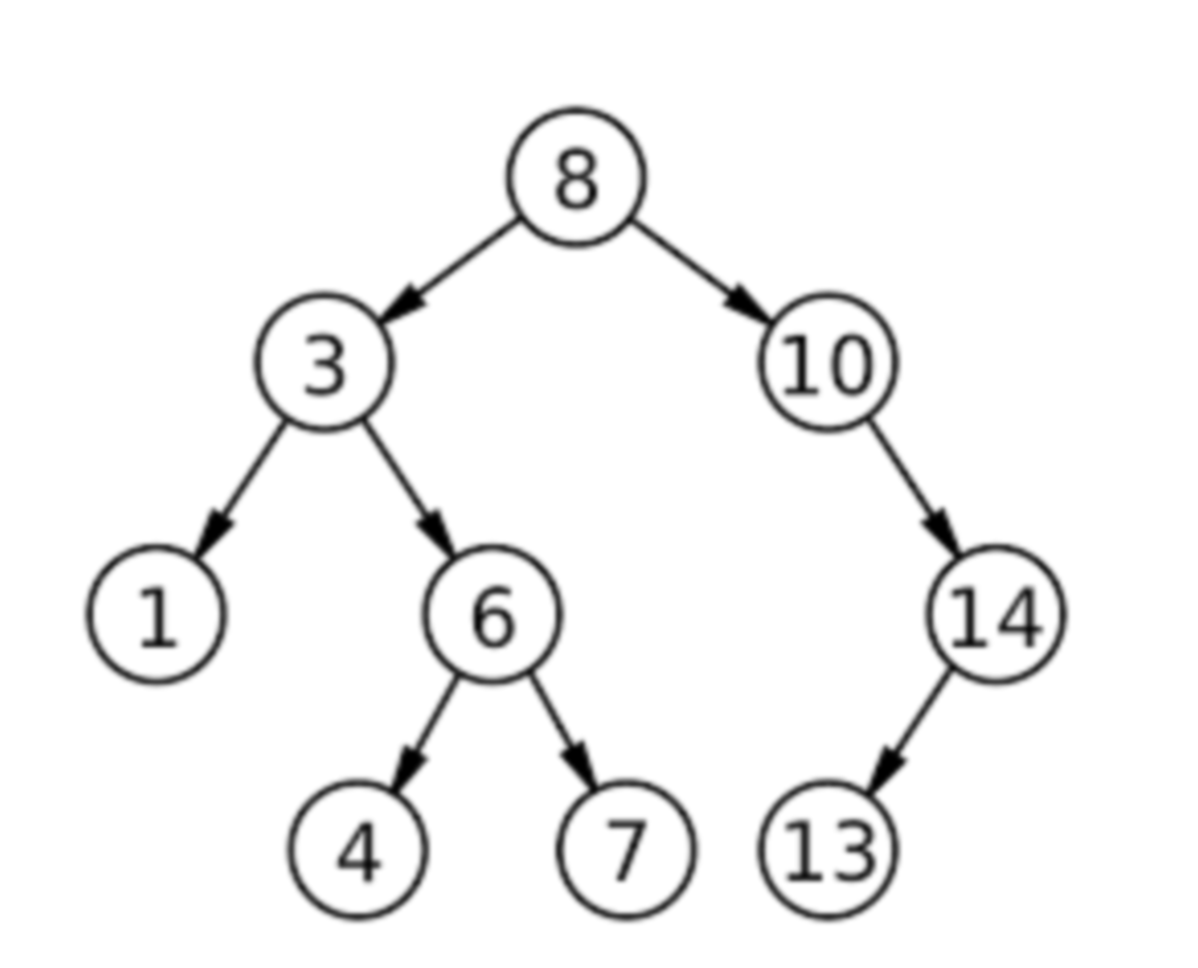
What is the degree of the root (node 8) in the example tree, and why does that matter?

]

1. Degree = number of children.

2. Root 8 has two children (3 and 10) → degree(8) = 2.

3. This tells you immediately it’s not a leaf and that the overall tree has arity ≥ 2.
   But if degree(8) were 1, it’d have only one subtree and the shape would skew left or right.