ELEC 825 Week 1

basics of ML with a focus on linear classifiers, Naive Bayes, and SVM

n-fold cross validation

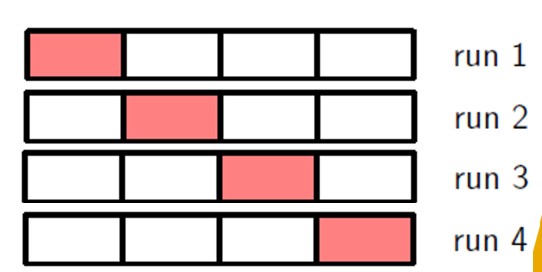
n-fold cross validation

• solves problem of noisy estimate of predictive performance when there isn’t enough data for validation

1) split training data into n folds

2) in each run, train on n-1 folds and validate on the remaining 1 fold

3) repeat (2) n times

4) calculate the average performance on the n validation folds

5) select the model that achieves the best average performance

what are the 3 main phases in solving ML problems?

1) training: learning the models.

2) validation: selecting models.

3) testing: evaluating the models you finally obtained above

support vectors

examples closest to the hyperplane

margin

distance between support vectors

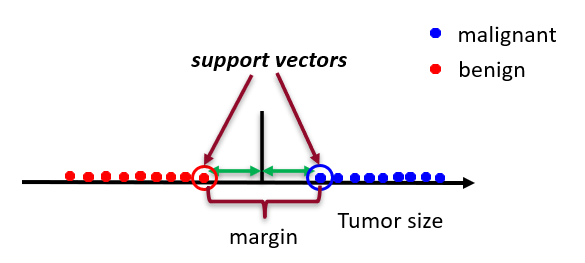
support vector machine (SVM)

maximum-margin classifier that maps data to a higher dimension space (implicitly using kernel)

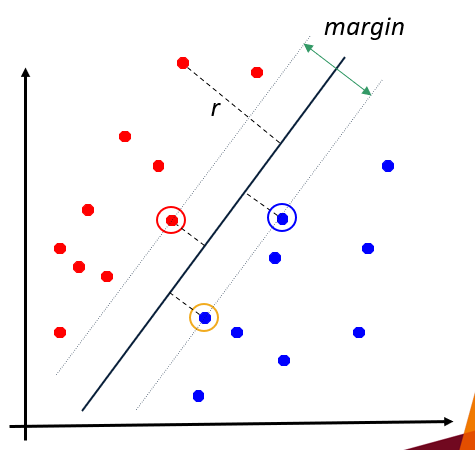
how do you reduce sensitivity to outliers?

by allowing misclassification during training → bias/variance tradeoff

when is the margin largest?

when the hyperplane is halfway between the 2 samples

how do you classify datasets that aren’t linearly separable?

represent the data into a richer (larger) space which includes some fixed, possibly nonlinear functions of the original inputs/measurements

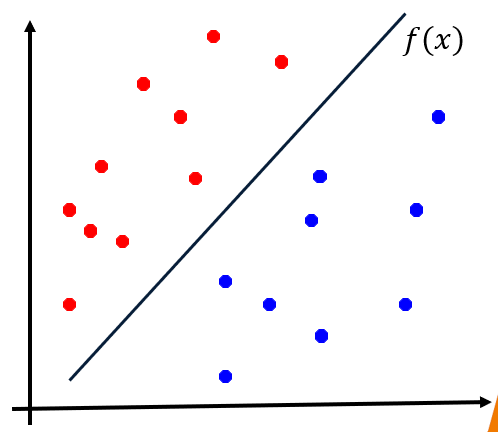
linear classifier

find the line (or hyperplane) which can “best” (under some criterion/objective) separate two classes:

𝑦(𝑥)=𝑊^𝑇 𝑥+𝑏

what are the differences between regression and classification?

1) regression tries to predict a number while classification predicts a category

2) regression identifies many possible outputs while classification only has a small number of possible outputs

machine learning

computer receives the input and expected output to write a program for solving the problem

when do we need machine learning?

when a) human expertise does not exist, b) models are based on huge amounts of data, c) humans can't explain their expertise, d) models must be customized

supervised learning

given training samples and corresponding desired

outputs (labels), predict outputs on future inputs

what are some examples of supervised learning?

classification, regression, time series prediction

unsupervised learning

• given training samples without desired outputs, automatically discover representations, features, structures, etc.

• learn a function f(x) to explore the hidden structure of x

what are some examples of unsupervised learning?

clustering, low-dimensional manifold learning

reinforcement learning

given sequences of states and actions with

(delayed) scalar rewards/punishments, output a policy

what are some examples of what a learning algorithm can do?

recognizing patterns, generating patterns, recognizing anomalies, prediction

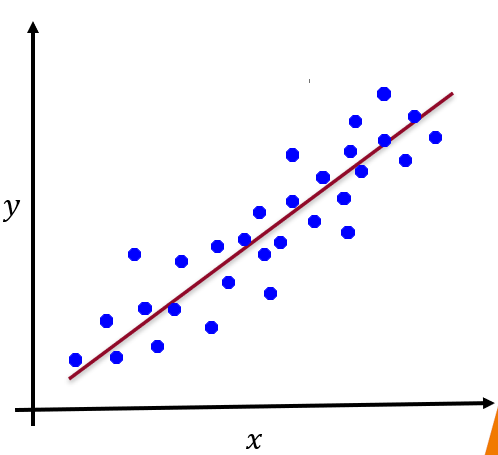
regression

given {x_i, y_i} where x_i E R^D (set of all vectors with d real components) and y_i is a real value, learn a function f(x) to predict y given x

classification

given {x_i, y_i} where x_i E R^D (set of all vectors with d real components) and y_i is categorical, learn a function f(x) to predict y given x

representation learning

• a form of unsupervised learning that learns a good representation for the inputs, which is then used for subsequent supervised or reinforcement learning

• compact and low-dimensional representation for inputs

outlier detection

a form of unsupervised learning that detects highly unusual cases from the given data

rule learning

a form of unsupervised learning that learns rules from the data

feature space

multidimensional space where each dimension represents a different feature or characteristic of data

feature normalization

process of transforming numerical features to a standard scale, usually between 0 and 1, to ensure fair comparison and prevent dominance of certain features in machine learning models

what are the steps to Naive Bayes Theorem for discrete features?

1) sort data cases into bins according to Ck

2) compute class prior p(Ck) using frequencies

3) for each class, estimate the distribution of ith variable/feature: 𝑝(𝑥_𝑖│𝐶_𝑘 )

4) compute the posterior

how do you deal with continuous features if using Naive Bayes Theorem?

discretization OR fit a known distribution