Momentum and Impulse

MEE1008: Dynamic Systems - Lecture 17

Law of conservation of momentum

The momentum of a system is constant if no external forces are acting on the system.

m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂

Conservation of momentum and Newton’s First Law

An object that continues to maintain its state of rest or motion unless or until it is acted upon by an external force.

Conservation of momentum and Newton’s Third Law

A force applied by an object A on object B, object B exerts back an equal force in magnitude, but opposite in direction.

Change in momentum

m(v - u)

Conservation of momentum equations

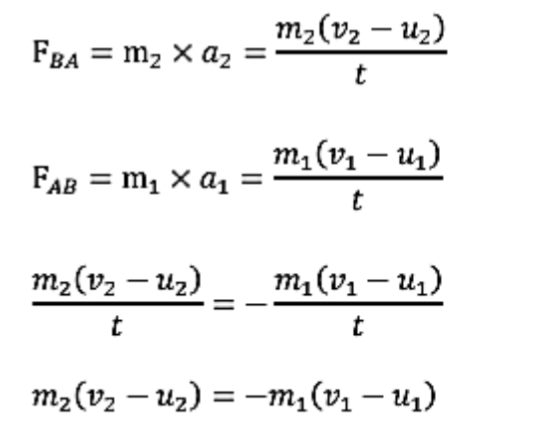
Impulse

The force acting on an object and the time interval the force is exerted.

Impulse - momentum theorem

The impulse applied to an object will be equal to the change in its momentum.

F_average = m(v₂ - v₁)/Δt

Newton’s Second Law and linear momentum

The resultant (net) force is proportional to an object’s rate of change in linear momentum.

Linear momentum

G = mv

Resultant force and linear momentum

ΣF = d(mv)/dt = dG/dt

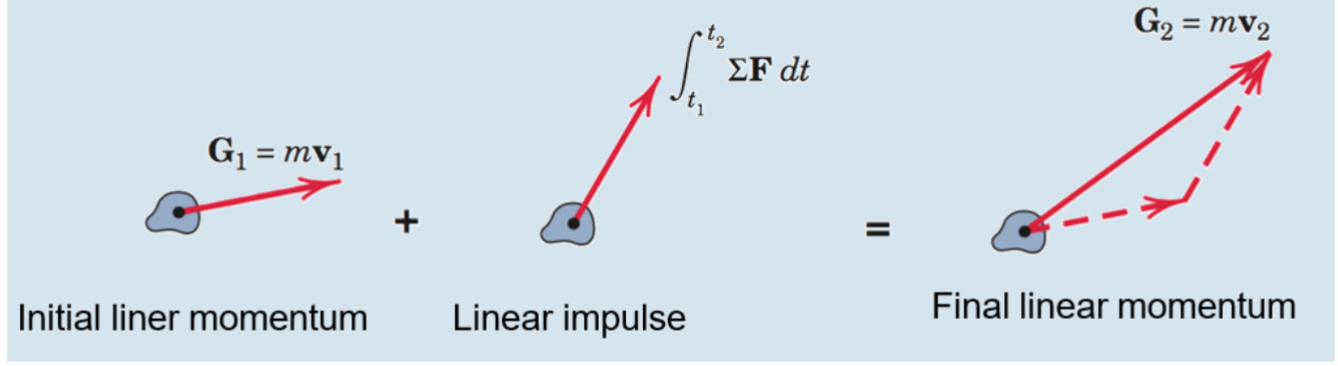
Linear impulse-momentum principle

G₁ + ∫ΣF dt = G₂

where the integral is constrained by t₁ and t₂.

Linear impulse - momentum principle in components

m(v₁)_x + ∫ ΣF_x dt = m(v₂)_x

m(v₁)_y + ∫ ΣF_y dt = m(v₂)_y

m(v₁)_z + ∫ ΣF_z dt = m(v₂)_z

Use of the linear impulse - momentum principle

Provides a direct means of obtaining the particle’s final velocity v₂ after a specified time period when the particle’s initial velocity v₁ is known and the forces acting on the particle are either constant or can be expressed as functions of time.

Finding v₂

Apply ΣF = ma to obtain a, then integrate a = dv/dt to obtain v₂.

Impulse - momentum diagram

Conservation of linear momentum

If the resultant force on the particle is zero, i.e. ΣF = 0.

G₁ = G₂

In this case, the linear momentum of the particle is said to be conserved.

Applications of impulse momentum

Pitching machine

Crane mounted hammer