Language Variation

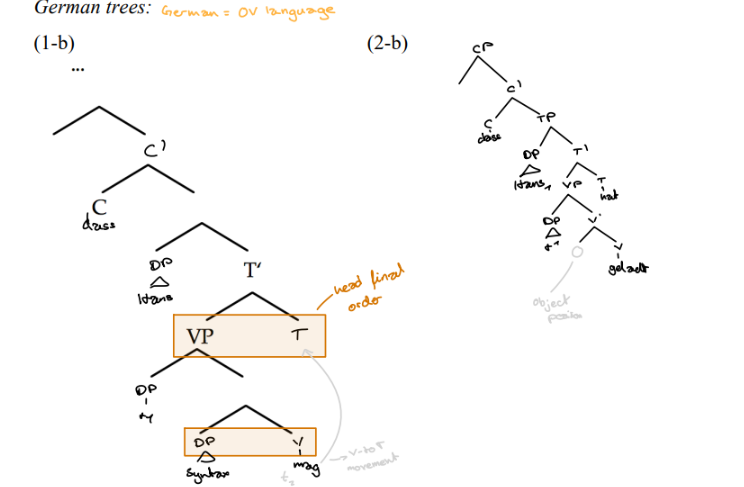
The Head Parameter in English and German

The word order differs in Embedded clauses

→that John has laughed / dass Hans gelavht hat

V2 Parameter which holds in German but not English (finite full verb is alway 2nd constituent)

Different setting of the head Parameters

E: all phrases head initial

D: TP and VP head-final

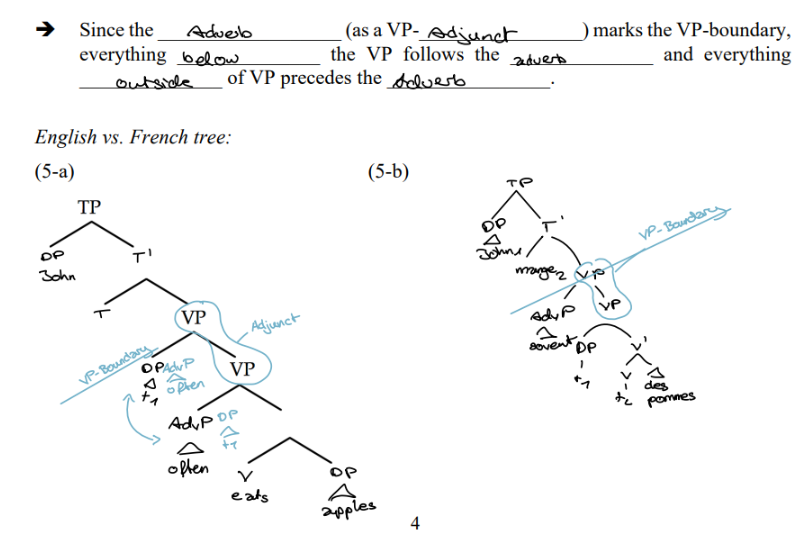
The Verb Raising Parameter in English and French

The word order differs if there is an Adverb (& finite full verb)

E: FfV follows Adverb

F: FfV precedes Adv

With auxilliary:

E: Aux aslo precedes Adv

F: If main verb is non-finite it does not preceede the Adverb

Verb raising parameter: V-to-T movement of the finite full verb

Question formation in E vs D

Question formation often involves inversion (cf. what will you do?). Technically, this is T-to-C movement. If there is an auxiliary, it moves from T to C; but what happens if there is no auxiliary around?

D: Was liest du → movement of finite verb from V via T to C (not available in E = violates head movement constraint: don`t skip a head position)

E: What do you read → Do-suport as a last resort strategy

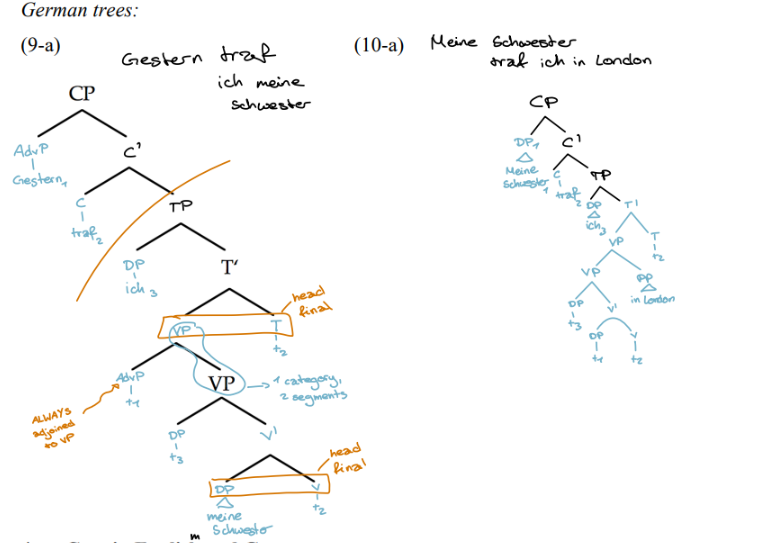
The V2 Parameter in English and German

Word orders differ in main clauses (germna is assymetric V2 language)

E: subject must precede the finite Verb

D: finite verb must be in second position

technical implementation:

X’ theory: verb mvt to C (via T); first constituent moves to Spec

P&P theory: V2 parameter holds in G but not E

structural case

is licensed in a particular structural configuration

if a structure-changing operation (like passivization) is applied, we might end up with a different (structural) case

inherent case

is part of the lexical entry of a given predicate: idiosyncratic property; is assigned to an

argument together with theta role

- if a structure-changing operation (like passivization) is applied, inherent case is not affectes → lexical case cannot be changed

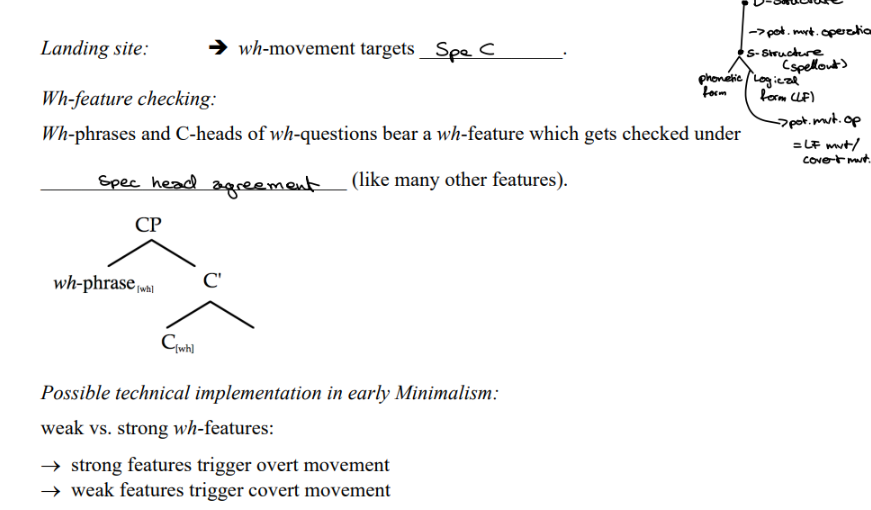
The Wh-Movement Parameter

Underlying assumptions:

The semantic interpretation of questions does not differ crosslinguistically.

Semantically speaking, wh-operators must take scope over the clause —>

syntactically speaking, wh-phrases must c-command the clause they take scope over

as a result wh- phrases must occur “in clause initial position SpecC at the latest

Crosslinguistic variation:

Languages can differ with respect to the point in the derivation when wh-movement takes

place —> overt movement vs. covert (= LF) movement

(parametric variation)

Platos Problem

• How can we know soth we have not been taught before?

• → applied to human language: puzzle of language acquisition (poverty of the stimulus)

  • By the age of 4-5 years (i.e. very quickly), children have acquired the grammar of their native language in a perfect way independent of their intelligence and social environment, and despite restricted and defective empirical evidence.

• Answer of generative grammar:

• We are endowed with a genetically encoded language faculty.

  → innate knowledge of language (Innateness Hypothesis)

If "language is innate", how can we account for the diversity of natural languages, i.e. crosslinguistic variation?

levels of adequacy

→ formulate syntactic rules that derive the structures we find

Levels of adequacy (cf. Chomsky 1965)

Observational Adequacy

• provide a description of the facts; characterization of the linguistic data

Descriptive Adequacy

• "A descriptively adequate grammar will not only describe the linguistic data, but itwill contain the general principles and processes that enable the native speaker toproduce and interpret sentences in his language and decide on the acceptability of sentences." (Haegeman 21994: 7)

• explicit formulation of a native speaker's internal grammar

• shift of focus from language to competence

Explanatory Adequacy

• explain observations

• "[A] theory reaches explanatory adequacy if it can account for the fact that the

  principles of the internal grammar can get to be known by the speaker, i.e. if it can account for language acquisition." (Haegeman 21994: 10)

• A theory achieves explanatory adequacy if it finds an answer to Plato's problem.

1970s/1980s:

• goal: achieve explanatory adequacy (i.e. find an answer to Plato's problem)

→ development of the Principles & Parameters Theory

Basic idea of P&P Theory

• Principles:

  • What is innate are rules, categories and operations which are common to all natural languages: universal principles that make up Universal Grammar (UG).

• Parameters:

  • These underlying universal principles are parametrized; i.e., they leave open certain options whose choice is determined by the linguistic data of a given language.

• A parameter can be compared to a "switch": UG provides the switch as such, and every language determines whether a given switch is on or off (parametrization).

• Children are therefore familiar with the switches (innate); they only have to find out on the basis of the input whether a given switch is on or off in their native language.

• Consequence:

  • On this assumption, grammar becomes flexible enough to account for crosslinguistic variation.

  • On the other hand, the set of rules a child has to acquire during language acquisition remains restricted enough to make sure it succeeds:

  → The universal principles are innate.

  → The parameters are set when the language is acquired on the basis of linguistic input.

  → best known version of a P&P theory: Government & Binding Theory

• Conclusion:

  P&P Theory è is the first theory of grammar that achieves explanatory adequacy,

  → i.e., it provides a good answer to Plato's problem!

Optimality Theory

Basic idea

Optimality Theory (OT) is a framework which is based on the assumption that rules are violable and ranked in a (language-specific) hierarchy. Thus, a grammatical form may violate a rule/constraint X if all alternative forms come off worse with respect to a higher-ranked (i.e. more important) constraint Y

Basic Terms and Notation of OT

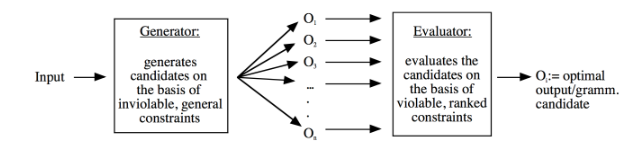
• input: "underlying scenario" (will become more specific in the linguistic examples)

• outputs (or output candidates): all kinds of possible solutions/potential winners → depends on the given input!

• (optimality-theoretic) competition, winners + losers:

  • All these candidates compete with each other.

  • The optimality-theoretic competition determines (usually) one optimal candidate, the winner.

  • All other candidates lose = are considered equally bad/equally ungrammatical.

• constraints, constraint hierarchy + constraint profiles:

  • The rules that determine the outcome of the competition are called constraints.

  • Constraints are violable, universal, and ranked in a hierarchy.

  • In order to win the competition, a candidate must have a better constraint profile than

  • all the competing candidates, i.e, it must satisfy the constraints 'better' than the other

  • candidates (even if it also violates some of the constraints).

• cumulativity:

  • Assume that constraint A is higher ranked than constraint B. Notation: A >> B. Assume further that candidate O1 violates A, and candidate O2 violates B. Then, obviously, O2comes off better than O1. Note that this result does not change even if O1 violates A only once, whereas O2 violates B several times!

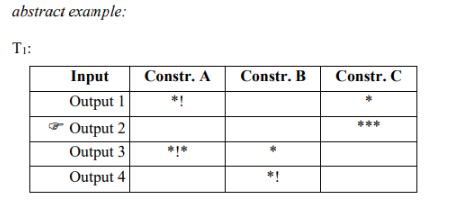
• tableaux:

  • OT-competitions are represented in tables that are called tableaux (sg. tableau).

  • Stars, *, indicate constraint violations.

  • Violations that make a candidate lose the competition are marked with an

    additional exclamation mark, *!, and are called fatal violations.

  • Tableaux reflect the underlying constraint hierarchy, since higher-ranked constraints occur to the left of lower-ranked constraints. Thus, it is easy to determine the optimal output in a given tableau: it is the candidate whose first star is the farthest to the right. (If there are two such candidates, the next lower constraint violation is decisive.)

  • The winner is usually marked with the symbol →

X harmonically bounds candidate Y (= Y is harmonically bounded by X) iff

1. here is no constraint a such that Y satisfies a better than X and

2. there is at least one constraint which X satisfies better than Y.

Consequence:

• Y can never be optimal, even if the constraints are reranked (= hierarchically ordered in a different way).

Crosslinguistic variation: in OT

The differences between languages are not captured by different constraints (recall that they are universal), but by reranking the constraints in different ways.

The inherent structure of an OT grammar

There are some very general principles for which it would not make sense if they were violable. Ex.: in syntax: for instance, general X'-scheme underlying syntactic structure etc.

→apart from the violable OT constraints, an OT grammar also consists of some very basic principles which are inviolable and make up the rough framework; this part of the OT grammar is called Generator = Gen.

Conflicts in Grammar

Rules in grammar:

They are motivated on the basis of empirical data; however, sometimes they stand in conflict

with each other.

Possible solutions in traditional grammar models: one of the rules must be abandoned, or there

must be exceptions to the rule, or they do not apply universally/at all levels

Solution in an OT grammar: both rules are valid, but they are violable and ranked → we know the winner in advance, we are trying to find a predictng analysis

Repair Phenomena

Certain grammatical data exhibit properties which are normally not tolerated in grammar; they seem to serve as a "last resort" if all alternatives are even worse.

In (4-c)/(4-d) an additional him occurs —> resumptive pronoun

The insertion of this resumptive pronoun is only allowed in (4-d); the operation seems to be a repair phenomenon, a last resort, since there is no grammatical alternative (cf. (4-b), which violates the Complex NP Constraint).

Assumption: resumptive pronouns are not part of the input; they are inserted as a last resort to 'save' the structure. (Note: otherwise (4-a)/(4-c) and (4-b)/(4-d) would not be candidates in the same competition!)

Why are last resort strategies problematic for other theories of grammar?

It is not trivial to explain why certain constructions are only allowed if alternative structures are ruled out (cf. resumptive pronoun insertion: why is it possible in (4-d) but not in (4-c)?)

→ Last resort phenomena seem to rely on the assumption that the grammaticality of a structure depends on the properties of competing structures. This is one of the basic concepts of OT!

The Emergence of the Unmarked

• Empirical data suggest that there is often a default case (or 'elsewhere case'), which means that a certain property or form is the unmarked case which surfaces whenever no other more specific form is required. In traditional grammars it is difficult to capture this phenomenon; in an OT grammar this can be accounted for straightforwardly:

• "Emergence of the umarked": results if a low-ranked constraint becomes decisive which is always present but usually overriden by higher-ranked constraints which require something else (cf. also the "365years"-constraint from the first handout).

• Example: Case assignment in German

  default Case in German: Nominative Case; i.e., if there are no other explicit requirements, a German DP gets Nominative Case

• Nominative Case is not allowed in contexts in which other Cases are explicitly required: Example for explicit Case requirement (simplified): The object DP of a transitive verb bears Accusative Case.

• Why is the default Case problematic for other theories of grammar?

  ssumption in GB-theory (simplified): A DP is assigned Nominative Case in SpecT if the corresponding T is finite (= 'Nominative Case assignment by finite T under Spec-head agreement'). Note moreover that every overt DP must be Case-marked (= principle called Case Filter.)

Constraint ties

Optionality

• Since identical constraint profiles are not very likely to occur, tied constraints provide a much better account of optionality.

Global ties:

• Informally, a tie can be explained as follows: If two constraints X and Y are tied, a violation of X is as serious as a violation of Y. Notation: X ◦ Y

• A constraint hierarchy with the global tie X ◦ Y stands for two separate hierarchies, one of them containing the dominance relation X ≫ Y, the other one containing the relation Y ≫ X

Consequences:

• If O1 satisfies X better than O2 but violates Y more often than O2 and they behave alike with respect to higher-ranked constraints, but all the other candidates come off worse, then both O1 and O2 are optimal – O1 wins the competition with the underlying constraint order α, O2 wins with the underlying constraint order β; cf. T1 and T2.

Priciple A

An anaphor must be bound in its binding domain

include reflexives (like myself, yourself, himself) and reciprocals (each other)

Principle B

Pronoun must be free in its binding domain

Principle C

An expression must be free

Binding domain

• If a bears Nominative Case, its binding domain is the smallest XP containing a.

• Otherwise, a's binding domain is the smallest XP containing a and a subject (≠ a and which does not contain a).

• rule of thumb to determine the BD:

  • starting at node a and going up the tree, where is the next subject? BD = the first node you reach that contains this subject. Note: subject traces also count!!! a itself only counts if it bears Nominative Case.

Some Problems for BT

• Principle A and B suggest that pronouns and anaphors are always in complementary distribution; however, there are examples where this is not the case (in English as well as in other languages): optionality can arise!

• In many languages two different types of anaphors can be observed which differ with respect to their distribution. Principle A cannot account for these facts; it treats all anaphors alike.

• Principle A suggests that anaphoric binding is a very local phenomenon; however, in some language (like Icelandic) anaphors may be bound across longer distances ("long distance binding")

• Even in more local binding relations, we can observe a wide range of crosslinguistic variation. How can this be accounted for?

Universal Tendencies and Crosslinguistic Variation

of Anaphors and pronouns

Similarities across languages

• Bound Element:

  • Gradually shifts from SELF anaphor to SE anaphor to pronoun

  • optionality btw SELF/SE and SE/pron might arise

• Distance: the distance btw antecdent and bound elemt increases

Crosslinguistic Variation

• English lacks SE anaphors

• The realization of the bound element in the same syntactic context might differ

• The exact point when the realization changes from SELF anaphor to SE anaphor to pronoun might differ.

• The size of the domains (i.e. the degree of locality) when the realization form changes from SELF to SE anaphor and from SE anaphor to pronoun can vary.

• Whether optionality occurs at all and in which domains also depends on the language under consideration.

Universal tendencies

• If the binding relation is very local, the bound element surfaces as complex anaphor; if it is slightly less local, it surfaces as simple anaphor (if it exists in the given language); in non-local binding relations, the bound element surfaces as pronoun. In the "transition zones" (from SELF to SE anaphor and from SE anaphor to pronoun), optionality might arise

General patterns of binding Data

• If anaphoric binding is licit in domain D1, it is also licit in domain D2, if D2 is smaller than D1.

• If pronominal binding is licit in domain D1, it is also licit in domain D2, if D2 is bigger than D1.

• As the distance between antecedent and bound element increases, the realization form of the bound element changes from SELF anaphor to SE anaphor and then to pronoun.

• Optionality between SELF anaphors and pronouns cannot arise if SE anaphors are also available.

Binding sensitive domains

There is not just one binding domain to which binding relations are sensitive (as in standard Binding Theory); instead, binding is sensitive to several domains of different size.

Ranking: theta > case > subject> finite > indicative > root

This pattern follows straightforwardly from the generalization in (6-a) if it is assumed that the type of domain in which binding takes place gets bigger when we replace an infinitival with a subjunctive complement clause or a subjunctive with an indicative complement clause.

Consequence:

LD binding = binding in a domain > subject domain

Since we find three different patterns of LD binding (= binding outside of the subject domain), we should differentiate three different domains bigger than the subject domain, not just one (i.e. the root domain):

Theta Domains

Of a is the smallest XP conatining the had that theta marks a plus its argument positions

Case domain

The case domain of a is the samllest XP conaining a and the head that case marks a

Subject domain

Of a is the smallest XP conating a and a subject distinct from a

Root domain

Of a is the XP that forms the root of the sentence conatining a

Smallest binding domains to languages

Long distance binding

The bound element is embedded in a complement clause, its antecedent is part of the embedding clause; LD binding generally refers to anaphoric binding in such a context.

Observation:

Languages that allow anaphoric binding across clause boundaries do not necessarily allow it in all syntactic contexts alike:

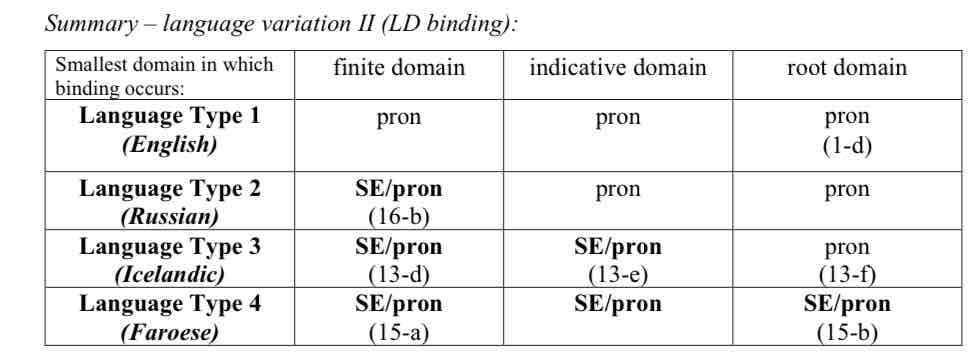
• Icelandic allows LD binding into infinitival and subjunctive clauses (cf. (13-d), (13-e)), but not into indicative clauses (cf. (13-f)).

• It is therefore not the case that a language either generally allows LD binding or not; the system is more fine-grained.

Underlying pattern:

• LD binding occurs most likely into infinitival complements, and least likely into indicative complements.

• If a language can have LD reflexives in subjunctive complements, they are also licit in infinitival complements, and

• if LD reflexives can occur in indicative complements, they are also licit in subjunctive complements (cf. Burzio 1998, Fischer 2004).

Crosslinguistic variation with respect to LD binding:

• L1: LD binding generally ruled out (E, Ger)

• L2: LD binding is only allowed into infinitival comp clauses (russian)

• L3: LDB is allowed into infinitival and subjunctive comp. Clauses (icelandic)

• L4: LDB is allowed into infinitival sunjunctive and indicative comp clauses (faroese)

Finite domain

Smallest XP containing a and a finite verb

Indicative domain

Smallest XP that conatins a and an indicative verb

Observation of verb forms

• Embedded verb of infinitival complement: non finite, non indicative

• embedded verb of subjunctive complement: finite, non indicative

• embedded verb of indicative complement: finite, indicative

• matrix verb: finite indicative

→ indicative verb is also finite (but NOt vice versa)

Smallest binding domains VD

Principle C as a violable constraint

Observation

In some languages, even violations of Principle C seem to be licit. (Note however that even in these languages, R-expressions may never be bound by pronouns.)

Note:

An OT approach could account for this straightforwardly by ranking the constraint that is responsible for Principle C violations relatively high in languages like English, but lower in languages like Vietnamese. (That R-expressions may universally not be bound by pronouns also follows straightforwardly from the OT analysis we will discuss.)

Binding in a local derivational approach

Goals:

Empirically: Capture binding data

Conceptually: develop binding theory

• that adopts derivational view of syntax (tree built from bottom up) and

• In which, in addition the accessible domain is restricted → compitability with Phase impenetrability condition (PIC)

Why does this require some effort?

• binding not strictly local phenomenon: antecedent & bound element can be separated by phase boundaries (LD pinding, pronominal binding)

• On the other hand, the concrete distance between antecedent and bound element is crucial: it determines the realization of the bound element as SELF anaphor, SE anaphor, or pronoun.

→ Hence, the solution cannot just be to split up the non-local relation into several local ones, as it is done, for instance, in the case of successive-cyclic wh-movement.

Matrix Model

How to account for optionality and crosslinguistic variation

PIc compatibility

How to account for optionality and crosslinguistic variation:

This remains largely unanswered in many other theories of binding.

Our answer: an OT analysis ® constraint ties + reranking!

The underlying principles can be formulated in such a general way that they reflect the universal tendencies, while violable constraints plus reranking keep the system flexible enough to account for all the language-specific differences.

PIC-compatibility:

(i) In order to evaluate a binding relation, we need to know the exact configuration that holds between the bound element (= x) and its antecedent.

However, the surface position of x might no longer be accessible when the binder is merged into the derivation.

→ We have to make sure that x is dragged along until both elements are accessible at the same time.

→ Then, binding is licensed (via feature checking of the binding feature b; the need to check this feature motivates movement of x).

On the assumption that every phrase is a phase, the configuration in which the binding relation is licensed looks as seen in picture

Matrix Model underlying assumptions: narrow syntax- how to determine bindee

• The bound element x starts out as a variable equipped with a "realization matrix", i.e., a list which contains all possible realizations of x (as SELF anaphor, SE anaphor, pronoun).

  → maximal realization matrix =: [SELF, SE, pron]

• Each time x reaches one of the binding-sensitive domains and x remains unbound, its realization matrix might be reduced → the most anaphoric realization might be deleted and henceforth no longer be available (depending on the respective domain and the language under consideration).

• x stops moving when it can establish a checking relation with its antecedent; at this stage, its concrete realization can be determined, which must match one of the remaining forms in the realization matrix.

PART II: Post-syntactic operations in Matrix Model

Determining the concrete realization of x: if there is only one element left in the realization matrix, the choice is clear, otherwise the remaining form that is most anaphoric is selected. This operation takes place at PF.

Once the form of x is known, the whole chain it heads can be aligned and x can then be spelled out in the appropriate position. This kind of reference to earlier parts of the derivation is strictly restricted to items that have some connection to the current stage of the derivation via chain formation, and the only thing that happens is that the lower chain members are specified more precisely in accordance with the predispositions they already had before.

Domains, Constraints, and Candidates basic assmptions

First input:

• The optimal realization of a bound element x is determined in an optimality-theoretic competition in the course of the derivation; in the input it is only encoded that there will be a binding relation between the designated antecedent and x (plus numeration or the like); e.g. {Max[b], hates, x[b]} for Max1 hates himself1.

Local optimization:

• Optimization takes place after the completion of each phrase. The optimal output of a competition serves as input for the next optimization process (cf. Heck & Müller 2000 and subsequent work on derivational OT syntax).

Binding domains:

• It is assumed that binding is sensitive to domains of different size (cf. (2)-(7)).

Constraints:

• There is a group of constraints that refer to these domains and favor one type of realization; they are ordered in a universal subhierarchy.

• Another group of constraints favors the other extreme; these constraints are also ordered in a universal subhierarchy.

Reranking:

• Different interaction between these two universal subhierarchies accounts for crosslinguistic differences, while the observed universal properties can still be captured due to the relative restriciveness of the system.

Candidates:

• The competing candidates differ from each other with respect to the realization matrix of x: at each step, it is possible to reduce the matrix by deleting anaphoric elements. In the beginning, we start with the maximal realization matrix, i.e., in the first competition we have three candidates:

  • [SELF; SE, pron]

  • [SE, pron]

  • [pron]

MAtrix Model binding sensitive domains

• XP Domain (XP): XP is a phrase conatining X

• ThD: XP is the ThD of x if it contains x and the head that theta marks x plus its external argument (if there is one)

• Case domain (CD): XP is the Case domain of x if it contains x and the head that bears the Case features against which x checks Case.

• Subject domain (SD): XP is the subject domain of x if it contains x and either

  • a subject distinct from x which does not contain x, or

  • the T with which x checks its (Nominative) Case features.

• Finite domain (FD): XP is the finite domain of x if it contains x, a finite verb and a subject.

• Indicative domain (ID): XP is the indicative domain of x if it contains x, an indicative verb and a subject

They require that x be minimally anaphoric if binding has not yet taken place in XD (XD Î {any XP (XP), ThD, CD, SD, FD, ID}

Principle A constraints

PRINCIPLE AXD (PR. AXD):

If x[b] remains unchecked in its XD, x must be minimally anaphoric.

If the derivation reaches one of the relevant domains and no binding relation is established, these constraints apply non-vacuously and are violated twice by candidate O1 (which contains two anaphoric specifications, SELF and SE), once by O2 (which contains one anaphoric specification, SE), and not at all by O3 (which only contains the pronominal specification)

Faith constraints

They must function as counterbalance to the PRINCIPLE A-constraints; hence, they must be ordered in such a way that they favor anaphoric specifications.

• FAITHSELF (FSELF): The realization matrix of x must contain [SELF].

• FAITHSE (FSE): The realization matrix of x must contain [SE].

• FAITHpron (Fpron): The realization matrix of x must contain [pron].

Universal subhierarchy

• FAITHpron >> FAITHSE >> FAITHSELF

The realization of x:

• Strictly speaking, the FAITH-constraints do not yet say anything about the concrete realization of x; (11) only favors O1, which contains the maximal realization matrix and therefore violates none of the FAITH-constraints.

Maximally anaphoric binding

Assumption:

Once x is bound, the most anaphoric element of the optimal specification matrix is selected

MAXIMALLY ANAPHORIC BINDING (MAB) (not violable):

Checked beta features (x[b]) must be realized maximally anaphorically.

• optimal matrix = [SELF, SE, pron] → MAB-prediction: realization as SELF anaphor

• optimal matrix = [SE, pron] → MAB-prediction: realization as SE anaphor

• optimal matrix = [pron] → MAB-prediction: realization as pronoun