3.4-3.6 searching, sorting and optimisation algorithms

linear search algorithm

each item on an array is inspected in turn until the desired item is found

characteristics of the linear search algorithm

-does not need an ordered array

-simple, easy to program

-inefficient, high time complexity of O(n)

-cannot tell if the desired item is not in the array until it is fully searched

-best used on small data sets

binary search algorithm

-the midpoint of an array is inspected (if the array contains an even number of items the midpoint is the latter of the two middle items)

-if it is the desired item the algorithm completes

-if it is not the desired item it is compared alphabetically with it, and the half of the array(including the midpoint) that could not contain the desired term is discarded

-this repeats until the desired term is found or the array is empty

characteristics of the binary search algorithm

-can only be used on ordered arrays

-complex, difficult to program

-efficient, low time complexity of O(logn)

-best used on larger data sets

binary tree search algorithm

a binary search conducted on a binary tree

bubble sort algorithm

-adjacent items in the array are checked and swapped if they are not in order, going from the beginning to the end of the array

-this repeats until the array has been passed through without the need to make any swaps

characteristics of the bubble sort algorithm

-inefficient, high time complexity of O(n^2)

-simple, easy to program

-best used on small data sets

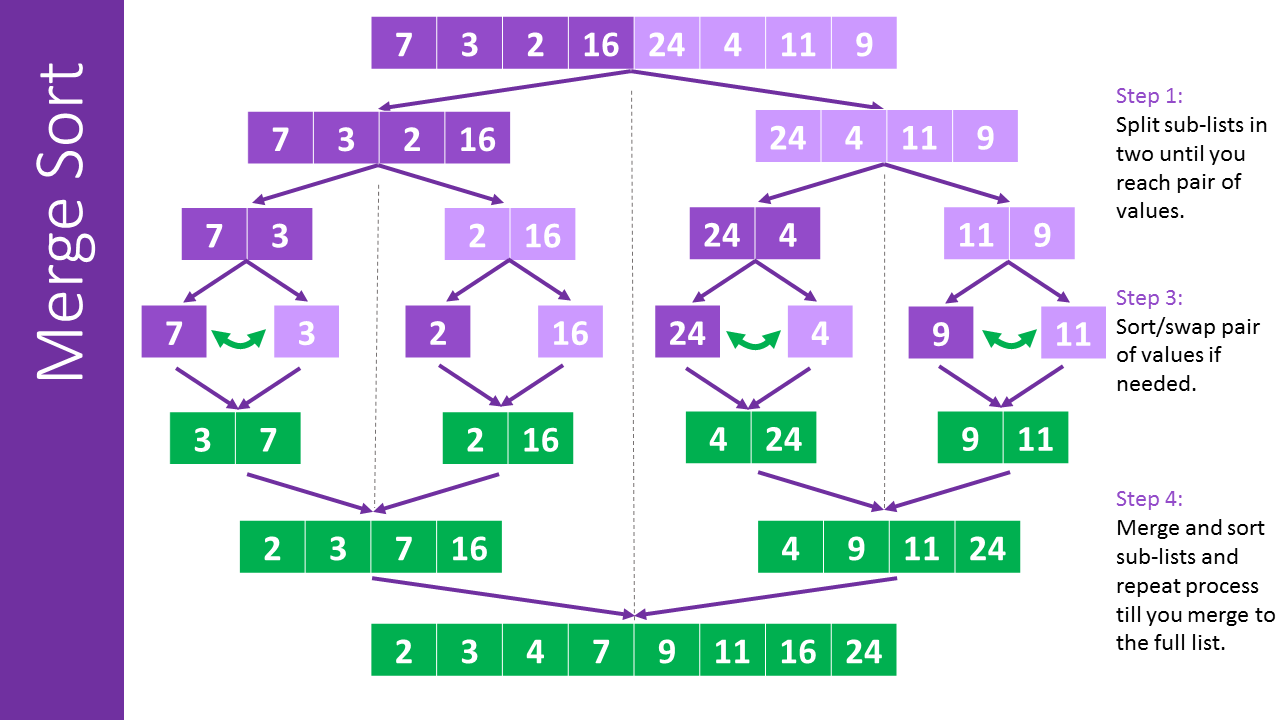
merge sort algorithm

-the array is split into two sub-arrays

-the sub-arrays are split continuously until each sub-array consists of only one item

-pairs of sub-arrays are then merged back together in order, comparing the first item in each and adding the first of the two to the merged array until only one item remains, which is appended to the end of the merged array

-this repeats until there is only one array

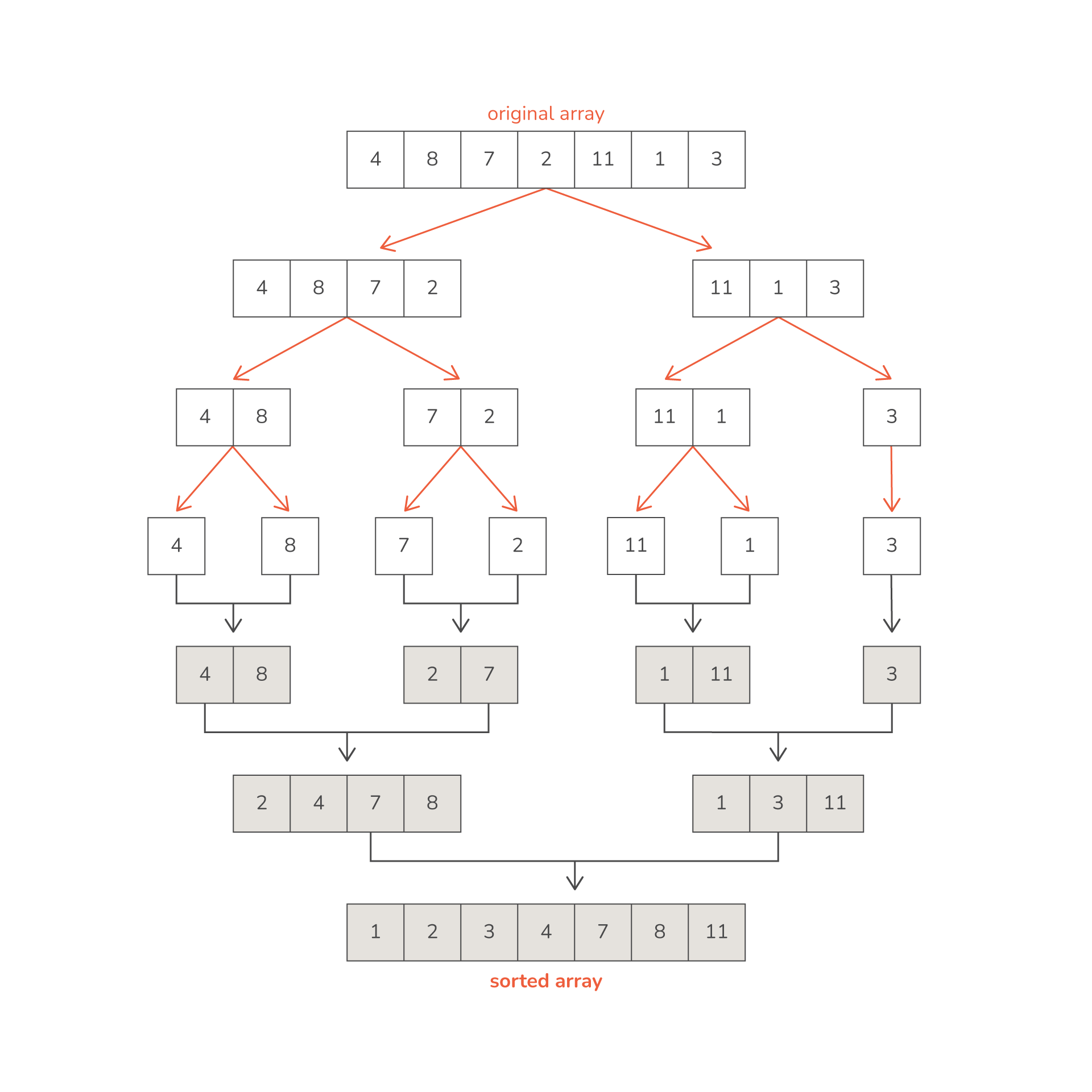
merge sort algorithm with a non base-2 number of terms

if the parent array contains an odd number of items the middle item is included in the first sub-array

when a 3 item sub-array splits further the first two items form one sub-array and the third forms the other by itself and nothing happens to it over the next step while the 2 item sub-arrays split further

when 3 single-item sub-arrays recombine, the two on the left combine first while nothing happens to the third item, then both sub-arrays recombine as normal)

(middle items can be implemented into either sub-array depending on the algorithm used, but I am using this as an example)

characteristics of the merge sort algorithm

-efficient, time complexity of O(nlogn)

-complex, difficult to program

-best used on larger data sets

optimisation algorithms

algorithms designed to find the best possible solution to a problem

dijkstra's shortest-path algorithm

an algorithm that finds the shortest path from a starting node to every other node on a weighted graph

tracing dijkstra's shortest-path algorithm

-start and end nodes are selected and their distance from the start node is noted

(all nodes have an arbitrarily large value as their distance from the start node, signifying there being no path, until it is updated, except for the start node whose distance to itself is 0)

-the distance between the start node and all adjacent nodes are updated. the start node is now fully explored

-the unexplored node with the lowest distance is explored next

-the distance to the start node through the currently explored node is calculated for all adjacent nodes(equal to the CEN's distance to the SN, plus its distance to the AN), and updated if it is lower than the current distance for that node

-the previous 2 steps continue until all nodes are fully explored

uses of dijkstra's shortest-path algorithm

-navigation systems

-routers sending packets across a network