ap stats unit 1 notes

quantitative data

data that is numerical. the values have an inherent order. examples: income, weight, height # of classes

*can you average the data? YES

categorical data

datat where values are categories or group labels, which often don’t have an inherent order. examples: eye color, relationship status, left or right

*cannot be averaged

misleading graphs may not have axis labels or ___

scale

misleading graphs may __ the x or y axis, or start at a weird place

cut off

misleading graphs may use __ for a bar graph also called what

pictures, also called a pictograph

mean formula

_{sum of all values / number of all values}

median

middle

if it’s odd, use middle value of data set, if even use the value in between

approximating a median in a histogram

1. label the frequency

2. add up the frequency

3. divide by two

4. find the bins that contain the median, the nth data point

formula for range

range = max - min

why do you think we find the difference between each data point and the mean, standard deviation (Sx) is a measure of spread

it’s a way to measure distance between data values and the mean

Formula of interquartile range (IQR)

Q3 - Q1

resistance

not seriously affected by

Is the median resistant by skew and outliers

yes, the ___ is resistance by skews and outliers (median/mean)

Is the mean resistance to skews and outliers

No, the ___ is NOT resistance by skews and outliers (median/mean)

is the IQR resistant to skews and outlers?

Yes, the ___ is resistant to skews and outliers. (IQR/range and standard deviation)

Is range and standard deviation resistant to outliers

No, the ___ is NOT resistant to skews and outliers (IQR/range and standard deviation)

Why is the mean not resistant to skews and outliers

The mean can drag up or drag down values in calculation

Why is the median and IQR resistant to skews and outliers

Position matters more than the value, the outlier is not given a large weight in calculation

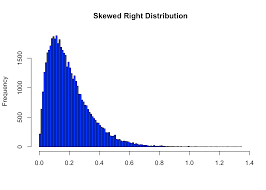
Right skew

mean > median

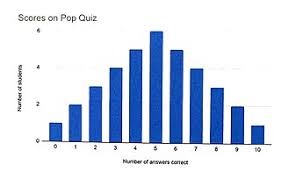
symmetric

mean = median

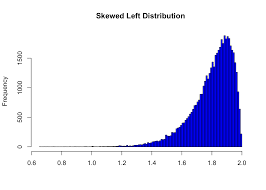
left skew

mean < median

Advantages to using a dotplot to visualize data

see every data point

Disadvantages to using a dotplot to visualize data

• can’t always see exact value

• not great for large data sets

Advantages to using a stemplot to visualize data

See exact values

Disadvantages to using a stemplot to visualize data

not great for large data sets

Advantages to using a histogram to visualize data

Great for large data sets

Disadvantages to using a histogram to visualize data

Can’t see individual values

when asked to describe the distribution use …

CSOCS

1st C in CSOCS

Context: what variable is being measured. Example: The distribution of payroll for 2002 baseball teams…

1st S in CSOCS

Shape: right/left skew, symmetric modes (unimodal or bimodal)

O in CSOCS

Outliers: unusual points. Examples: No obvious outliers

2nd C in CSOCS

Center: mean, median, general center. Example: The center is approximately $50 million

2nd S in CSOCS

Spread: range, IQR, standard deviation. Example: Has a range of between $20-140 million

outliers

unusually high or low data values

Formulas for outlier boundaries

Upper Limit and Lower Limit

Upper limit

Q3 + 1.5 x IQR

Lower Limit

Q1 - 1.5 x IQR

CSOCS for boxplot

• Context: subject of data

• Shape: Skew (not modes) shape may not be determined

• Outlier: dots/astriecks

• Center: median

• Spread: IQR

Comparing distirbutions

Use CSOCS and use comparative language for each feature, use AND, not but or howeve.

Percentile

percent of data less than or equal to a certain data value

standardization

a point’s location in the distribution depends on both distance from the center and the distribution’s spread (or variability)

formula for z score

z = (x - mean) / Standard deviation (sx)

If data value > mean

positive z-score

if data value < mean

negative z score

positive z score

the number of standard deviation, ABOVE THE MEAN

negative z score

the number of standard deviations, BELOW the mean

The normal curve

• symmetric

• mean = median, both located at center

The empirical rule

normal curves 1,2,3 standard deviations away from the mean

Empirical rule: 1 SD from mean

68%

Empirical rule: 2 SD from mean

95%

Empirical rule: 3 SD from mean

99.7%

strategy for normal curves

• draw + label curve

• perform calculations

• answer the question with context

Empirical rule: 3 SD from the mean is statistically significant how

Out of the norm

Percentile will always be shaded to the…

to the left

Empirical rule FORMULA: 1 SD from mean

Mean ± 1(Standard deviation)

Empirical rule FORMULA: 2 SD from mean

Mean ± 2(Standard deviation)

Empirical rule FORMULA: 3 SD from mean

Mean ± 3(Standard deviation)