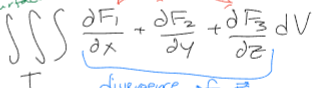Triple Integrals

Volume

∫∫∫_SdV

Average Value

1/V * ∫∫∫_Sf(x,y,z) dV

Mass of solid with density

∫∫∫_Sδ(x,y,z) dV

centroid of a solid

x_A = (∫∫∫_S x dV) / V; repeat for y and z

Center of Mass with density

x_M = (∫∫∫_S xδ(x,y,z) dV) / M

Moment of Inertia

relationship between angular acceleration and torque; mass/velocity * ∫∫∫(distance to axis)² dV

triple integrals geometrically

“adding up” a function over every point in a solid

Volume of a Solid bounds

outside integral → constant; middle bounds → only include remaining variable; inside integral → can include two other variables

how do you find bounds (upper/lower)?

plug in point with the two variable coordinates (not the variable you’re finding the bounds for) that is inside the intersection

Flux Integral

integral of a vector field over a surface; flow of a vector field through a surface calculated by F * N

Spiral/Helix parameterization

<cost, sint, 0.1t>

Line parameterization

<2-t, 1+3t, 4t> = <2, 1, 0> + t <-1, 3, 4>

Torus/Donut parameterization

<(b+acos(s))cost, (b + cos(s))sint, asin(s)>

Cylinder parameterization

<cost, sint, s>

Describe surfaces

use parametric equation with 2 variables; partial derivatives get tangent vectors; cross-product of two partial derivatives get normal vector; calculate surface area by double integrating normal vector’s length

normal vector of r(u,v)

r_u(u,v) x r_v(u,v)

Surface area equation

∫∫∫_D l r_u(u,v) x r_v(u,v) l dudv

Flux of a vector field F through a parameterized surface r(u,v)

∫∫_DF * N dA; dot product of vector field and normal vector of parameterized surface

Calculate Flux Process

1- parameterize; 2- plug parameterization into vector field; 3- calculate N = r_u x r_v; 4- dot product of 2 & 3; 5- integrate (double)

Divergence Theorem

If T is a solid bounded inside the closed surface S, to calculate the flux of a vector field through S, then

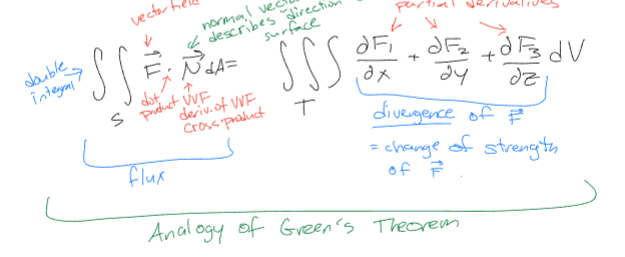
Divergence Theorem Equation

∫∫∫_T dF₁/dx + dF₂/dy + dF₃/dz dV