Remade Final Exam Memorization

New from 12/1

Rewrite a^n = b as a logarithm

\log_{a}{b} = n

Rewrite \ln(a) in log form

\log_{e}{a}

Product/Quotient Rule for Logarithms

• \log_{b}{(M \cdot N)} = \log_{b}{M} + \log_{b}{N}

• \ln{(M \cdot N)} = \ln{M} + \ln{N}

• If Quotient: Replace \cdot \to \div and + \to -

Power Rule for Logarithms

• \log_{b}{M^k} = k \cdot \log_{b}{M}

• \ln{M^k} = k \cdot \ln{M}

Logarithm of the Base Rule:

• \log_{b}{b} = 1

• \log{10} = 1

• \ln{e} = 1

• \ln(1) = 0

Inverse Logarithm of the Base Rule (for ln):

• e^{\ln{a}} = a

• \ln{e^x} = x

Power Rule of integration: \int x^n =

\frac{x^{n+1}}{n+1} + C

Integral of Constants \int n =

nx + C

Integral of e^{ax}

\frac{1}{a} e^{ax} + C

Integral of a^x

\frac{a^x}{\ln(a)} + C

Integral of 1/x

\ln |x| + C

integral of cos x

sin x + C

Integral of sin x

-cos x + C

integral of sec²x

tan x + C

integral of csc²x

-cot x +C

What is the Integration trick

• sec sec tan

• -csc csc cot

integral of tan x sec x

sec x + C

integral of cot x csc x

-csc x +C

Integral of \frac{1}{\sqrt{1-x²}}

arcsin x

Integral of - \frac{1}{\sqrt{1-x²}}

arc cos x + C

Integral of \frac{1}{1 + x²}

arctan x + C

Integral of -\frac{1}{1 + x²}

arccot x + C

Integral of \frac{1}{x\sqrt{x² - 1}}

arcsec x + C

Integral of -\frac{1}{x\sqrt{x² - 1}}

arccsc x + C

Double Angle Identity for \sin(2x)

2\sin(x)\cos(x)

Double Angle Identity for \cos(2x)

1. \cos^2(x) - \sin^2(x)

2. 1 - 2\sin^2(x)

3. 2\cos^2(x) - 1

Double Angle Identity for \tan(2x)

\frac{2\tan(x)}{1 - \tan^2(x)}

Power Reduction Half Angle Identity for \sin²(x)

-\frac{1}{2} + \frac{\cos(2x)}{2}

Power Reduction Half Angle Identity for \cos²(x)

\frac{1}{2} + \frac{\cos(2x)}{2}

Pythagorean Identity for sin and cos

\sin²x + \cos²x = 1

Pythagorean Identity for tan and sec

1 + \tan²x = \sec²x

Integral of tan(x)

\ln|\sec(x)| \quad \text{or} \quad -\ln|\cos(x)|

Integral of csc(x)

\ln|\csc(x) - \cot(x)| \quad \text{or} \quad -\ln|\csc(x) + \cot(x)|

Integral of sec(x)

\ln|\sec(x) + \tan(x)|

Integral of cot(x)

\ln|\sin(x)|

d/dx sin(x)

cos(x)

d/dx cos(x)

-sin(x)

d/dx tan(x)

sec²(x)

d/dx cot(x)

-csc²(x)

d/dx sec(x)

sec(x) tan(x)

d/dx csc(x)

-csc(x) cot(x)

d/dx arcsin(x)

\frac{1}{\sqrt{1-x²}}

d/dx arccos(x)

-\frac{1}{\sqrt{1-x²}}

d/dx arctan(x)

\frac{1}{1+x²}

d/dx arccot(x)

-\frac{1}{1+x²}

d/dx arcsec(x)

\frac{1}{x\sqrt{x²-1}}

d/dx arccsc(x)

-\frac{1}{x\sqrt{x²-1}}

Formula for finding the vertex of an equation with degree of 2

x = -\frac{b}{2a} where function in form of ax² + bx + c

Given coordinates of the tail and the head of a 2D vector, find the position vector using <> notation

<x_2 - x_1, y_2 - y_1>

What is a position vector?

Vectors that have a head starting at (0,0) or (0,0,0)

Midpoint formula for a vector given two points A(x_1, y_1, z_1) \text{ and } B(x_2, y_2, z_2)
What is this useful for?

M=(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}, \frac{z_1+z_2}{2})
Useful for finding equation of a sphere passing through A and B with center at midpoint of \vec{AB}

3D Sphere Standard Form Equation

(x-a)²+(y-b)²+(z-c)²=r² for center (a,b,c)

Completing the square formula

(\frac{b}{2})²

Unit Vector Definition & Formula

• Vector with length / magnitude of 1

• Formula: \frac{\overrightarrow{v}}{|\overrightarrow{v}|}

1. Colinear is when

2. Colinear Formula (For Points P,Q,R)

3. Two 3D Vectors are Colinear if

1. Three or more points lie along one straight line

2. \overrightarrow{PQ} || k \cdot \overrightarrow{PR}

3. Their Cross Product is a Zero Vector

What is a force vector and how is it calculated?

A force vector is a vector \overrightarrow{u} multiplied by the force on that vector where \overrightarrow{u} is a unit vector

1. Find the vector’s magnitude

2. Find that vector’s unit vector (\hat{v} = \frac{\overrightarrow{v}}{|\overrightarrow{v}|} )

3. Multiply the unit vector by the force using scalar multiplication

Given Three Points that are vertices on a parallelogram, how do you validate if the fourth point completes the parallelogram?

1. Given Three points A, B, C, form three vectors of \overrightarrow{AB}, \overrightarrow{AC}, \overrightarrow{BC}

2. For each potential answer calculate the vector relationship of: \overrightarrow{AB} = \overrightarrow{CD}, \overrightarrow{AC} = \overrightarrow{BD}, \overrightarrow{BC} = \overrightarrow{AD}

   1. Notice like numbers and choose the right vector accordingly

3. If the vector relationship is equal, that point satisfies the parallelogram

Dot Products are useful for

1. Finding the angle between two vectors

2. Vector Projection

3. If dot product of two vectors is 0, vectors are perpendicular (orthogonal)

4. Normalizing Vectors

Geometric Dot Product Formula \overrightarrow{A} \cdot \overrightarrow{B} =

\overrightarrow{a} \cdot \overrightarrow{b} = |\overrightarrow{A}| |\overrightarrow{B}| \cos(\theta) (Use for projection)

Algebraic Dot Product Formula \overrightarrow{A} \cdot \overrightarrow{B} =

A_x B_x + A_y B_y + A_z B_z (Use for angle determination)

Angle Between Two Vectors Formua \theta =

\cos^{-1} \left( \frac{\vec{A} \cdot \vec{B}}{|\vec{A}| |\vec{B}|} \right) (uses non-geometric = geometric dot product formulas)

Cross Products are useful for

1. Result is normal vector: vector perpendicular to both input vectors

2. If result = 0 vector, input vectors are colinear and parallel

3. Area of a parallelogram = a \times b

4. Area of a parallelepiped = | \vec{A} \cdot (\vec{B} \times \vec{C}) |

Geometric Cross Product Formula |\vec{u} \times \vec{v}| =

|\overrightarrow{u} \times \overrightarrow{v}| = |\overrightarrow{u}| |\overrightarrow{v}| \sin(\theta)

Algebraic Vector Cross Product Formula (2D & 3D) \vec{A} \times \vec{B} =

• A_x B_y - A_y B_x (Scalar Result)

• Use the matrix (See Image) —> i |i_{\text{matrix}}| - j |j_{\text{matrix}}| + k |k_{\text{matrix}}| (Vector Result)

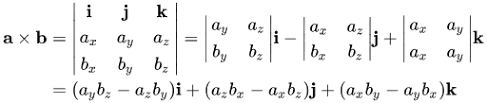
Area between two curves formula

• \int_{a}^{b} [f(x) - g(x)] dx where f(x) is to the right of g(x)

• \int_{c}^{d} [f(y) - g(y)] dy where f(y) is above g(y)

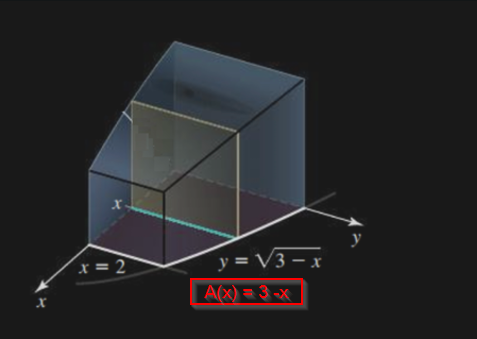
General Slicing Method Concept & Formula

• To find the volume of 3D solids, integrate the areas of cross-sectional slices perpendicular to a given rotational axis (see image)

• V = \int_{a}^{b} A(x) dx where A(x) is the area of the cross section at a given x coordinate

Washer Method Formula & Usage

• Around x-axis: \pi \cdot \int_{a}^{b} [R(x)² - r(x)²] dx

• Around y-axis: \pi \cdot \int_{c}^{d} [R(y)² - r(y)²] dY

Shell Method Formula & Usage

2\pi \int_{a}^{b} x \cdot f(x) \, dx

• Use when: f(x) & revolve y (f(y) revolve x)

Surface Area Formula

2\pi \int_{a}^{b} [(\text{radius} \cdot (\text{arc length}))] dx

• Where radius is usually f(x) (or x if in dy)

• And arc length = \sqrt{1 + f’(x)²}

Work Concepts & Formula

• Concept: Work is force * distance

• Formula: w = \int_a^b f(x) dx

  • a represents the starting distance (usually 0 meters)

  • b represents the ending distance (> 0 m)

  • f(x) is force as a function of distance, where x is the distance

Trig Substitution rules of thumb for sin(x) and cos(x):
- if one power is odd & other is even
- if both powers are even

1. Do u = sin(x) or u = cos(x) for the trig function with an even degree

2. Use half angle identities when both powers are even

   1. sin²x = -\frac{1}{2} + \frac{\cos{(2x)}}{2}

   2. cos²x = \frac{1}{2} + \frac{\cos{(2x)}}{2}

Trig Substitution rules of thumb for tan(x) and sec(x):
- If degree of sec is even
- If degree of tan is odd

1. If degree of secant is even do u = tan(x)

2. If degree of tan is odd use u = sec(x)

Trig Substitution rules of thumb for cot(x) and csc(x):
- If degree of csc is even
- If degree of cot is odd

1. If degree of csc is even use u = cot(x)

2. If degree of cot is odd, use u = csc(x)

What is LIATE Abbreviation and what is it used for

• Abbreviation for Logarithm, Inverse Trig, Algebra, Trig, and Exponential

• Used in integration by parts

Integration by parts formula

\int u dv = uv - \int v du

• Where in any problem set u using LIATE

• And dv to be whatever isn’t selected by LIATE

Steps to solving partial fraction questions

1. The degree of the denominator MUST be greater than the degree of the numerator. You can long divide to achieve this.

2. Factor out the denominator to get the lowest degrees possible

   1. Something like: \frac{…}{(x²+a)(x+5)(x-2)}

3. For Linear Factors (Degree of 1) use:

   1. \frac{…}{x-a} \rightarrow \frac{A}{x-a}

4. For Repeating Linear Factors (Degree of 1 and k) use:

   1. \frac{…}{(x \pm a)^k} = \frac{A_1}{(x-a)^1} + \frac{A_2}{(x-a)²} + … + \frac{A_k}{(x-a)^k}

5. For Irreducible Quadratics (Degree of 2) use:

   1. \frac{…}{(a²+B²)} = \frac{Bx + C}{a² + b²}

6. For Repeated Irreducible Quadratics (Degree of 2 and k):

   1. \frac{…}{(a² + b²)^k} = \frac{B_1 x + C_1}{(a² + b²)^1} + \frac{B_2 x + C_2}{(a² + b²)²} + … + \frac{B_k x + C_k}{(a² + b²)^k}

x polar-to-Cartesian coordinate transformation

x=r\cos(\theta)

y polar-to-Cartesian coordinate transformation

y=r\sin(\theta)

Equation of a Circle in Cartesian coordinates

x² + y² = r²

Tangent Relation in Polar Coordinates Equation

\frac{y}{x} = \tan(\theta)

Area in Polar Coordinates Formula

\frac{1}{2} \int r² d\theta

Arc Length in Polar Coordinates Formula

\int \sqrt{r² + f’(\theta)²} d\theta

Divergence Series Test

• if \lim_{n \to \infty}{a_n \ne 0} , the serries diverges

• if \lim_{n \to \infty}{a_n} = 0, the serries is inconclusive (might converge/diverge)

Conditions of the Integral Test

• Continuous: (without breaks, jumps, or discontinuity)

• Positive: All values in the function must be positive

• Decreasing: As x increases, f(x) should get smaller/same and never increase

  • The integral test can be applied if f(x) is initially increasing. As long as it’s decreasing after some point N, the integral test works for n=N

What are the two kinds of comparison tests for series?

1. Direct Comparison Test

2. Limit Comparison Test

Direct Comparison Test

For a given sum \sum{a_n} choose a sum \sum{b_n} that is similar & \leq a_n in a more basic form. If \sum {b_n} converges/diverges, \sum{a_n} converges/diverges

• Ex: a_n = \frac{1}{n² + 1}, \text{choose } b_n = \frac{1}{n²} Because b_n \leq a_n and b_n converges (p-serries), a_n converges too

Limit Comparison Test

For a given sum \sum a_n choose a sum \sum b_n where if the limit exists/is infinity for \lim_{n \to \infty} \frac{a_n}{b_n} , the series converges/diverges

Ratio Test When to use & Formula

• Factorials (n! \text{ or } (2n)!)

• Exponential Expressions (a^n \text{ OR } \frac{3}{4}^n)

• L = \lim_{n \to \infty} |\frac{a_{n+1}}{a_n} | if L<1: Converge, L=1: Inconclusive, Else Diverge

Root Test When to use & Formula

• Functions with ONLY raised to nth power

• L = \lim_{n \to \infty} \sqrt[n]{|a_n|} If L<1: Converge, L=1: Inconclusive, Else: Diverge

Alternating Series Test General Form & Formula

• General Form: \sum_{n=1}^{\infty} (-1)^n \cdot a_n or \sum_{n=1}^{\infty} (-1)^{n+1} \cdot a_n

  • Where a_n is any function

• Condition 1: Terms must be decreasing

• Condition 2: \lim_{n \to \infty} a_n = 0

• If both conditions pass, the alternating series test converges conditionally

Telescoping Series General Form & Partial Sums

• General Form: \sum_{n = 1}^{\infty} (a_n - a_{n+1})

  • Where a_n - a_{n+1} will cancel out most of its terms

  • Where S is the total sum of the telescoping series

• Partial Sum: S_n = a_1 - a_{n+1}

  • a_1 - a_{n+1}

  • S = \lim_{n \to \infty} S_n

Taylor Series Formula Definition for f(x)

• f(x) = f(a) + f’(a)(x-a) + \frac{f’’(a)}{2!}(x-a)² + \frac{f’’’(a)}{3!}(x-a)³ + …

• General: f(x) = \sum_{n=0}^{\infty} \frac{f^{n}(a)}{n!}(x-a)^n

Taylor Series for e^x

\sum_{n=1}^{\infty} \frac{x^n}{n!}

Taylor series for sin(x)

\sin(x) = \sum_{n=0}^{\infty} (-1)^{n} \frac{x^{2n+1}}{(2n+1)!}

Taylor Series for cos(x)

\cos(x) = \sum_{n=0}^{\infty} (-1)^{n} \frac{x^{2n}}{(2n)!}

Taylor Serries Usually Converges using the _____ test

Ratio Test