Correlation & Regression

Pearson correlation

• appropriate for linear relationships

• two quantitative variables

• normally distributed data

Spearman correlation

• monotonic relationships

• quantitative/ordinal data

• based on the ranks of the data

standard deviation

• always positive

• normalises the covariance of variables (in Pearsons formula)

correlation

how much and in what direction one variable changes when the other variable changes

regression analysis

aims to create a predictive model

regression line

a mathematical equation that represents the relationship between X and Y

• to obtain the equation of the line that best predicts the value of the dependent variable Y based on the values of the independent variable X

main applications

• predicting treatment outcomes (prognosis)

• identifying risk factors (etiology)

regression line equation

Y=a+bX

a - the predicted value of Y when X is zero (intercept of the Y-axis)

b - the rate of change of Y for a unit increase in X (slope, steepness), direction and magnitude of relationship

least squares method

minimize the sum of the squared vertical distances (residuals) between the observed Y-values and the corresponding values predicted by the regression line

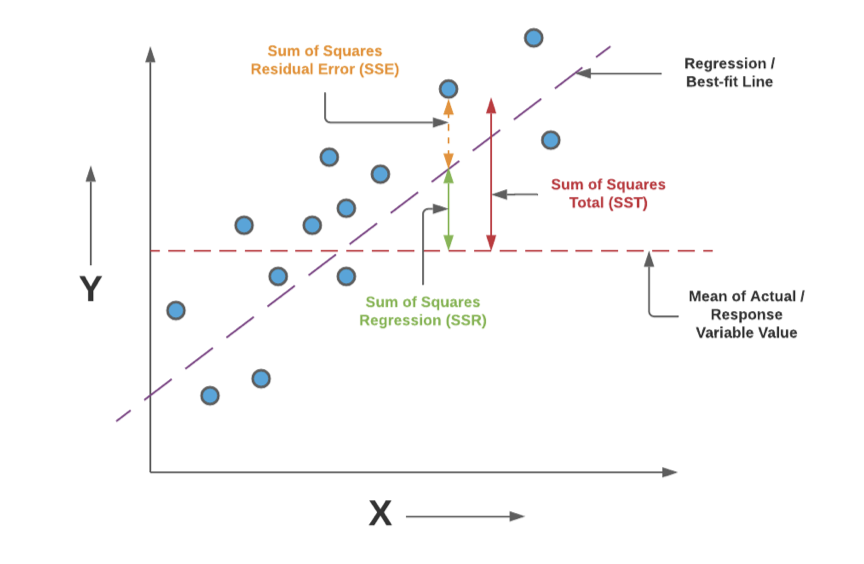
Sum of Squares Total

represents the total variability in the dependent variable (Y) without considering the effect of the independent variable (X)

Sum of Squares Residual Error

represents the unexplained variability in Y, or the variability that is attributed to random error or factors not included in the model

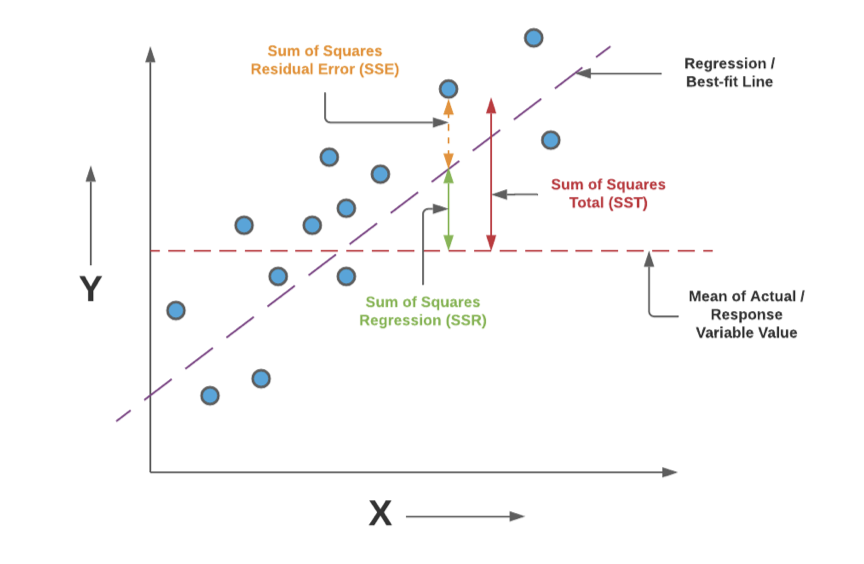
Sum of Squares Regression

measures the variability in Y that can be explained by the regression model, or in other words, the variability due to the independent variable (X)

R2 (the coefficient of determination)

the proportion of total variability explained by the model

• higher = better fit

• lower = more scattered points

R2=SSR/SST

* SST+SSRegression+SSError

F statistics

the overall significance of the regression model

taking the ratio of the Mean Square for Regression (MSR) to the Mean Square for Residuals (MSE)

• If the F-statistic is significantly different from 1, it suggests that the regression model is providing a better fit than a model with no independent variables.

Regression Degrees of Freedom

is equal to the number of independent variables in the regression model

Error Degrees of Freedom

Equal to the total number of observations minus the number of parameters estimated

the b coefficient

b is the estimated coefficient for the independent variable from the regression model

• is associated with a t-statistic,

• the null hypothesis is that the true population value of the coefficient is equal to zero

• H0: b = 0

t value

bx/SE(bx)

SE(bx)

square root of the residual Mean Squares divided by the Degree of Freedom associated with the residuals multiplied by the variance of the independent variable

Confidence interval for the b coefficient

coefficient for the independent variable from the regression model ± the critical value x the standard error of the coefficient