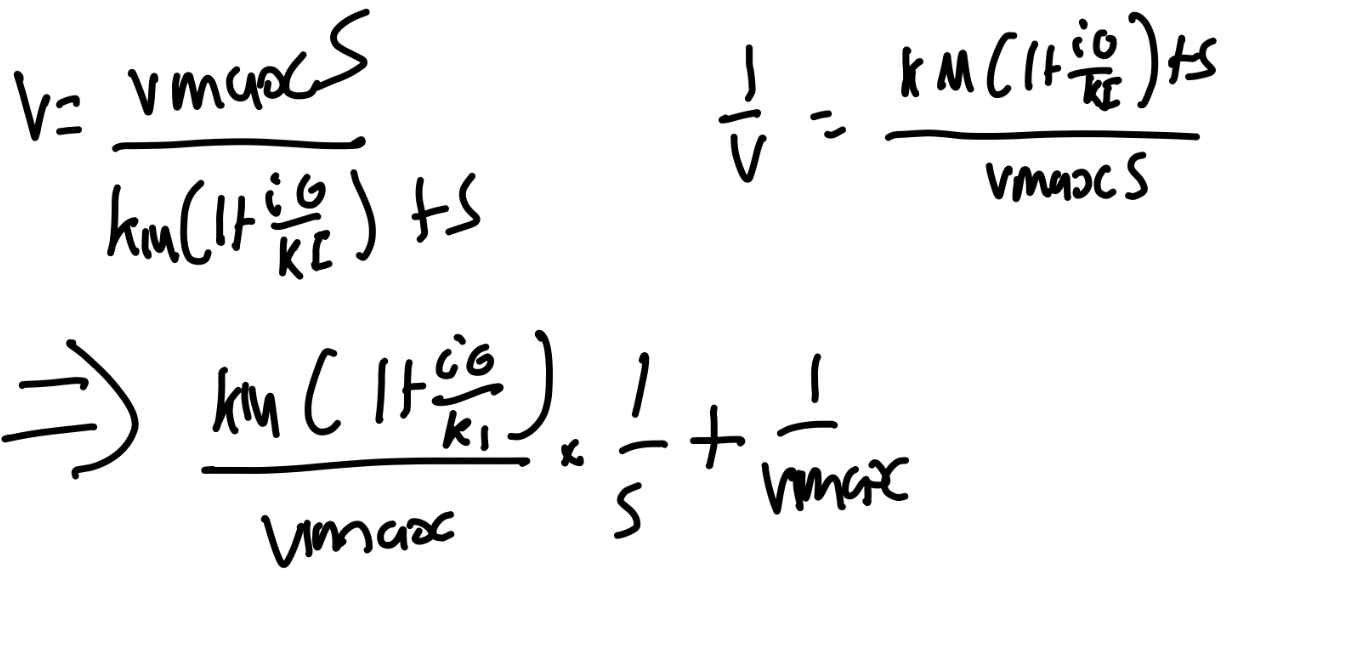Mechanistic Modelling

What is systems biology?

Study of biochemical systems within the body, enzyme reaction systems, gene regulation systems…

A cell consists of many different, unlinked ‘systems’. Different systems require different kinds of mathematical models appropriate for each system.

Describe reaction rates for unimolecular reactions (same as chem).

Describe reaction rates for bimolecular reactions.

What is the law of mass action?

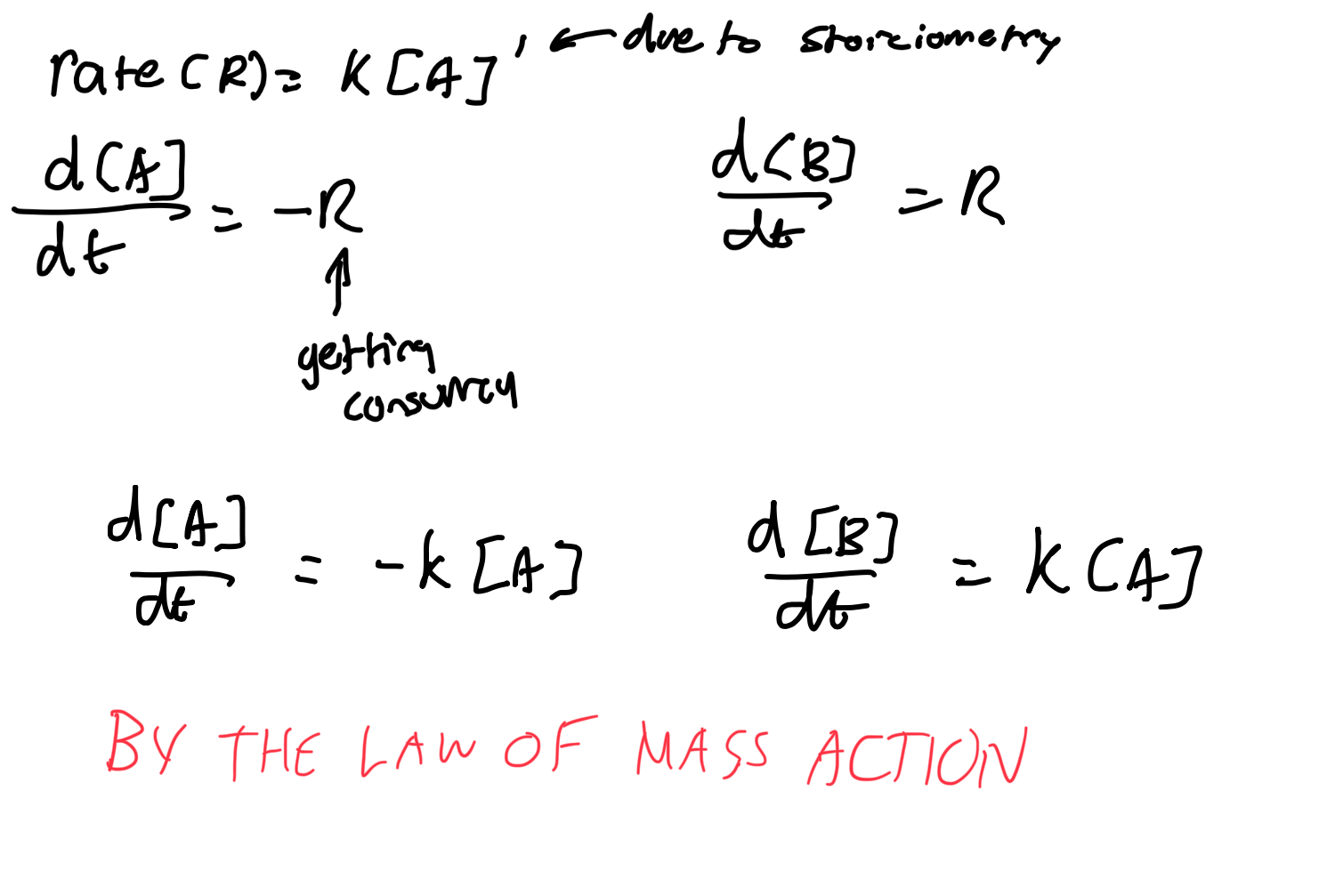
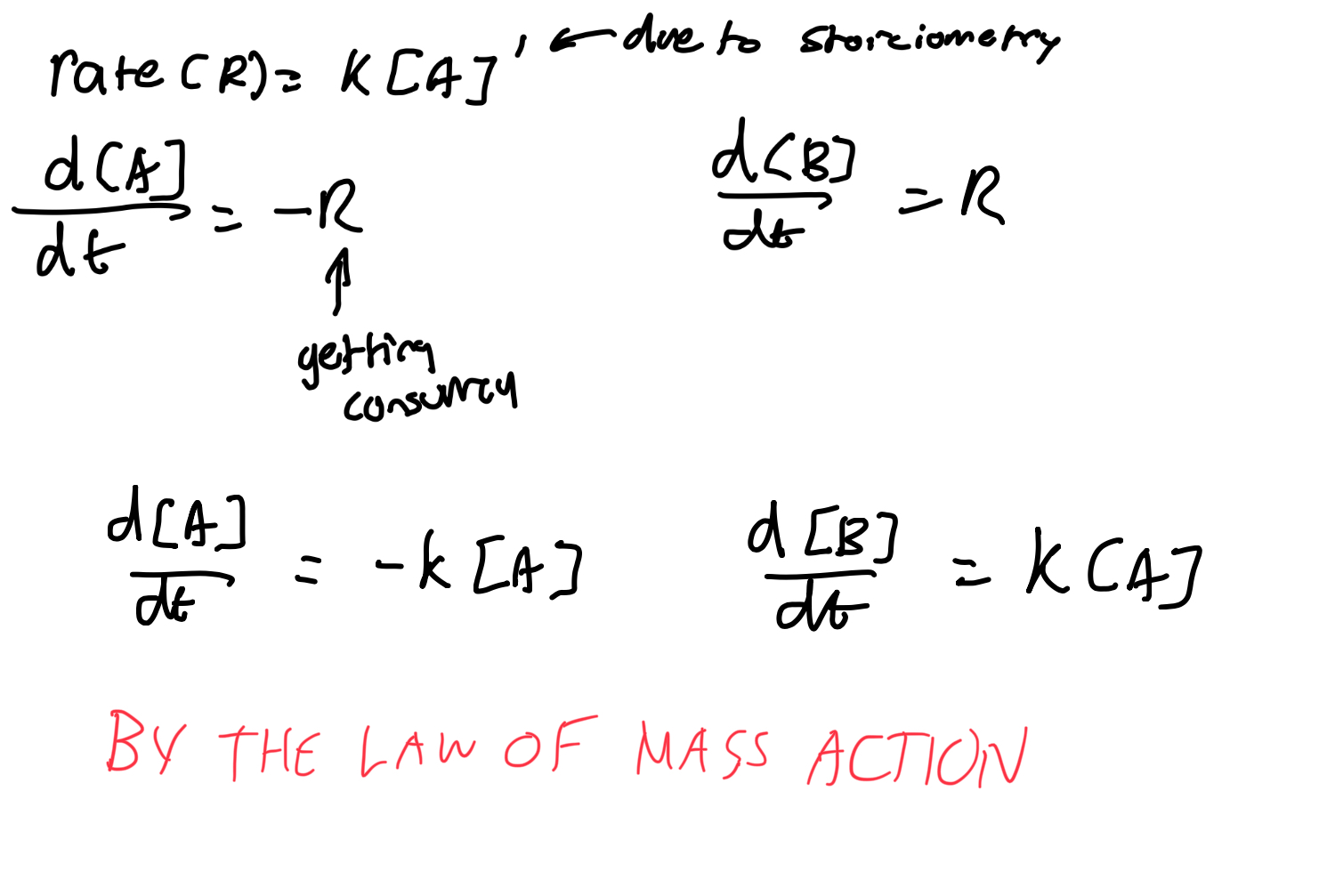
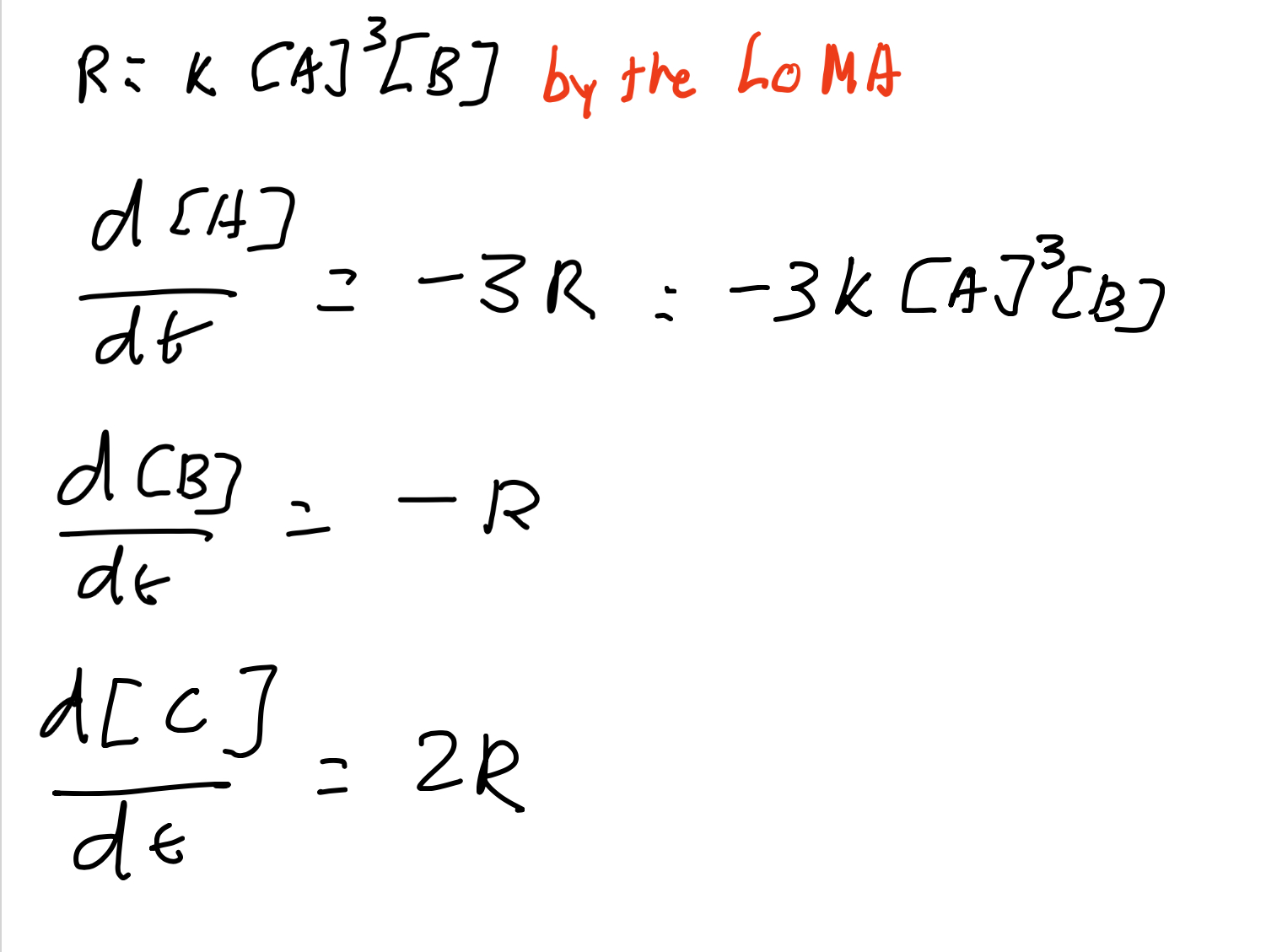
What are things to look for in a display of data?

Shape of the graph: symmetric, or skewed, unimodal or multimodal (number of peaks).

Location: where to find the centre of the distribution.

Spread.

Outliers.

Association between pairs of variables.

What is the general solution of a homogenous ODE dx/dt = ax?

x(t) = Ce^at, where C is an element in R is a constant.

The reaction A → B gave us the differential equation
d[A]/dt = -k[A]

Find the solution of the DE, if the initial concentration of A is [A]0 = 2M

Suppose that a reactant A is produced at a constant rate r M s^-1, while also decaying via the reaction A→B with mass action kinetics.
Write a DE for [A].

The rate of consumption of A due to the reaction A→ B is R=k[A]

so the DE for [A] is
d[A]/dt = rate of production - rate of consumption
= r - k[A]

This is an inhomogenous ODE

General solution: x(t)=y(t)+z(t)

What is the equation of an inhomogenous ODE?

dx/dt = ax+p(t)
These are solved using the Principle of Superposition.

Describe the principle of superposition.

Given dx/dt = ax+p(t)

X(t) = y(t) + z(t)

General sol is x(t) = y(t) + z(t)
Where
y(t) = Ce^at of the homogenous equation dy/dt=ay
z(t) is a particular solution of the inhomogenous equation dz/dt=az+p(t)

What is the process off solving inhomogenous eqation?

Find the general solution of dx.dt = 3x-2.

Find the general solution of dx/dt+2x=e^-2t.

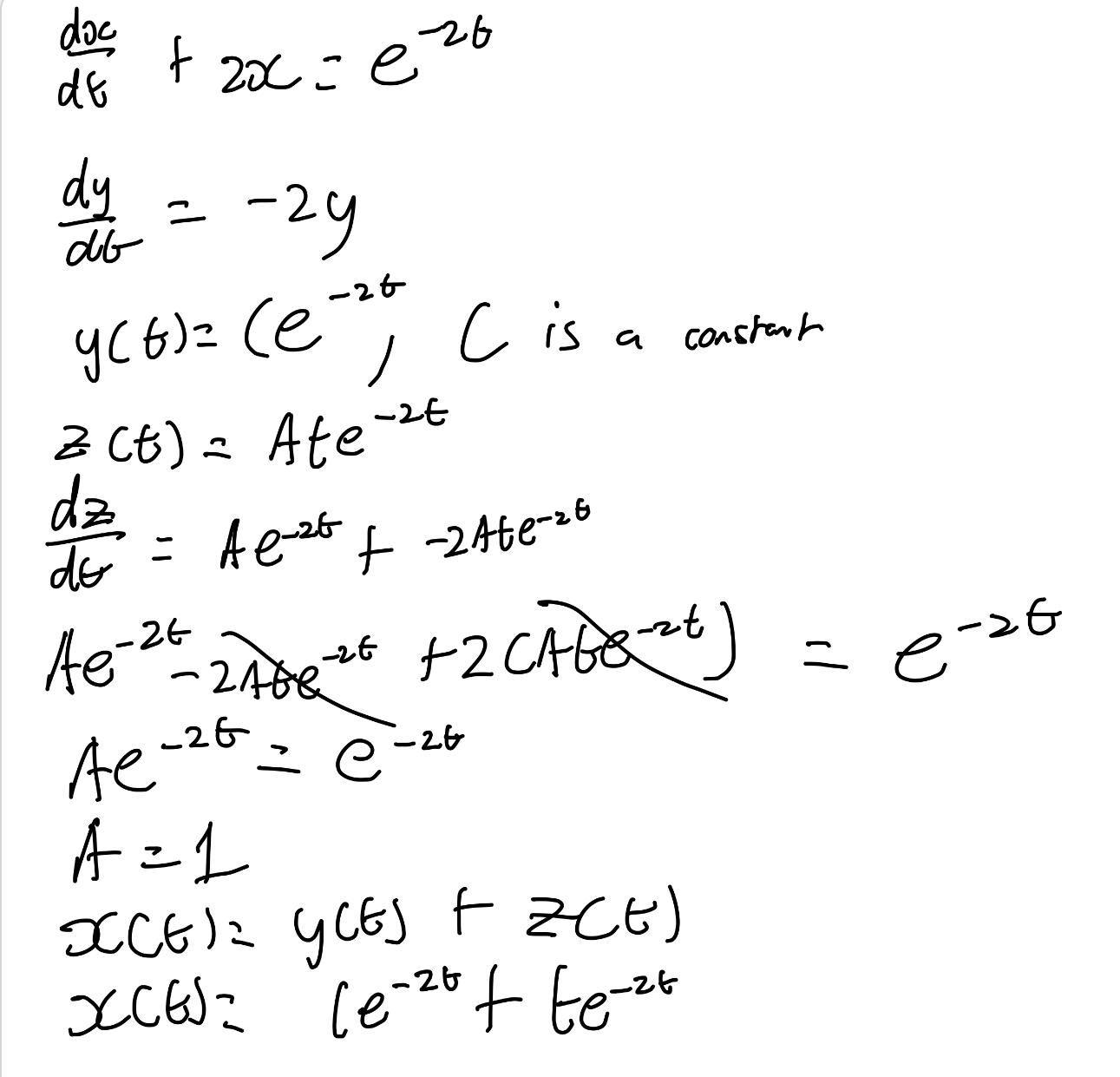
How to do equilibrium equation A←>B

https://imgur.com/a/G456gqh

repeat to yield [A]*

[B]*/[A]*=k1/k-1

Kc=k1/k-1

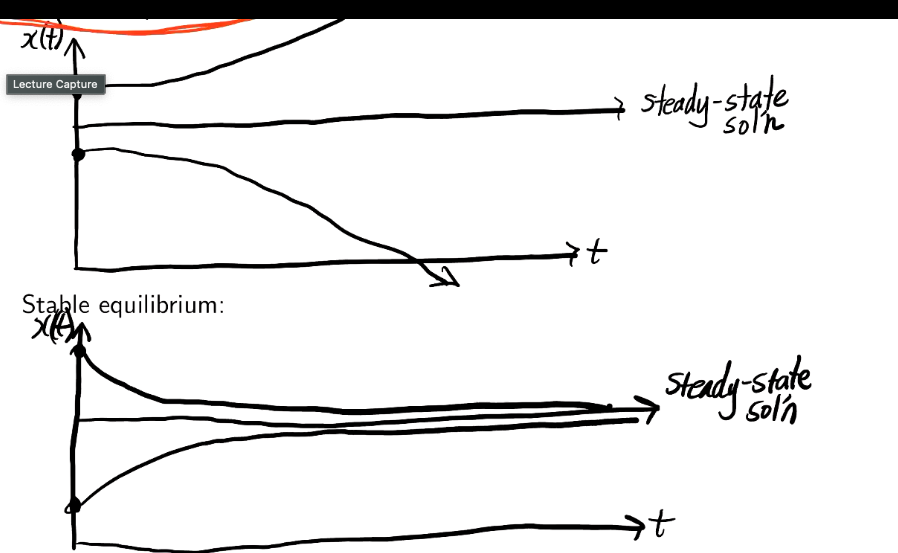
What is steady-state?

As t→infinity the concentration approaches constant values: the equilibrium or a steady-state solution.

What is stable or unstable equilibrium? Graph them.

Stable if solutions that start close to the equilibrium move towards the equilibrium.

Unstable if solutions that start close to the equilibrium move away from the equilibrium.

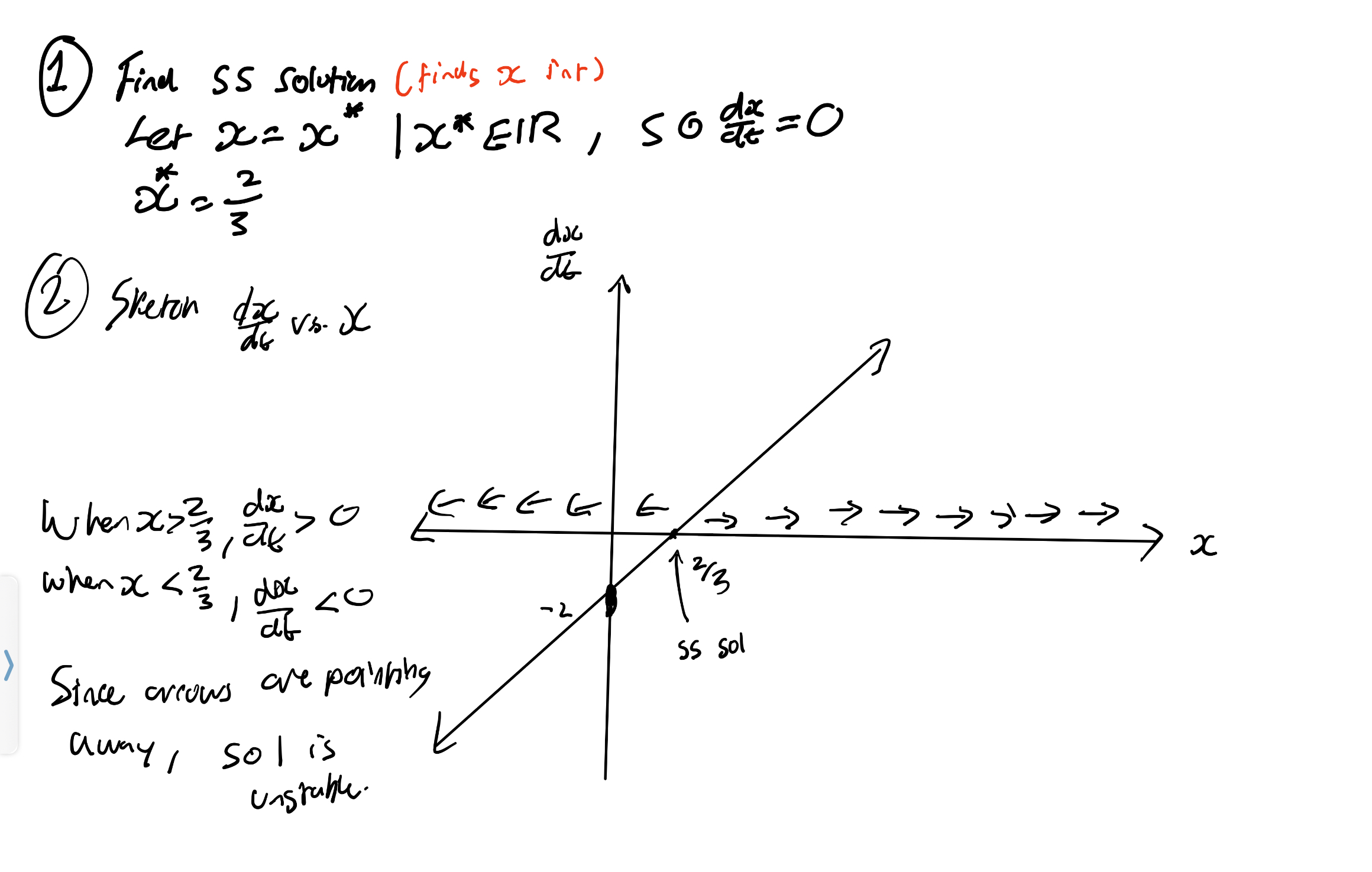
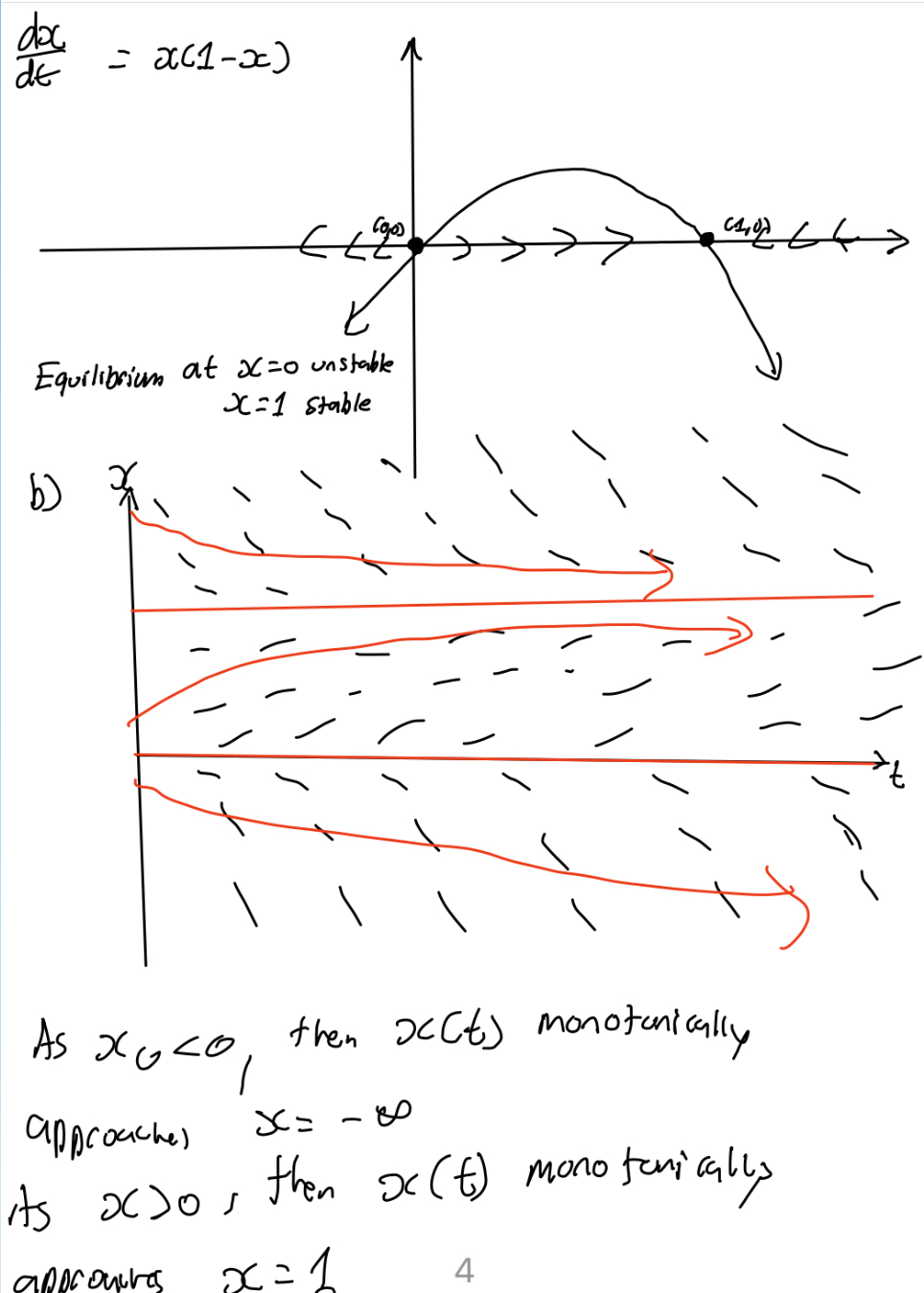
Find the equilibria of dx/dt = 3x - 2

If you were to sole such DE, x(t)=Ce^3t+2/3

Since e^3t → infinity as t → infinity, solution move away from x* = 2/3
→ x* = 2/3 is unstable.

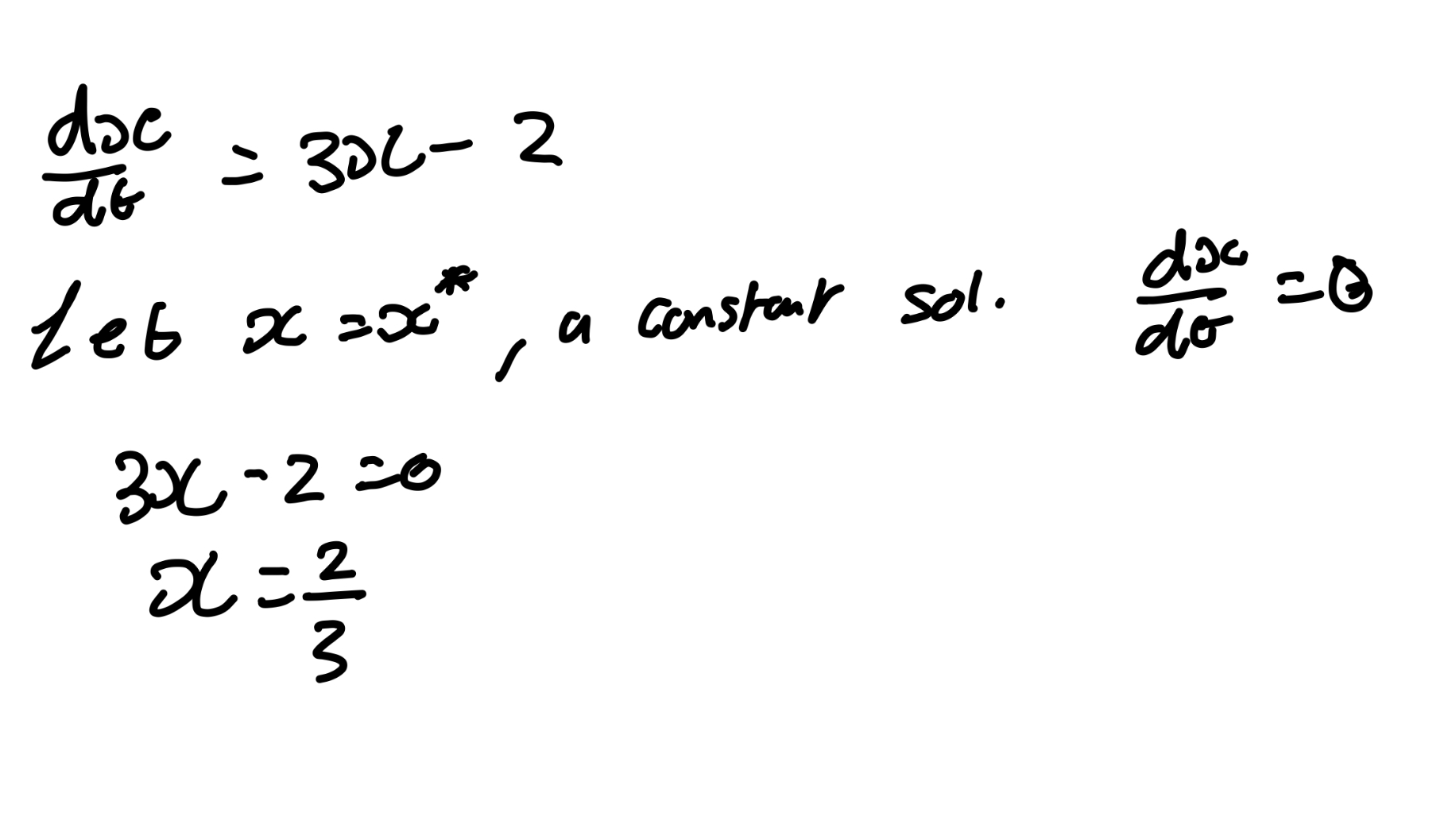
Draw phase line diagram for dx/dt = 3x-2

Phase diagrams only work when the RHS does not contain ‘t’ (autonomous).

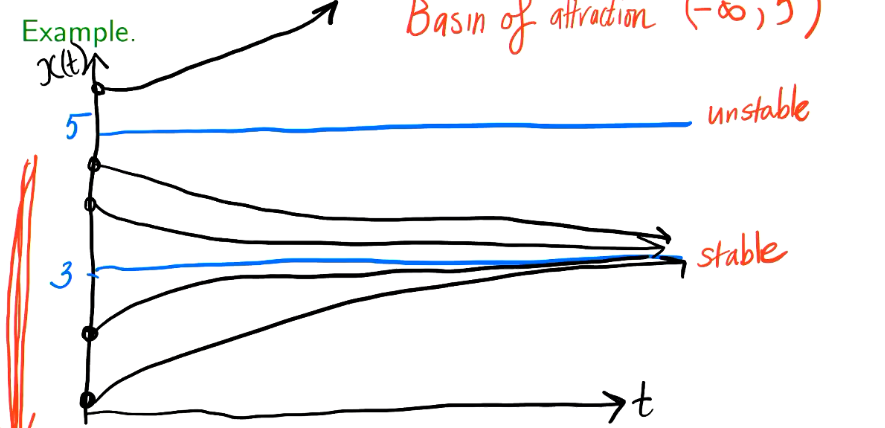
What is the basin of attraction?

The set of all the starting points — usually close to one another — that arrive at the same final state as the system evolves through time

Since the line above 5 does not subtend towards, 3, we don’t include it.

(- infinity, 5)

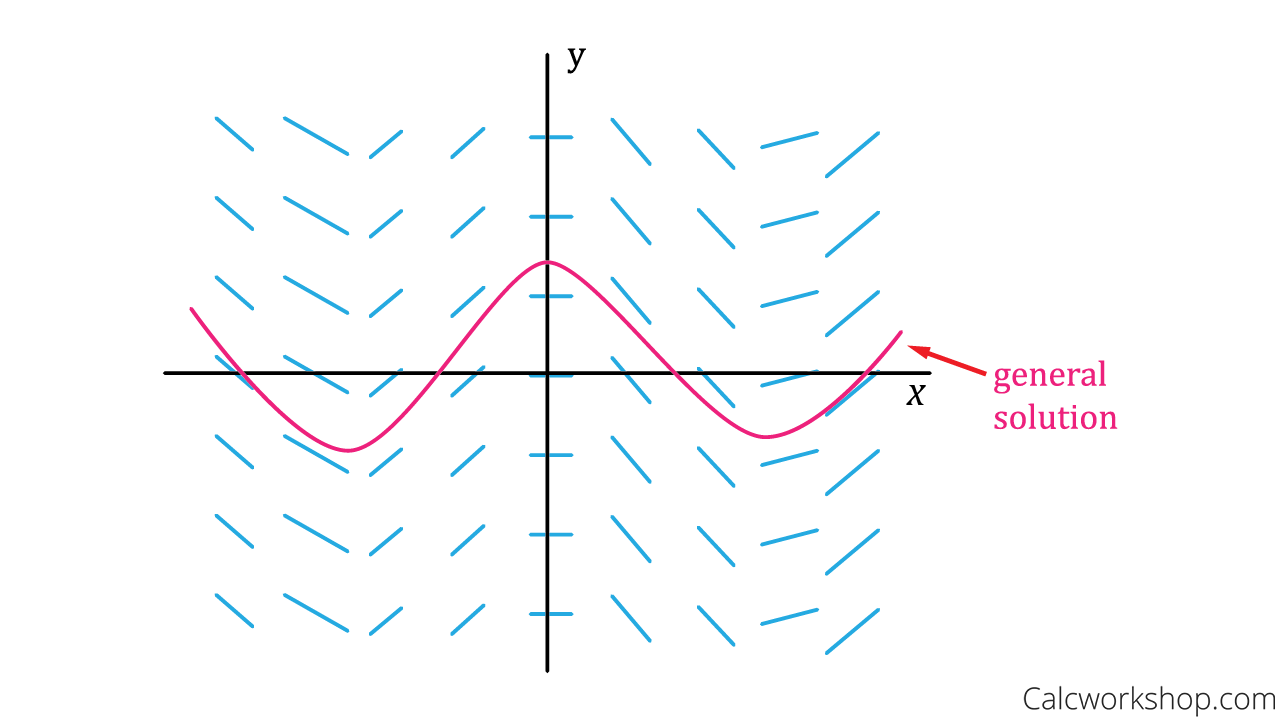
What is a direction field (slope field)?

General solutions of the DEs are curves that follow the arrows.

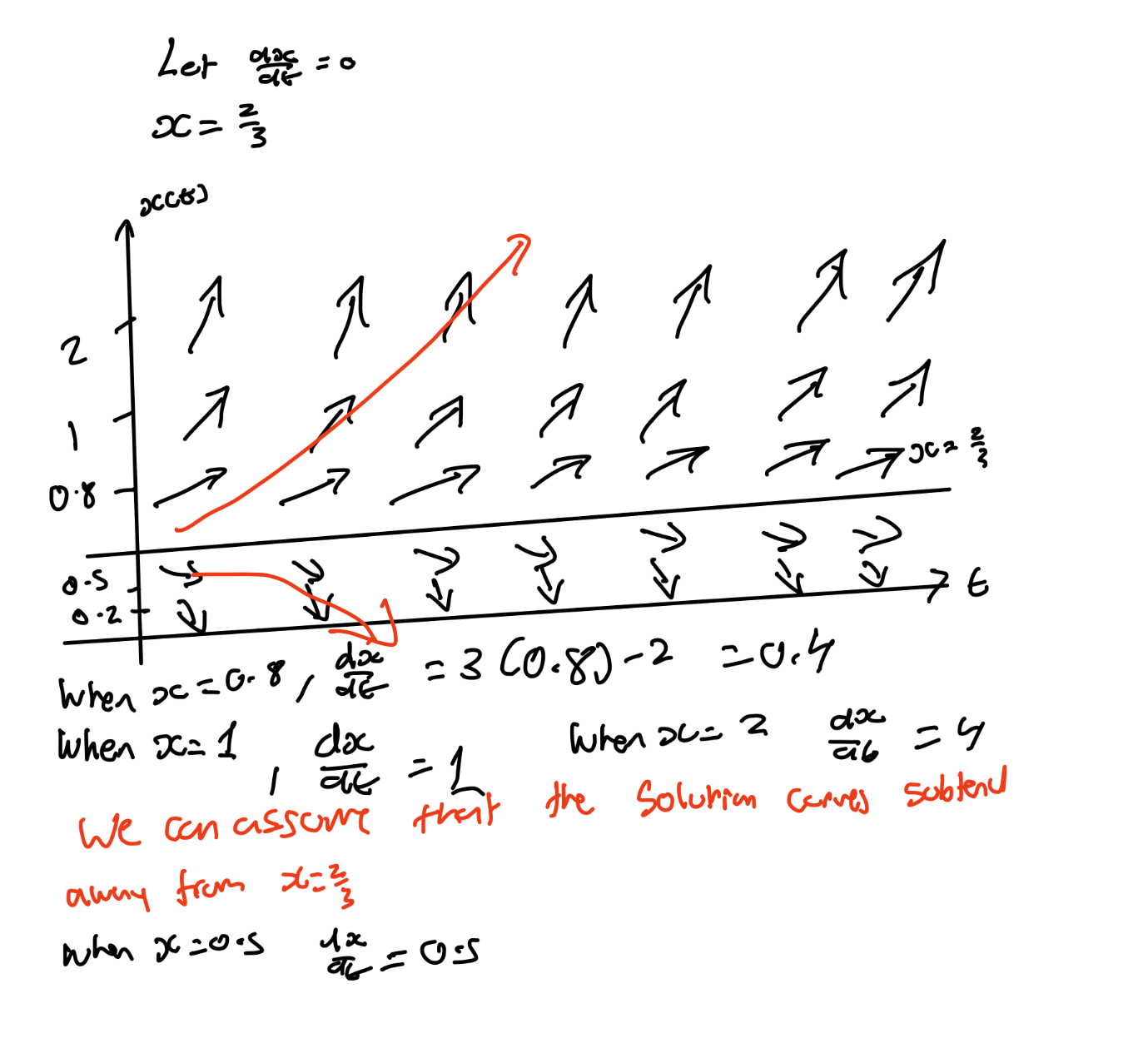
Draw the direction field for dx/dt=3x-2.

Consider the reversible dimerization reaction
2A←>(k1,k-1)B

Yield a phase line diagram and phase plane diagram (nullcline).

https://imgur.com/a/44LoUc6

Do qualitative analysis on the following reaction.

A-K1→B-K2→C

https://imgur.com/a/OsFH69Y

This tells us that a(t) decreases monotonically to 0.

b increases to a maximum, then decreases monotonically to 0.

If k1«k2, the horizontal nullcline, k1/k2a, gradient would be more flat. This means max of trajectory of b is lower (bc intermediate, b, is used instantly).

If k1»k2, the horizonal nullcline, k1/k2a, the gradient would be more steep. This means max trajectory of b is higher (bc intermediate, b, builds up.

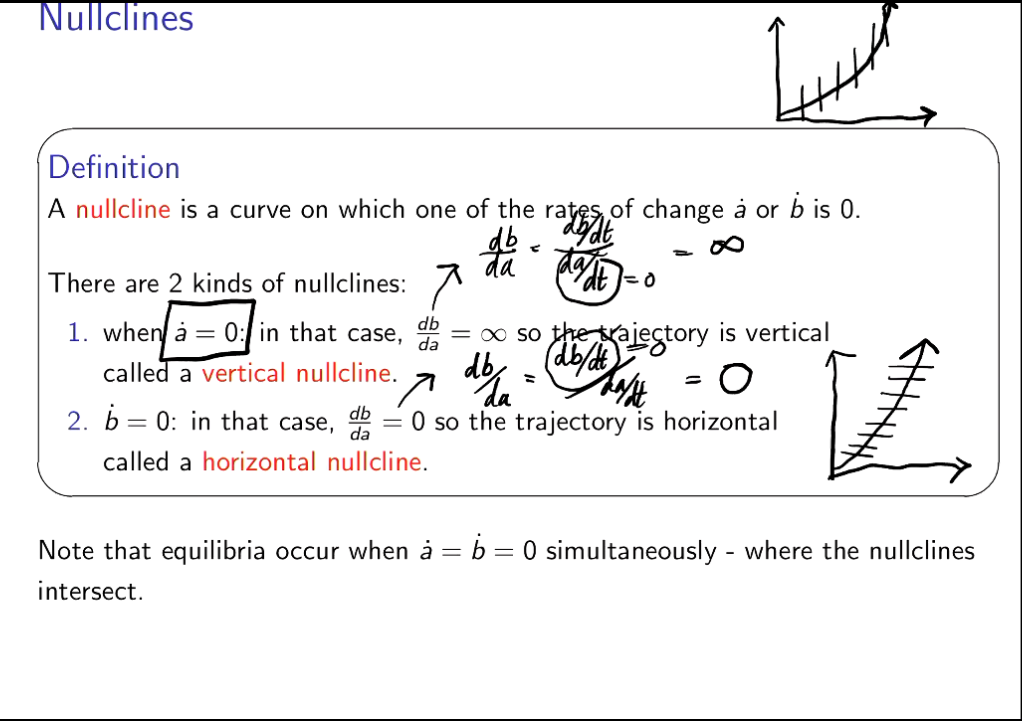
What is a nullcline?

as you are dividng by 0, thus it is infinity.

For a cell to operate, what must it do?

Get energy from the outside and use it to build chemicals/structures (metabolism).

Respond to signals from outside the cell (signalling).

Turn on/off processes, as needed (regulation).

All these operate via chemical reactions.

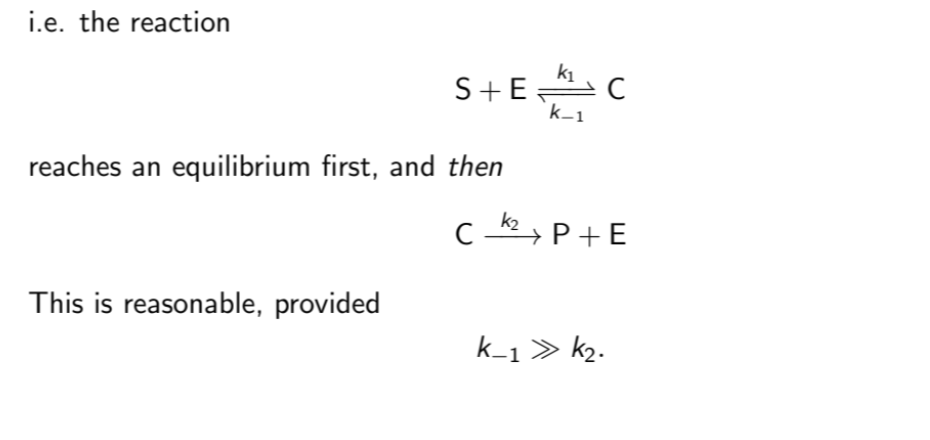
What is the Michaeis & Menten approximation?

They approximate the rate equation by assuming that the complex quickly reaches an equilibrium.

ds/dt is effectively 0

c is roughly e0s/(KD+s) where KD=k-1/k1

c is roughly e0s/(KM+), where KM=(k-1+k2)/k1

KD=KM

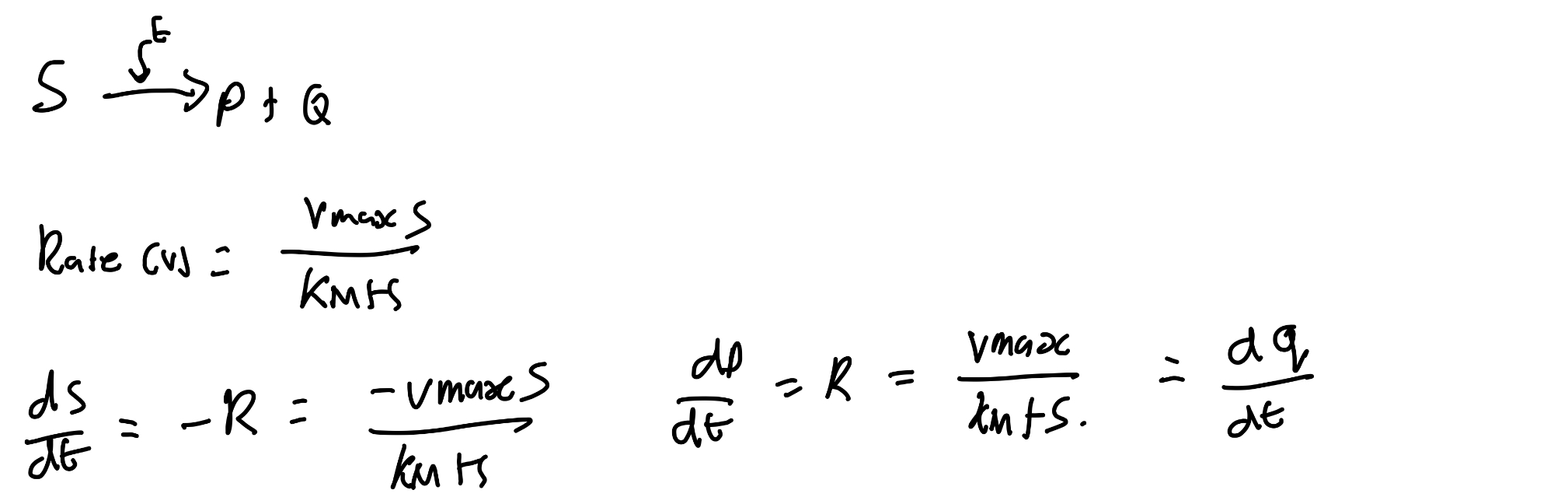
What is the issue with Michaelis-Mentis kinetics?

Rate of production shows a more rapid saturation.

Hill’s kinetics counters this.

What is Hill’s kinetics.

KH is the Hill constant.

h≥1
Id h=1, Hill kinetics reduces to MM kinetics.

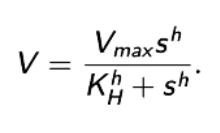
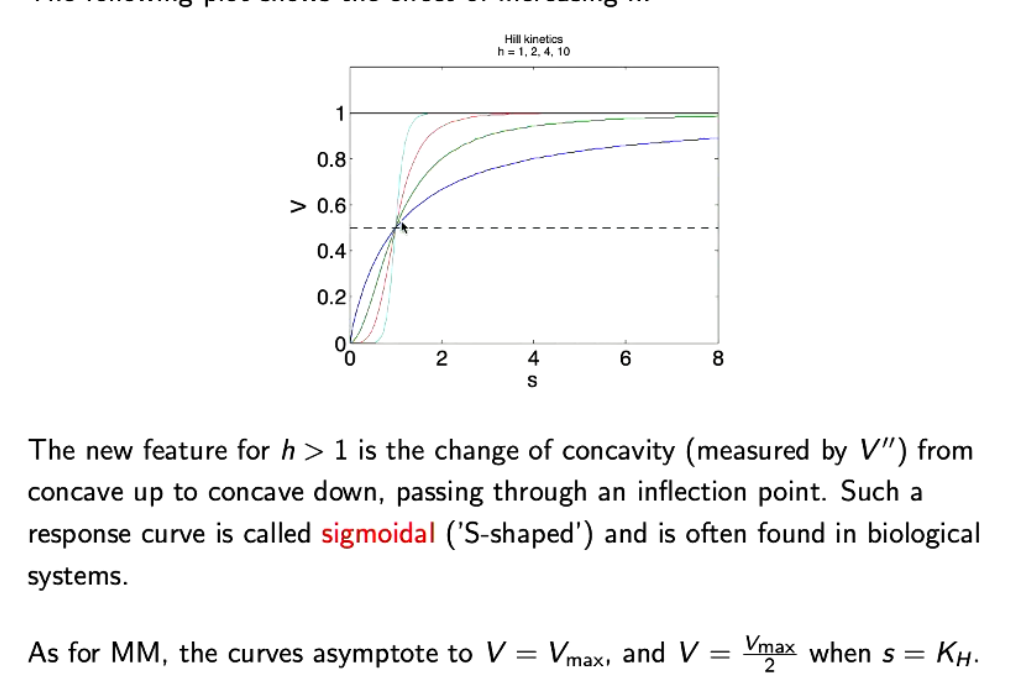
What happens when h increases in Hill’s kinetics.

Blue line is MM.

As s increases, concavity changes (concave up to concave down). Has a sigmoidal (s-shaped) curve.

Asymptote at V=Vmax, and V=Vmax/2 when s=KH

Also becomes more steeper and reaches Vmax faster. (conc of products increases faster, but hits vmax faster). A higher h is good for a faster response, but bad for a prolonged response.

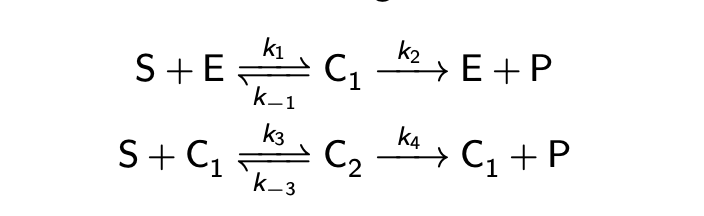
Derive rate law.

Given that rate law, what happens if k2 is small?

What is cooperative?

Here we have a situation where, having bound one substrate to the enzyme,

binding the second is easier/faster.

This is called (positive) cooperative binding and is seen in many proteins which

have several active sites.

A classic example of this is hemoglobin: binding of O2 to hemoglobin becomes

easier as more O2 is already bound.

Simple cooperative binding is Hill kinetics with h=2.

What are the equations for enzyme inhibition?

Derive the equations for inhibition and enzyme-substrate complexes.

https://imgur.com/a/UeRYx00

More inhibitors increases KM’
Since KM’>KM, the reaciton is slowed down (For a fixed value of s and e0), as expected.

However, Vmax is unchanged.

Under usually laboratory conditions, where e0«s0, i0, the complex concentrations stay small, so we can replace i with i0.

Use QSSA for SE, where KM is the Michaelis constant.

Use QSSA for EI, where K1=k-3/k2 is the dissociation constant for the EI.

Then, find overall reaciton velocity, V.

What is the Lineweaver-Burk plot?

y-int is 1/Vmax

slope = KM/Vmax

How to do Lineweaver-Burk plot with inhibition.

Since on a Lineweaver-Burk plot, the slope is given by KM/Vmax, if we see plots with the same intercept but slope increasing as the amount of inhibitor i0 is increased. Then this indicates inhibition as investigated earlier.