Math 210 Exam #1

Commutative Property of Additon

Changing the order of the addends does not change the sum.

a+b=b+a

Commutative Property of Multiplication

Changing the order of the factors does not change the product.

ab=ba

Associative Property of Addition

Changing the grouping of the addends does not change the sum.

(a+b)+c=a=(b+c)

Identity property of Addition

Adding zero to any number leaves that number unchanged.

a+0=0+a=a

Identity Property of Multiplication

Multiplying any number by 1 leaves that number unchanged.

a x 1= 1 x a=a

Zero Property of Multiplication

Multiplying any number by 0 gives 0.

a x 0=0 x a= 0

Distributive Property of Multiplication over Addition

a(b+c)=ab+ac

Distributive Property of Multiplication over Subtraction

a(b-c)=ab-ac

Look for a pattern

The problems information, predicted work, or possible answers feature some repetition.

Make a table or list

There are several options/ lots of information to keep organized.

Examine a simpler problem

The problem numbers are too big or the situation too complicated.

Write an equation/ use algebra

The answer is an unknown number AND the problem gives enough info to create a relationship.

Write an equation/ use algebra

There is a commonly know formula.

Draw a diagram or picture

The problem contains info that you want/ need to visualize.

Guess and Check

There are a reasonable number of possible option’s.

Guess and Check

The problem give a value or condition to check them against.

Work backwards

Gives clear story or chain of events.

Work backwards

Know the end and need to find out about the beginning.

Use elimination

The problem involves a possibility that can be ruled out.

Use direct arithmetic/ reasoning

Requires straight forward operation.

Use direct arithmetic/ reasoning

Numbers with no additional interpretation.

Break into cases

Problem features totally separate qualities or situations.

Polya’s Four steps

Used for problem solving

Polya’s Four steps

Understand the problem, Devise a plan, Carry it out, Look back

Understand the problem

Vocabulary and Terms

Devise a plan

Something you will try and Looking at characteristics to devise a plan

Carry it out

Writing/ working happens here and Addresses improvements

Look back

Is the answer reasonable and Did we answer + was it what was asked

Repeating Sequence

Repeats the same block of items over and over

Repeating Sequence

123,+,123,+….

Difference Sequence

Describes how the main sequence behaves

Difference Sequence

1,3,5,15,17,51,…

Fibonacci Sequence

Always adds two terms to create the next term

Fibonacci Sequence

1,1,2,3,5,8,13,21,…

Arithmetic Sequence

Always adds the same amount to one term to make the next term

Arithmetic Sequence

13,28,43,58,…

Geometric Sequence

Always multiply by the same amount to turn one term into the next

Geometric Sequence

10,30,90,270,…

How

Describes steps and process

Why

Gives reason

Number sentence

Only uses numbers

Number sentence

2 × 3 + 1= 7

Equation

Has variables to be solved for

Equation

2x + 3 = 9

Expression

Has numbers and variable’s, but no equal sign

Expression

2x + 3

Addends

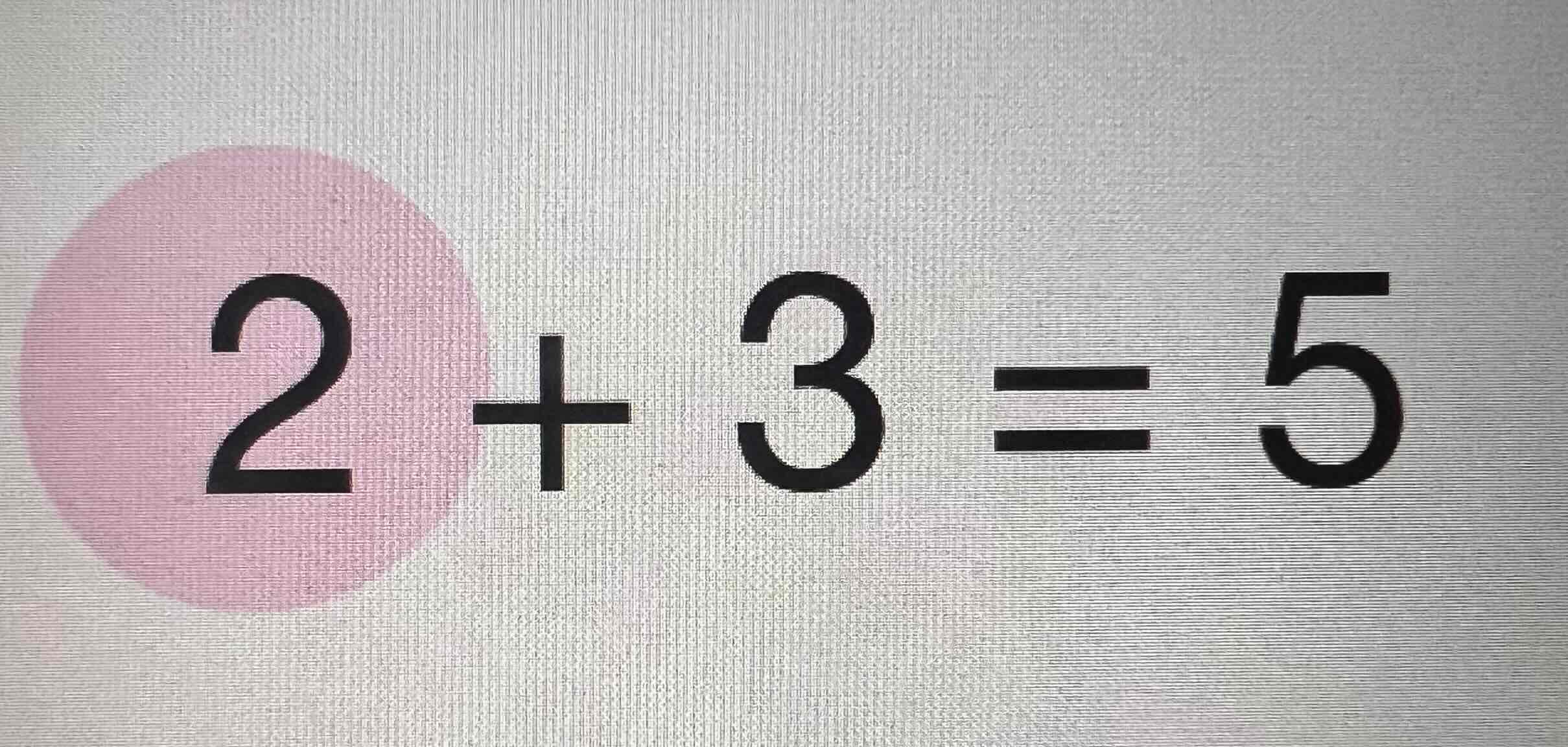
Sum

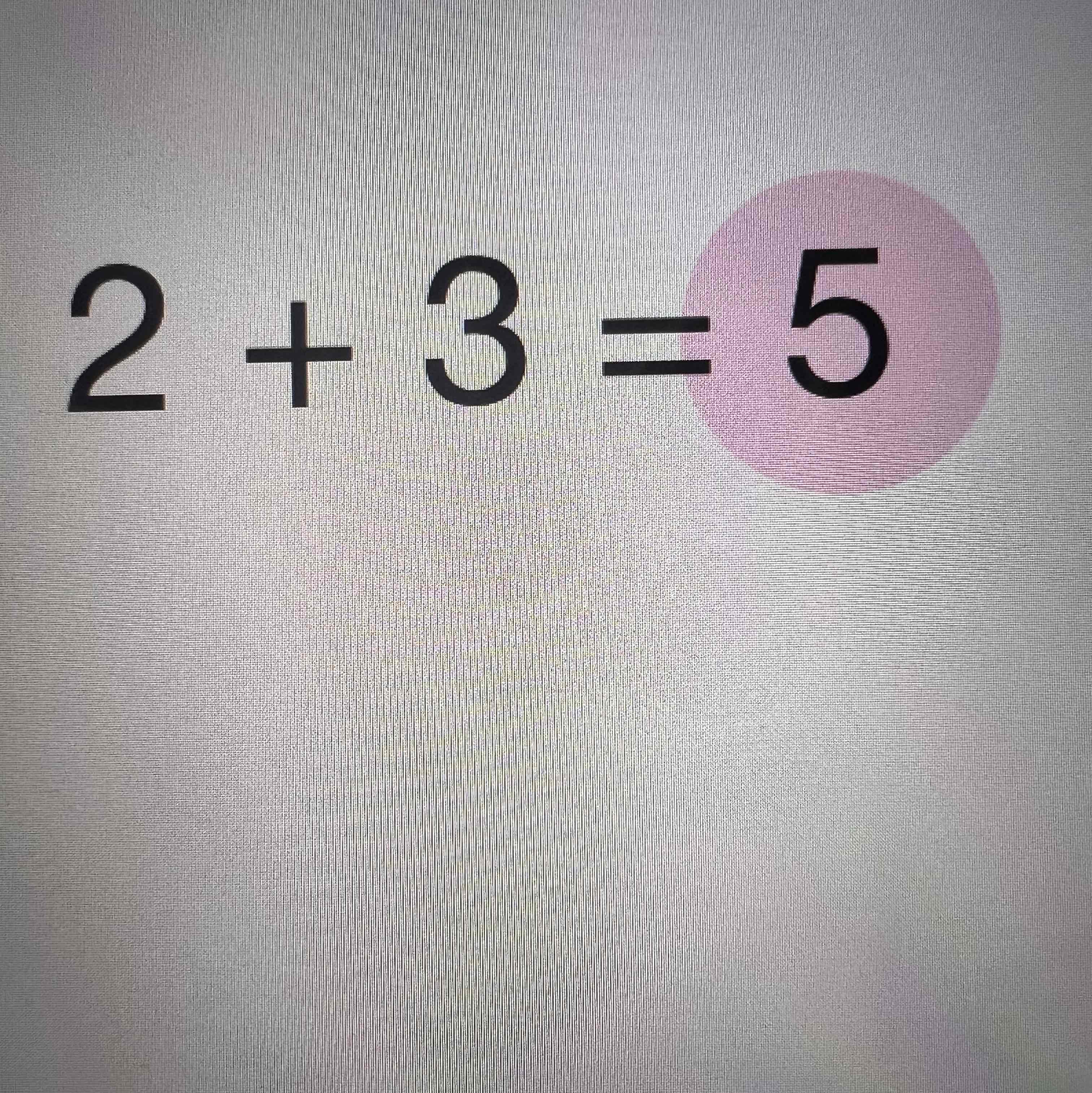
Minuend

Subtrahend

Difference

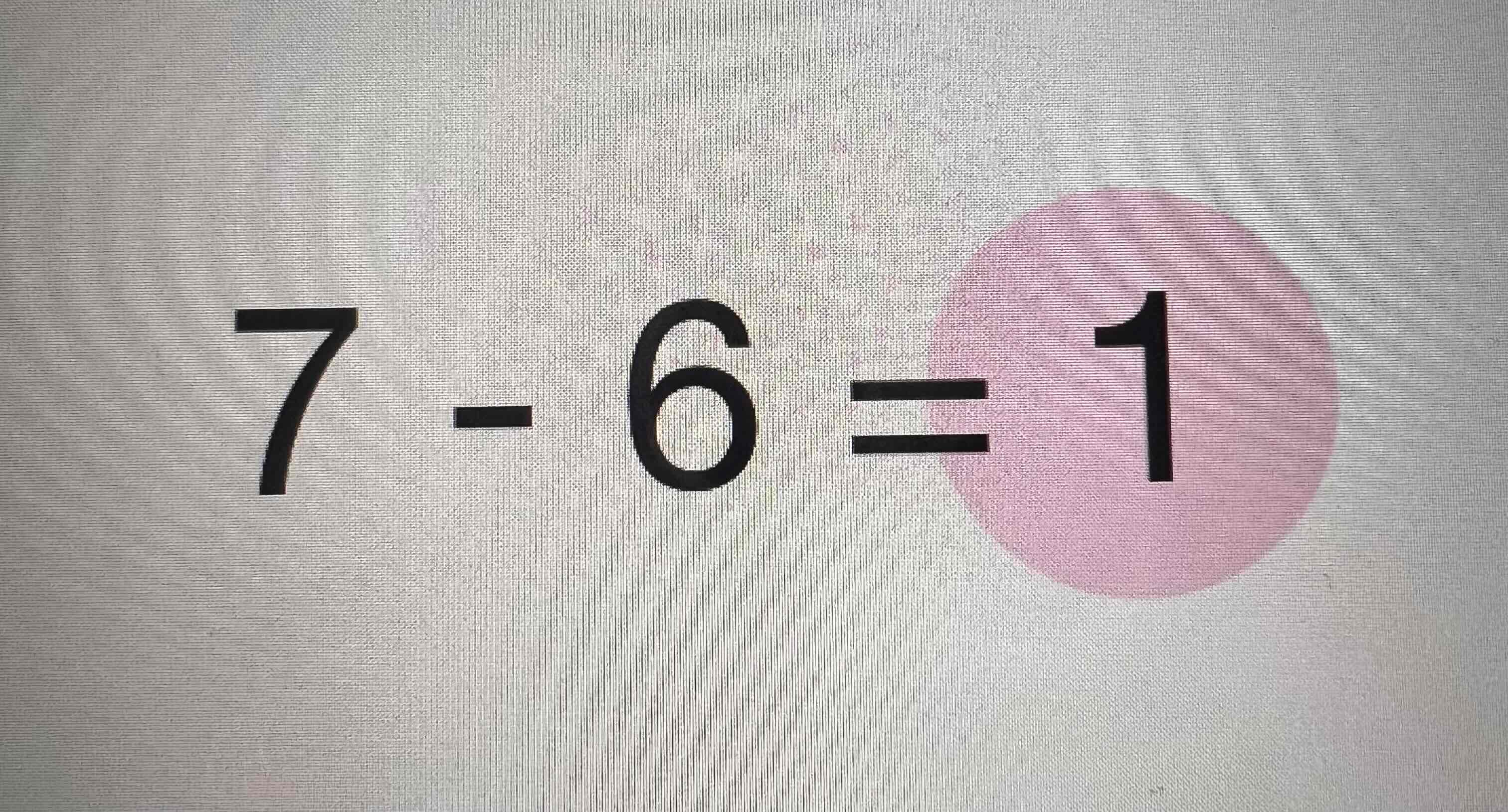
Factors

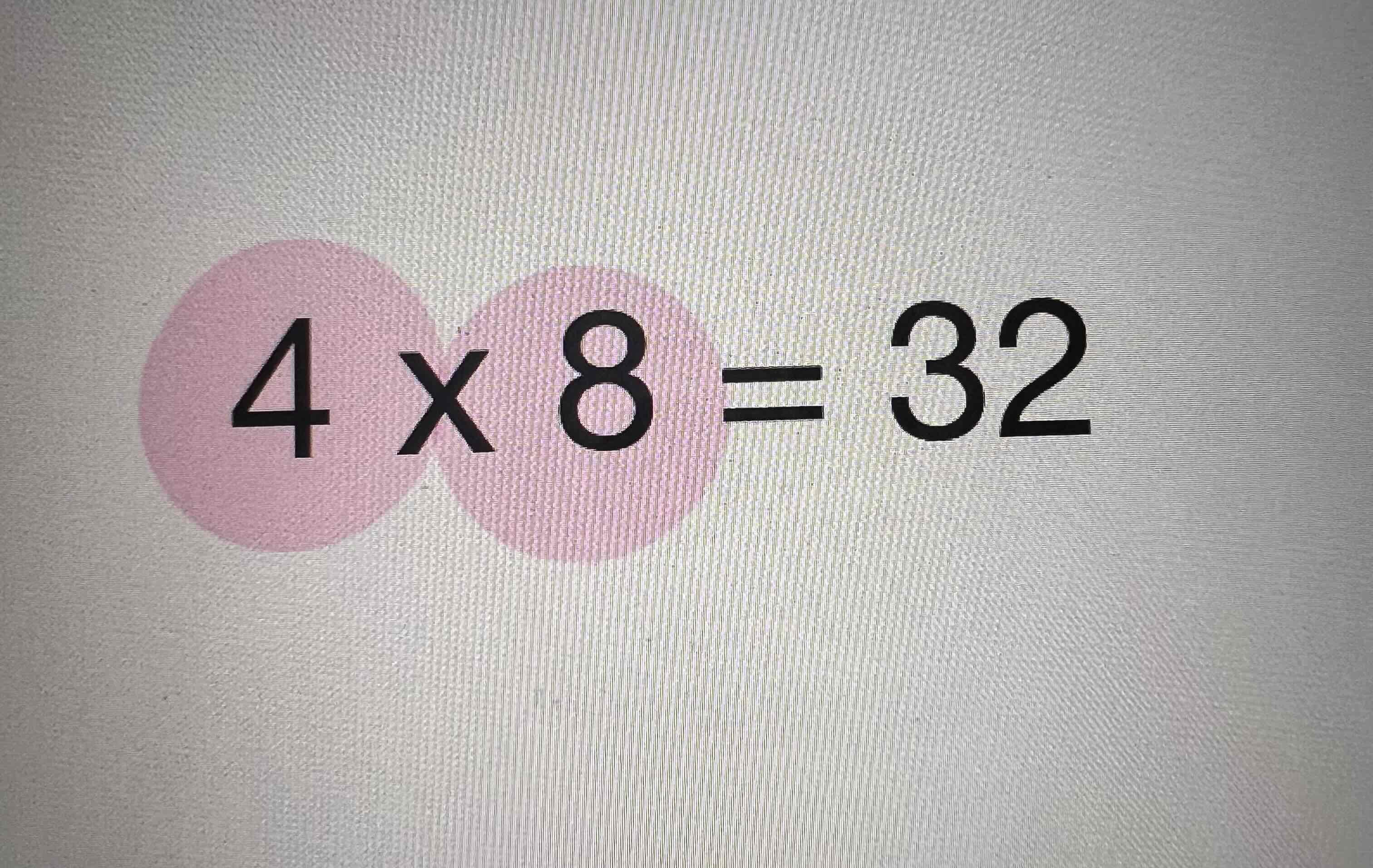
Product

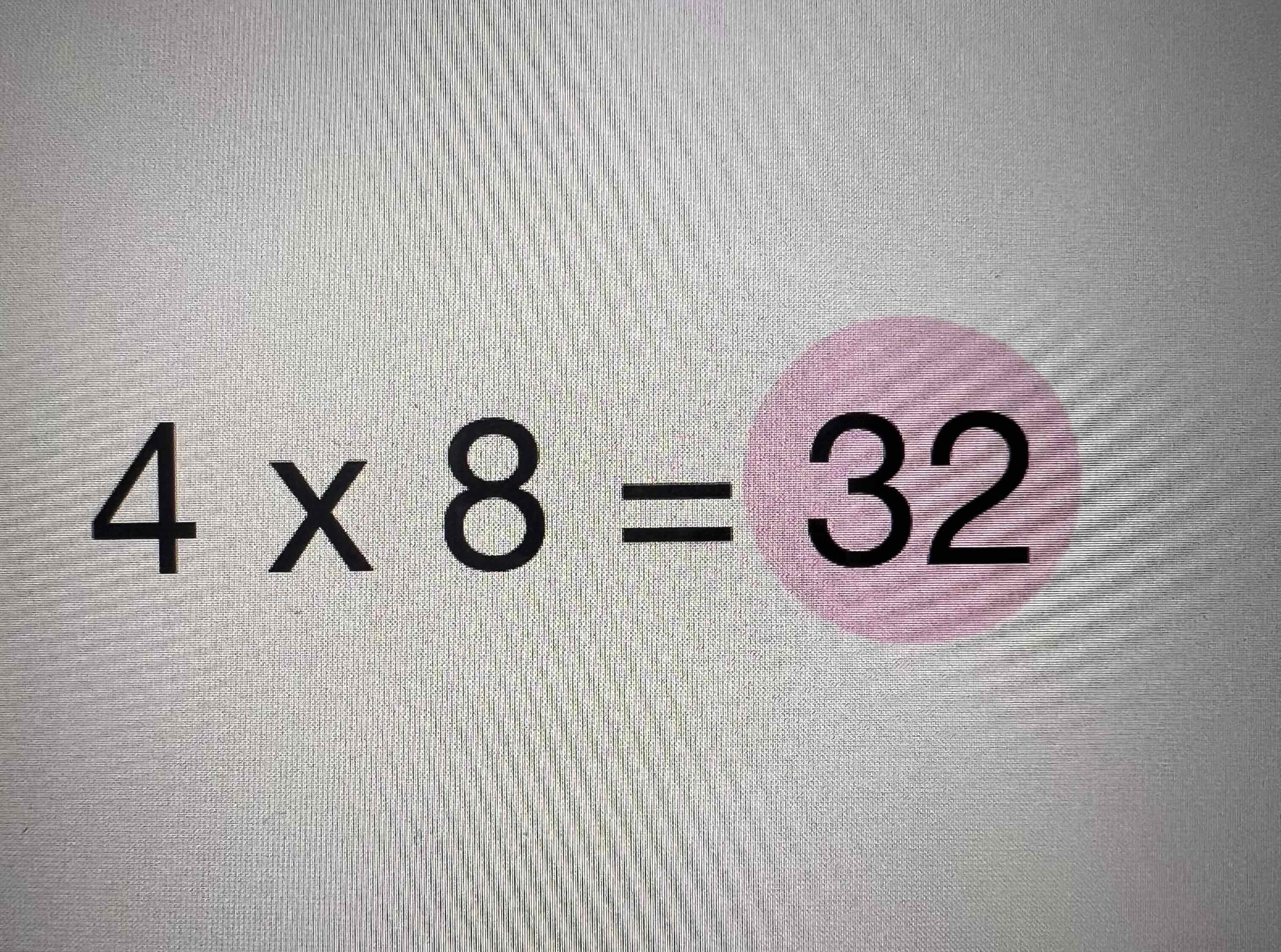
Dividend

Divisor

Quotient

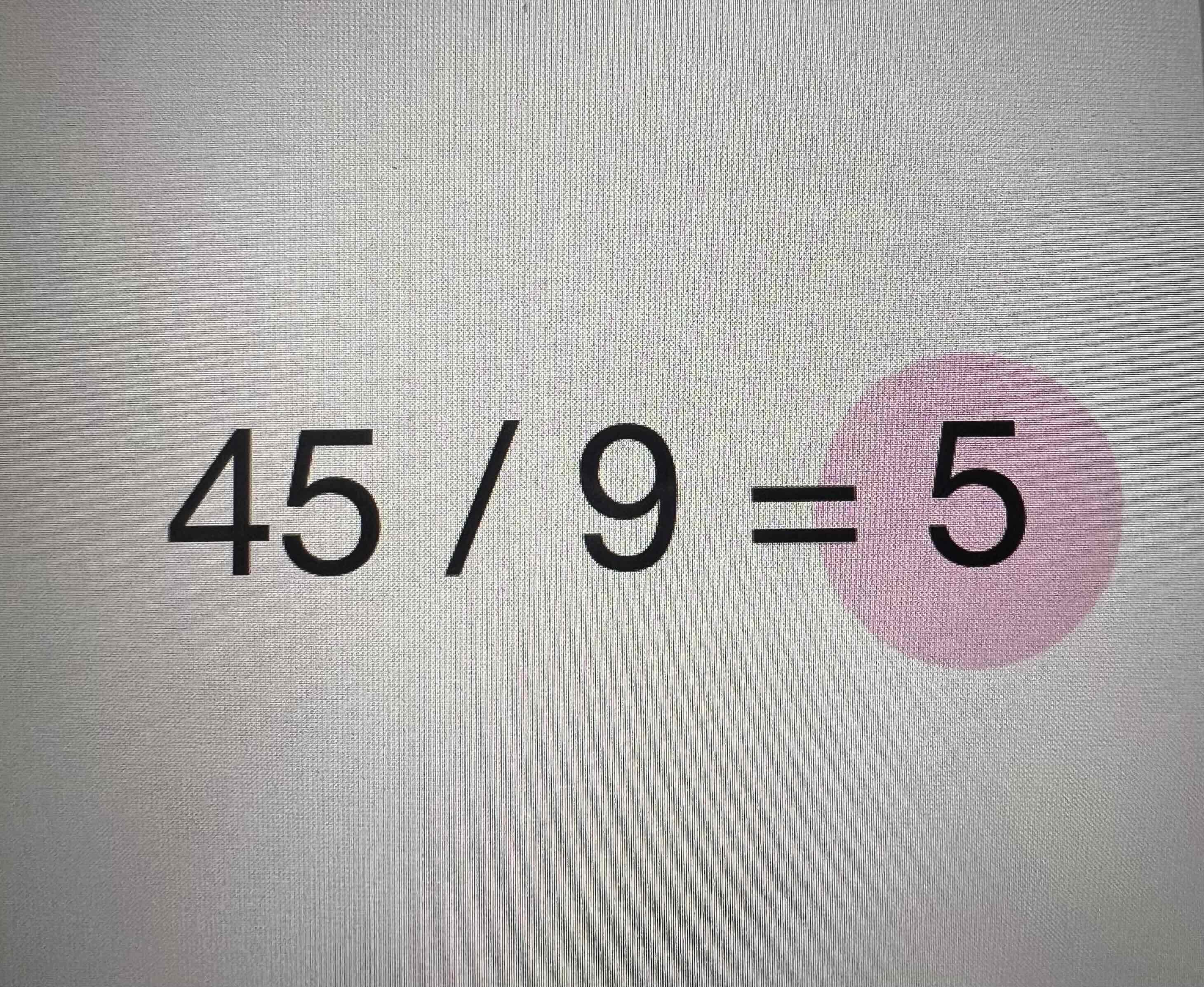
Identify a sub-goal

Steps that need to be done before anything else