Summer Homework

Unit circle, graphs, etc.

csc x

1/sin x

sec x

1/cos x

cot x

1/tan x

tan x

sin x/cos x

cot x

cos x/sin x

sin² x + cos² x

1

tan² x +1

sec² x

1+ cot² x

csc² x

slope intercept form

y=mx+b

Point slope form

y-y₁=m(x-x₁)

standard form

Ax+By+C=0

equation of circle

(x-h)²+(y-k)²=r²

a²-b²

(a-b)(a+b)

a³-b³

(a-b)(a²+ab+b²)

a³+b³

(a+b)(a²-ab+b²)

a⁴-b⁴

(a²-b²)(a²+b²)

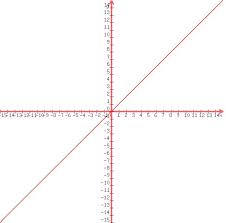
y=x

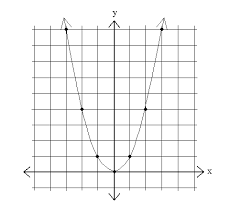
y=x²

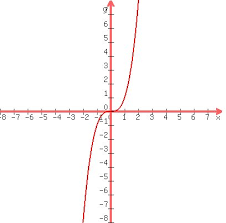
y=x³

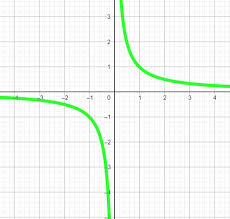
y=1/x

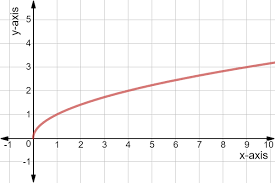
y=√x

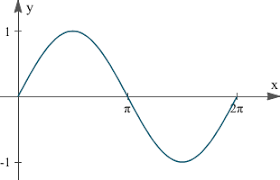
y=sin x

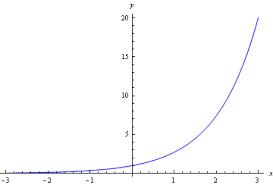
y=e^x

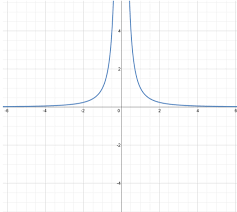
y=1/x²

y=3√x

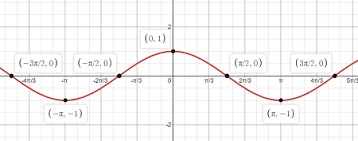
y=cos x

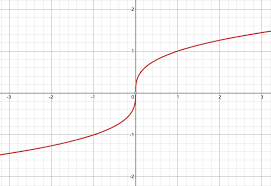
y=ln x

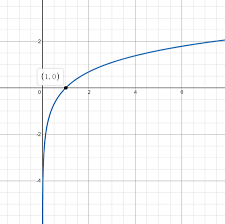
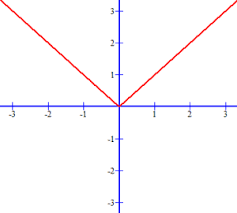
y=|x|

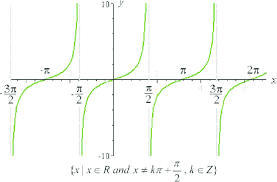
y=tan x

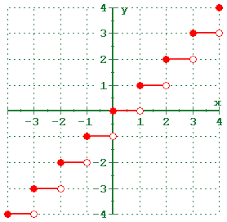
y=[[x]]

increments

the particle moves from point (x1, y1) to the point (x2, y2) where the coordinates are Ax=x2-x1 and Ay=y2-y1)

perpendicular slope

each slope is the negative reciprocal of the other

m1=-1/m2

m2=-1/m1

function

from a set d to a set r is a rule that assigns a unique element in r to each element in d

natural domain

when you define a function with a formula where the domain is not explicitly stated or restricted, the largest x and y values are assured to be the domain

a^x * a^y

a^x+y

a^x/a

(a^x)^y

(a^y)^x=a^x*y

a^x * b^x

(ab)^x

(a/b)^x

a^x/b^x

half-life

the amount of time it takes for half of the substance to change from its radioactive state to a non radioactive stae by emitting energy

compounded continuously

y=p*e^rt

base a logarithm function

y=logaX is the inverse of the base a exponetial function y=a^x

radian measure

of the angle acb at the center of the unit circle equals the length of the arc acb cuts from the unit circle.

sinx=y/r tanx=y/x secx=r/x

cosx=x/r cscx=r/y cotx=x/y

periodic

a function is this if there is a positive number p such as f(x+p)=f(x) for every value of x.

period

the smallest value of p is the ______ of x. Cosx, sinx, secx, and cscx are periodic with 2 pi and tanx and cotx are periodic with pi.

odd vs. even

cos x and secx are even the rest are odd functions

transformations

y=af(b(x+c))+d

where a=vertical stretch/shrink and a reflection about the x

b=horizontal stretch/shrink and a reflection about the y

c=horizontal shift

d=vertical shift

sine/sinusoid function

f(x)=A sin [(2pi/b (x-c)]+d

where a=amplitude

b=period

c=horizontal shift

d=vertical shift

average speed

found by dividing the distance covered by the elapsed time

limit

the function f has this as x approaches c if, given any positive number, there is a positive number for all x

polynomial and rational functions

if f(x)=a_nXⁿ + a_n-1X^n-1 +…+a^₀

^{if F(x) and g(x) are polynomials and c is any real number, then}

^{limx→ c f(x)/g(x)} =f©/g©, provided that g© does not equal zero

ex.lim x→ 3 [x²(2-x)]=(3²) (2-3)=-9

sandwhich therom

if g(x)<_f(x)<_h(x) for all x does not equal c in some interval about c and

lim x→c g(x)=lim(h(x)=L then limx→c=L

lim x→0 sinx/x

1

horizontal asymptote

the line y=b is this of the graph of the function y=f(x) if either limx→infinity f(x)=b or limx→-infinity f(x)=b

Sum rule

limx→+-infinity (f(x)+g(x)=L+M

difference rule

limx→+-infinity (f(x)-g(x))=L-M

product rule

limx→+-infinity (f(x)*g(x))=L*M

constant multiple rule

limx→+-infinity(k*f(x))=k*L

quotient rule

limx->+-infinity f(x)/g(x)=L/M when m does not equal zero

power rule

if r and s are integers, s does not equal 0, then limx→+-infinity (f(x)^r/s =c^r/s provided that L^r/s is a real number

removable discontinuity

each function has a limit of x→ o and we can remove the discontinuity by setting f(0) equal to its limit

jump discontinuity

the one sided limit exists bave different values 	

infinate discontinuity

fully seperated where limits are to infinity

osciliating discontinuity

it oscillates and has no limit at x→0

continuous on an interval

if and only if it is continuous at every point on the interval

continuous function

is one that is continuous on every point of its domain

properties of continuous functions

if the functions f and g are continuous at x=c, then the following combination are continuous at x=c.

composite of continuous functions

if f is continuous and g is continuous at f© then the composite gof is continuous at c

intermediate value theorm for continuouus functions

a function y=f(x) that is continuous on a closed interval [a,b] takes on every value between f(a) and f(b)In other words if y is between f(a) and f(b) then y=f© for some c in [a,b]

intermediate value property

a function has this if it never taking on two values without taking on all the values between

the average rate of change

of a quantity of a period of time is the amount of change divided by the time is takes. it is also the slope of the secant line.

defining tangents

1)calculate the slope of the secant through p and a point q on the curve

2) find the limiting value of the secant slope (if it exists) as q approaches p along the curve

3) we define the slope of the curve at p to be this number and define the tangent to the curve at point p to be the line through p with this slope

slope of the curve

y=f(x) at the point p(a,f(x)) is the number m=limh→ 0 f(a+h)-f(a)/h

Tangent to the curve

At p is the line through p with this slope

Difference quotient of Fa Ta

F(t+h)-f(t)/h

Normal line

To a curve at a point is the line perpendicular to the tangent at that point

Slope of the secant line

Slope between the intersection points

Instantaneous rate of change

Change that occurred at a single point, slope of a curve at a point, derivative of a point, slope of a tangent line at that point

Derivative

Of a function f with respect to the variable c is

F(x)=lim h→0 f(x+h)-f(x)/h

differentiable function

Y’=y prime

F’(x)=f prime or x

Dy/Dx= derivative of y with respect to x

Df/Dx= derivative of f with respect to x

D/dx f(x)= derivative of f at x