FLASHCARDS - AP CALCULUS BC

Derivative of g(x) if f(x) and g(x) are inverses

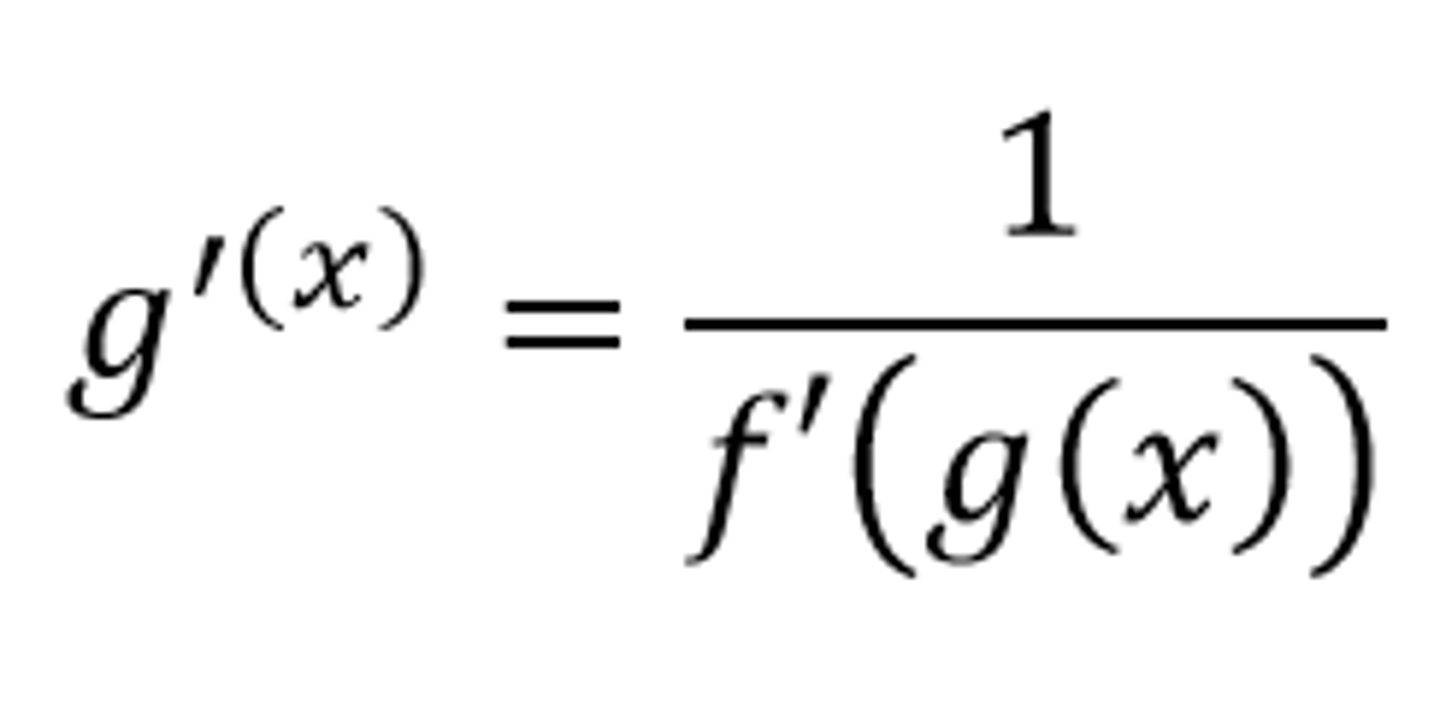
Average value of f(x) on [a, b]

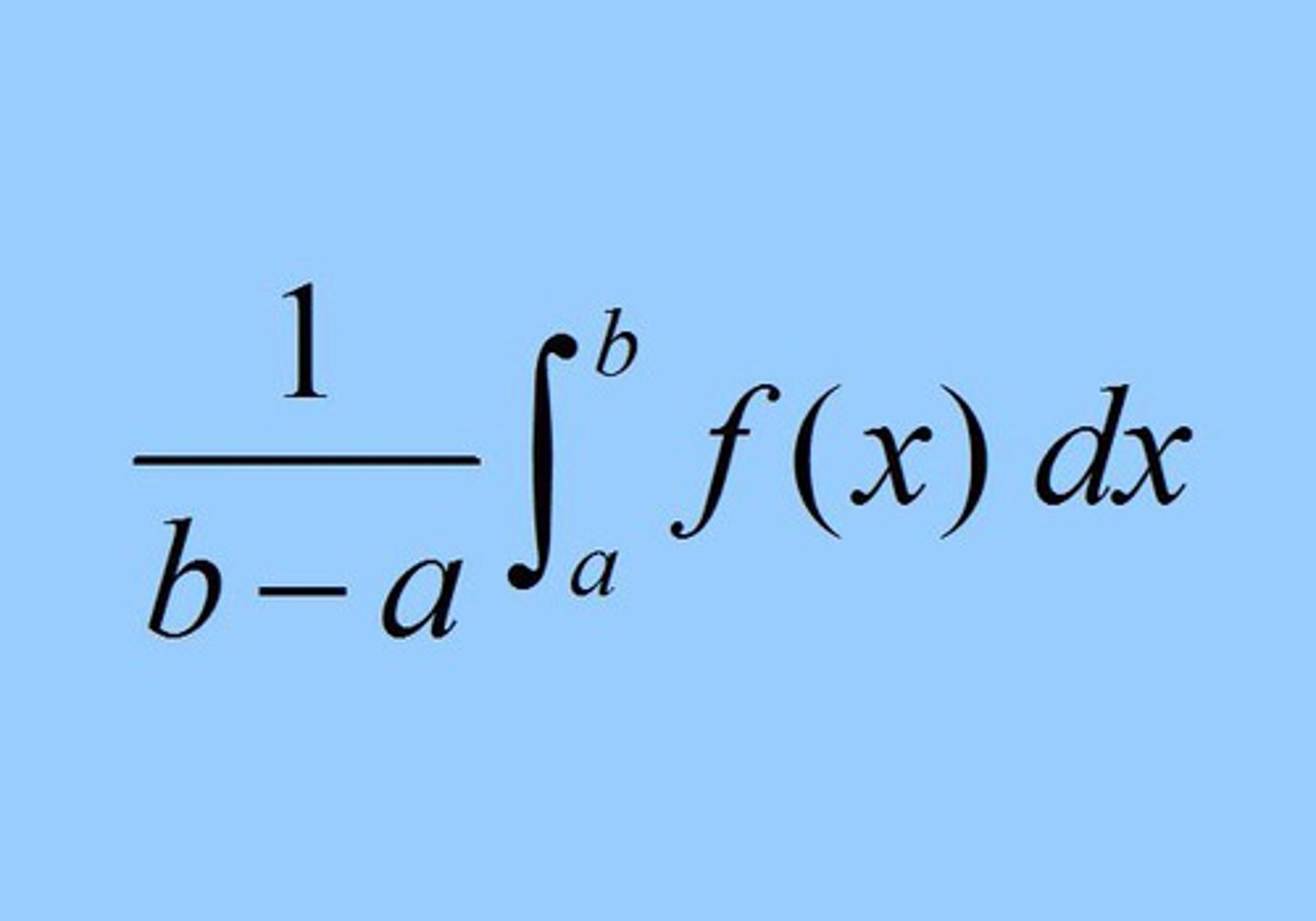
Arc Length - Parametric

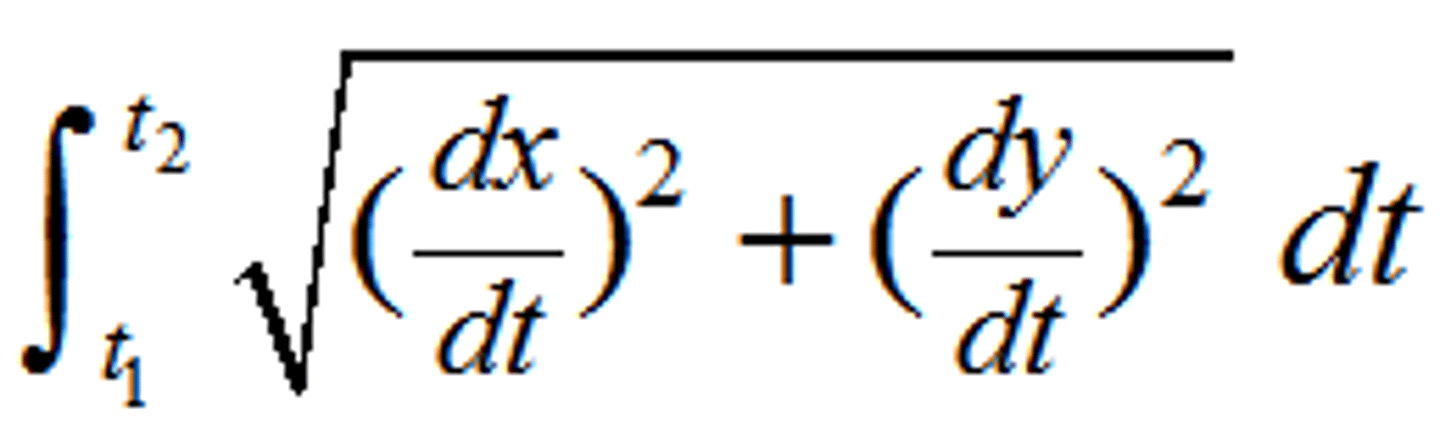
Integral of sec(x)tan(x)dx

sec(x) + C

Root Test

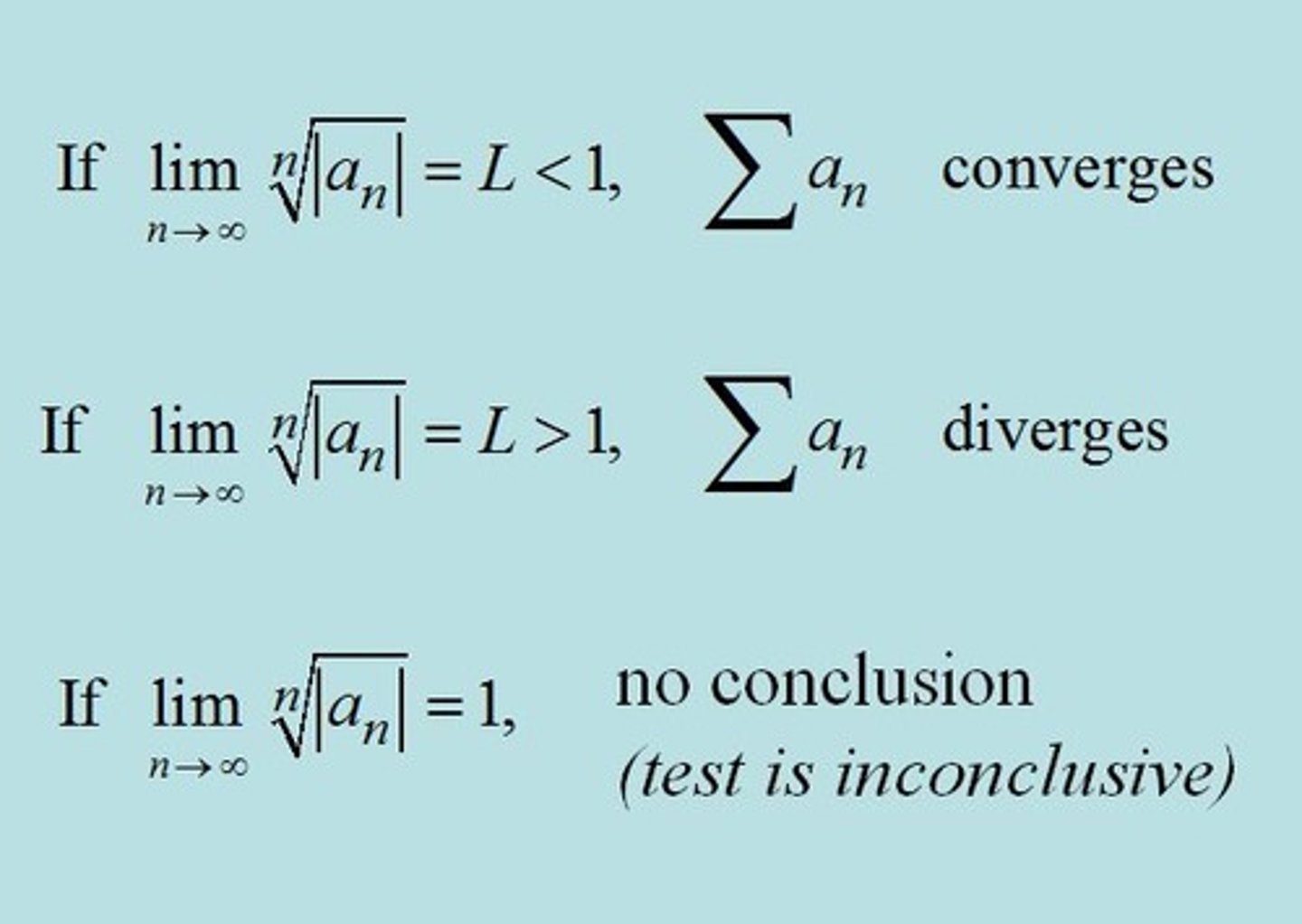
Given a graph of f'(x), when is f(x) INCREASING?

When f'(x) is POSITIVE

Direct Comparison Test

Less than a convergent converges; Greater than a divergent diverges

Average Rate of Change of f(x) on (a, b)

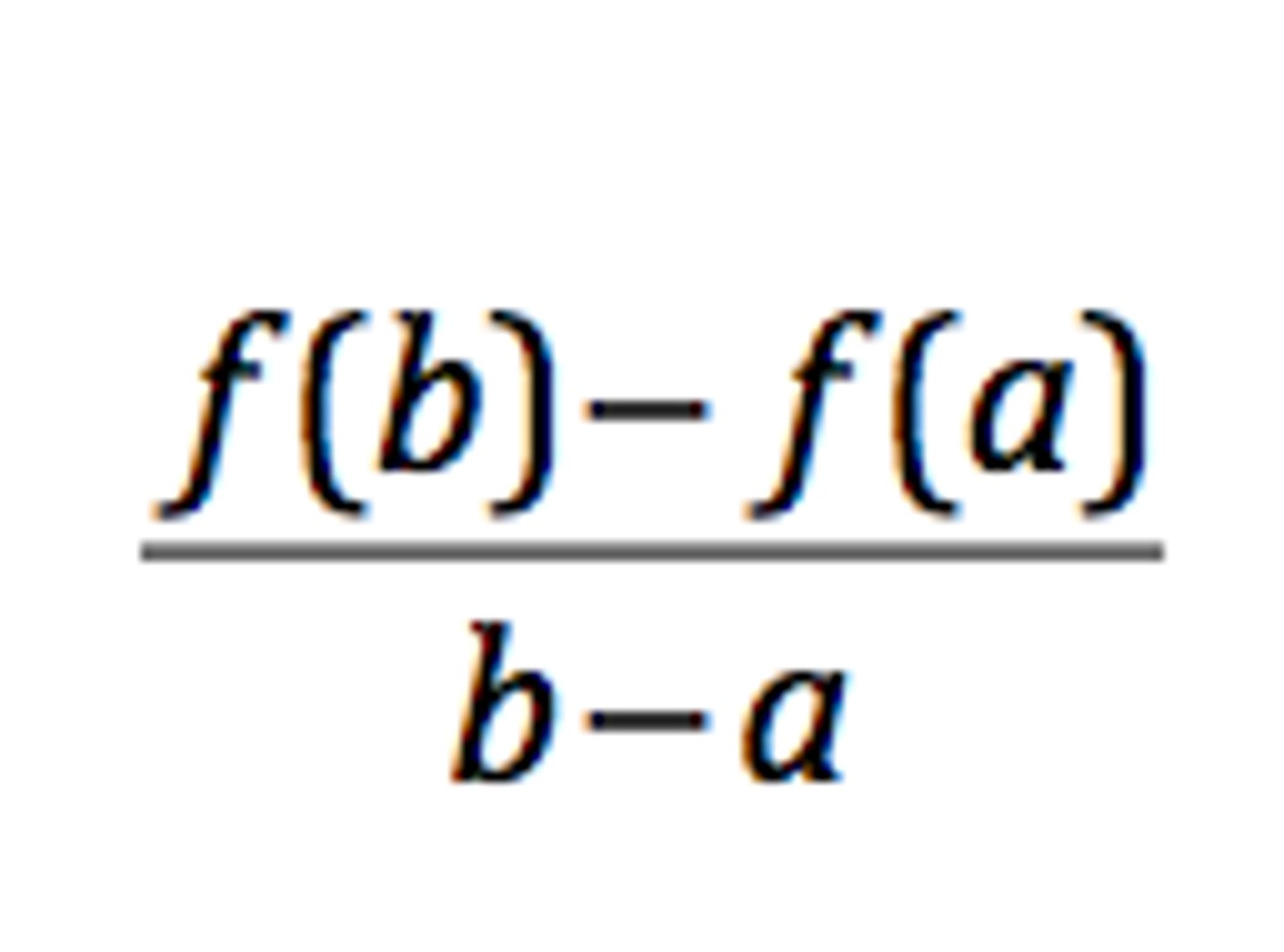
Integral of sin(x)dx

-cos(x)+C

1+x+x^2/2!+x^3/3!...

e^x

Area enclosed by a Polar Curve (from α to ß)

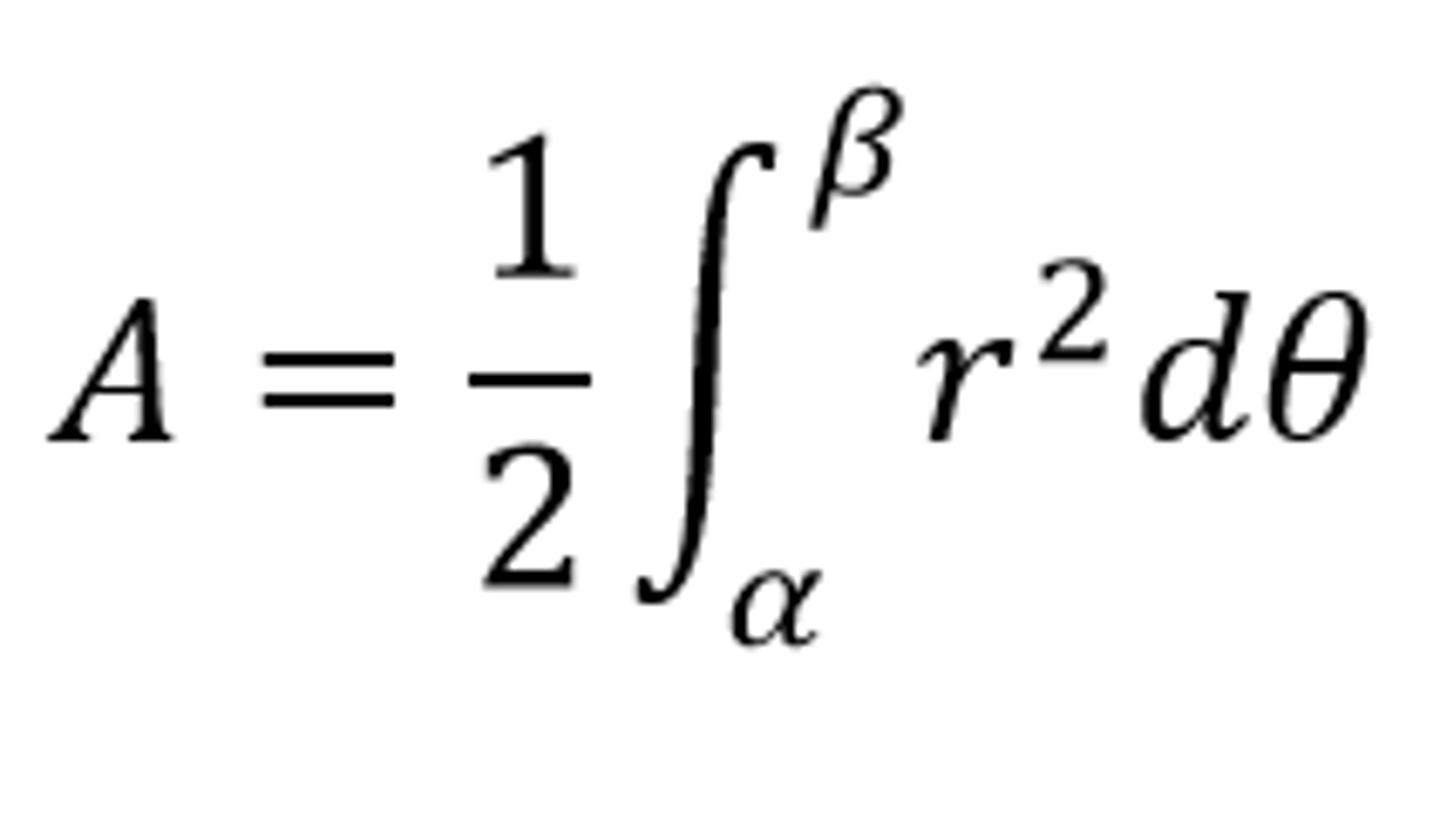
Integral of dx/x

ln|x| + C

Derivative of tan(x)

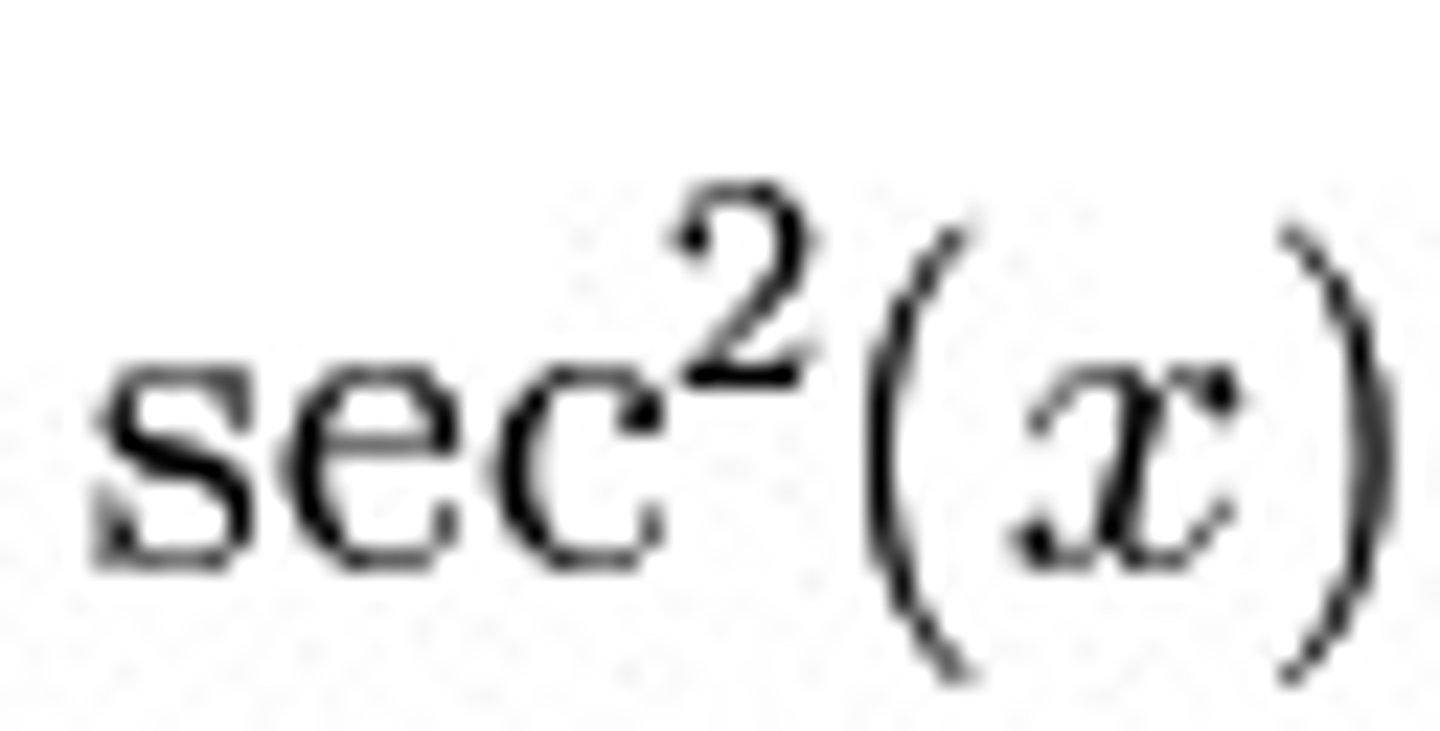
Euler's Method

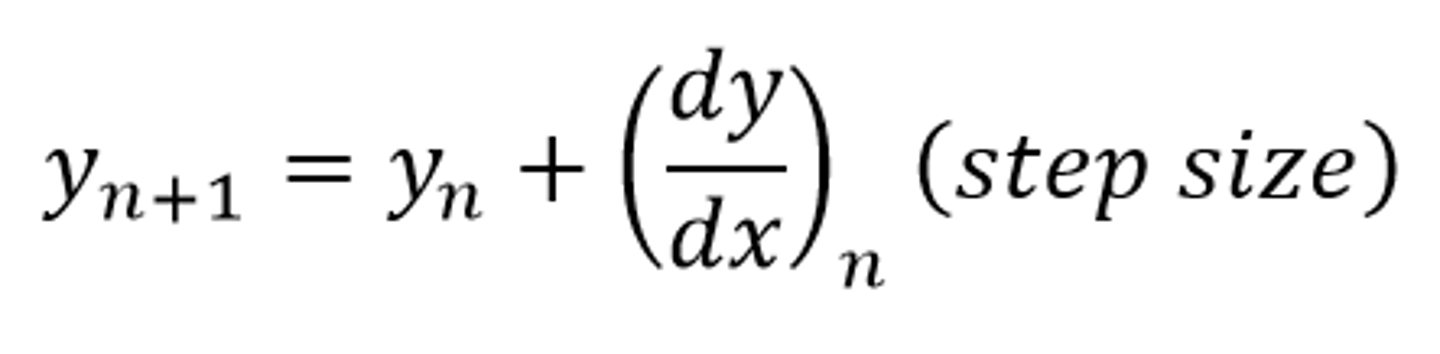
Parametrics - Speed

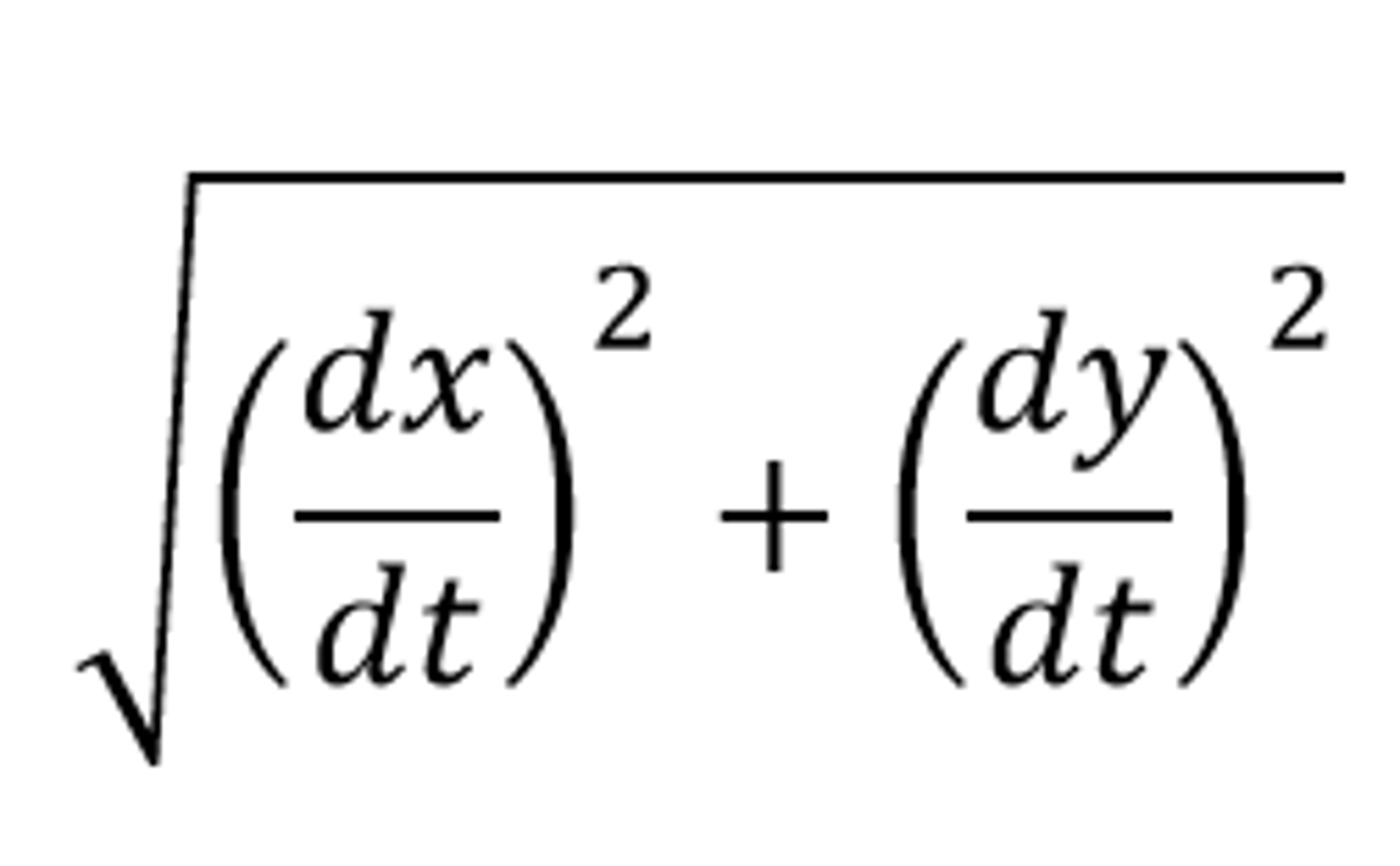
Integral of dx/sqrt(1-x^2)

arcsin(x)

Arc Length - Rectangular

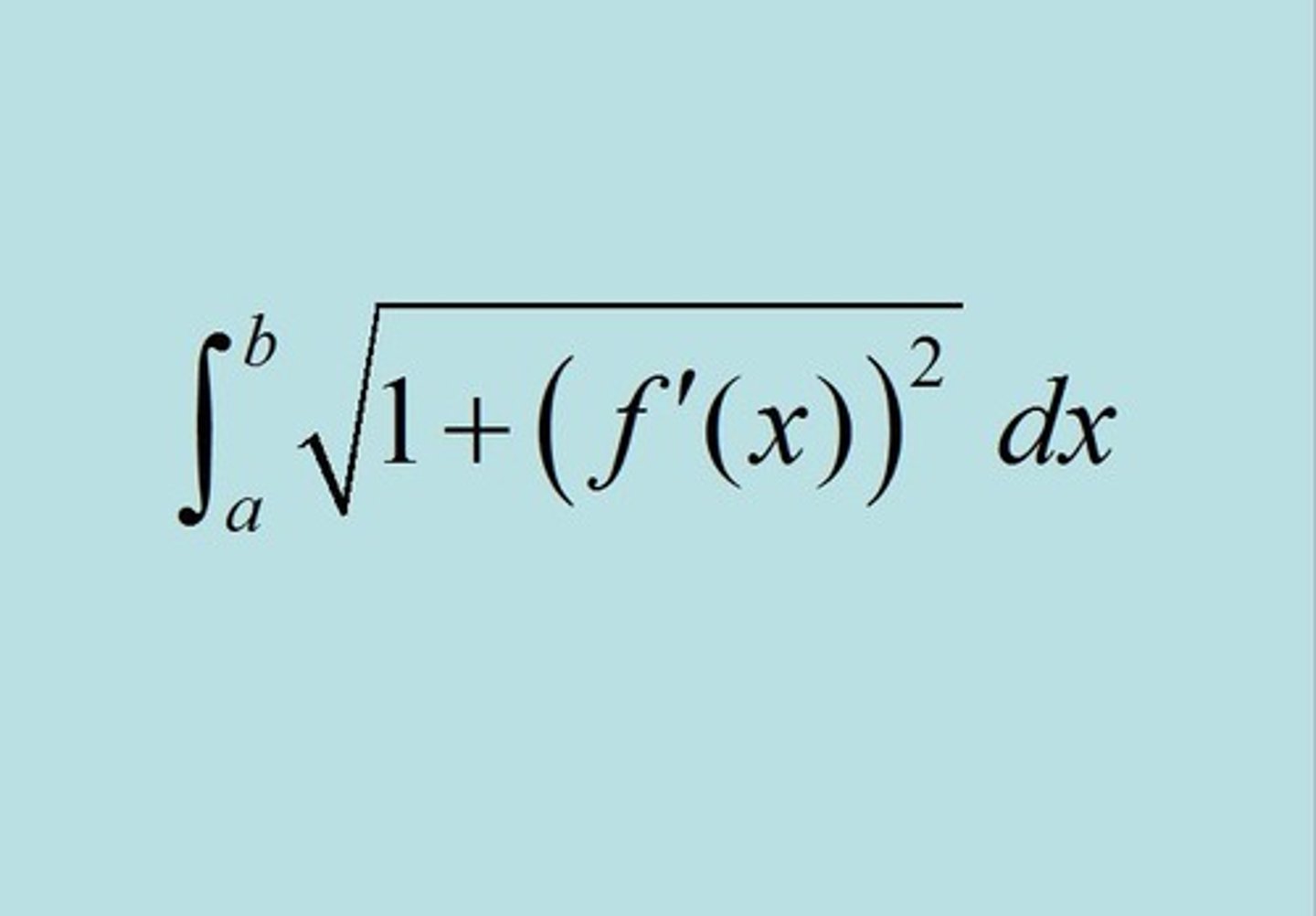
Converting from POLAR to RECTANGULAR

x=rcos(θ) y=rsin(θ)

Maclaurin Series for sin(x)

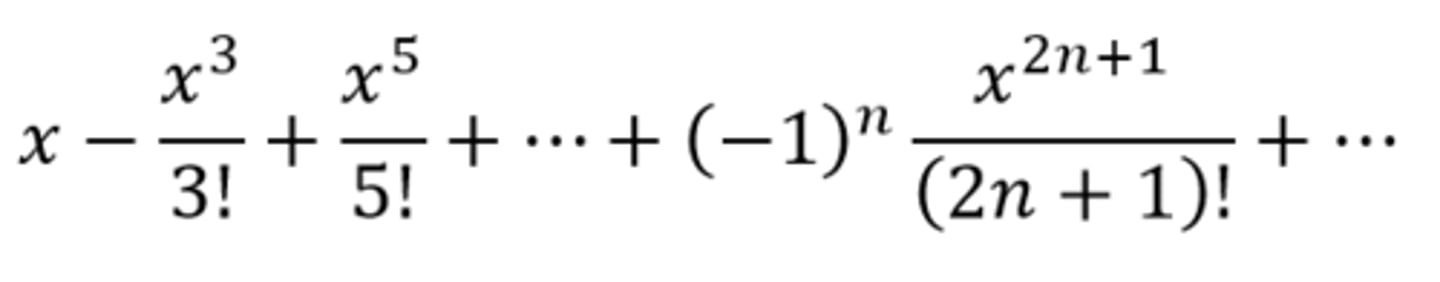
Maclaurin Series for 1/(1-x)

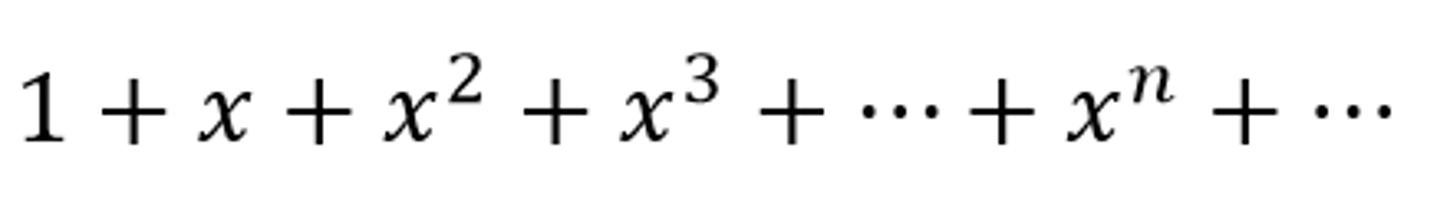
In the Logistic Model, for what value of P is P growing the fastest? (is dP/dt a maximum)

P = M/2

Derivative of arcsin(x)

1/√(1-x^2 )

Parametrics - Slope of Path

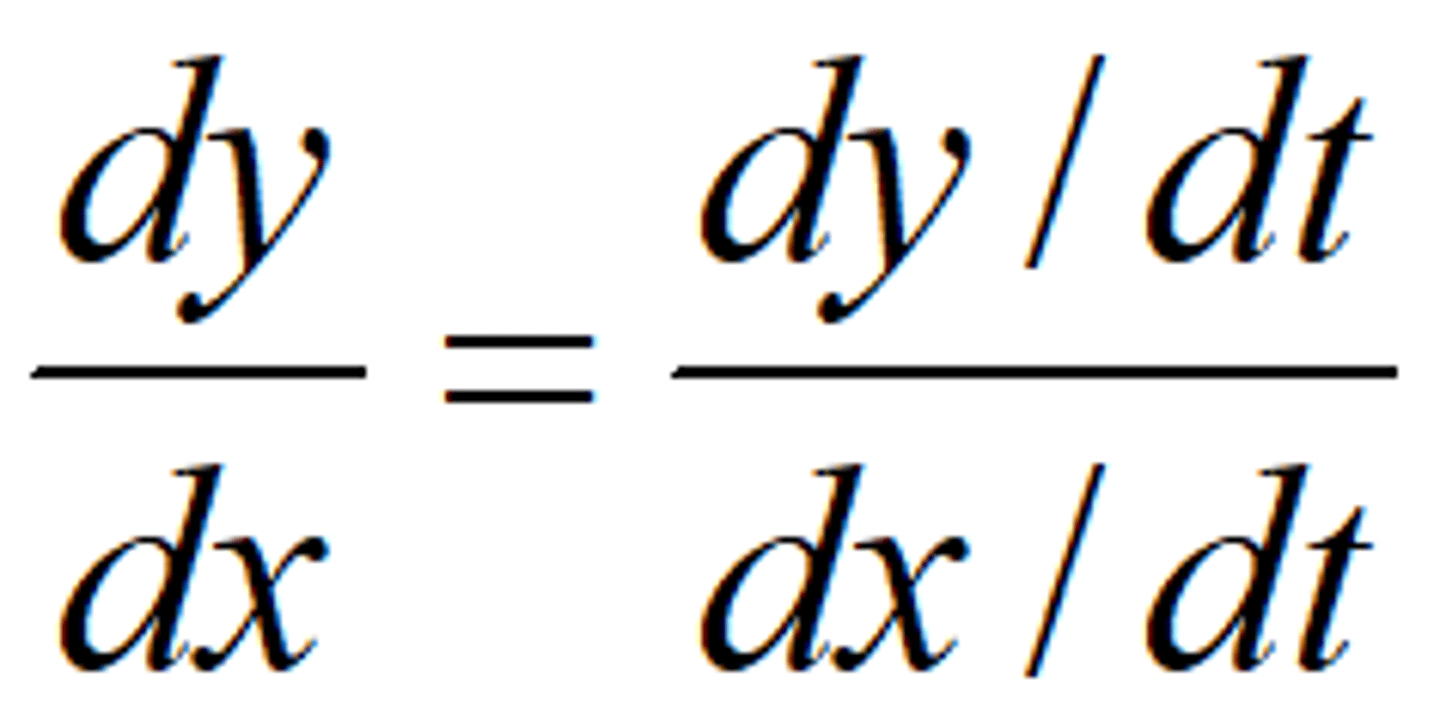
Derivative of sec(x)

Sec(x)tan(x)

Given a graph of f'(x), when does f(x) have a POINT OF INFLECTION?

When f'(x) has a min/max (or horizontal tangent)

Describe the nth term test for divergence

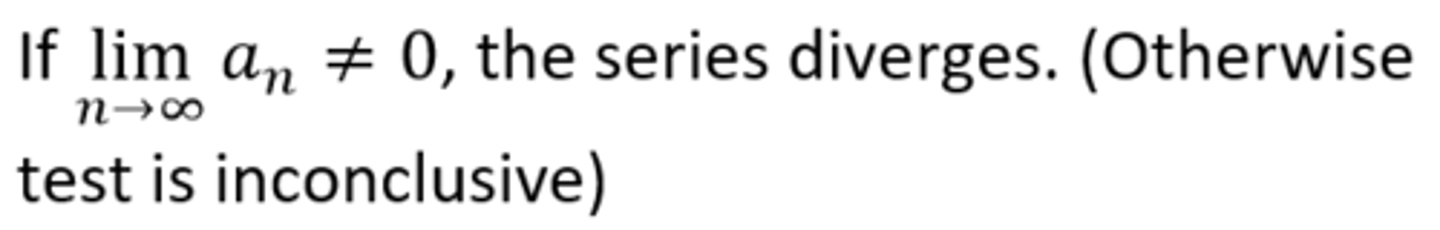
Geometric Series Test (and Sum)

If |r|<1, converges to initial/(1-r). If |r|≥1, diverges

Limit Comparison Test

if the limit as n approaches infinity of (given series/chosen series) is >0 and finite, the two series will DO THE SAME THING

Integral of sec^2(x)

tan(x)+C

Parametric Equations - Acceleration Vector

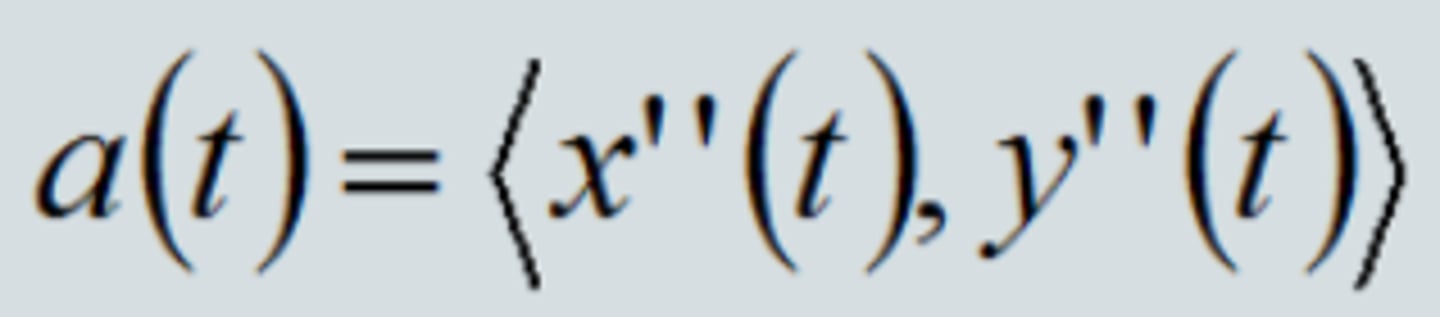
General formula of a Taylor Series

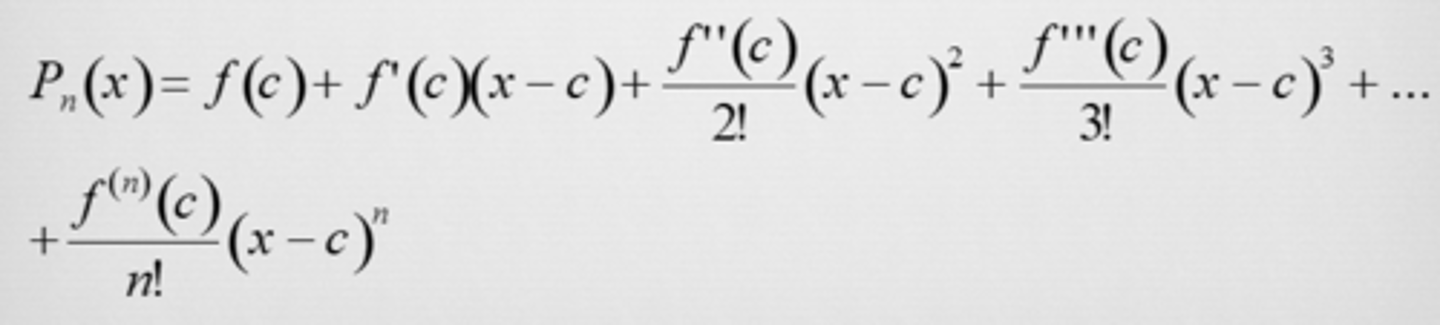
Parametrics - Velocity Vector

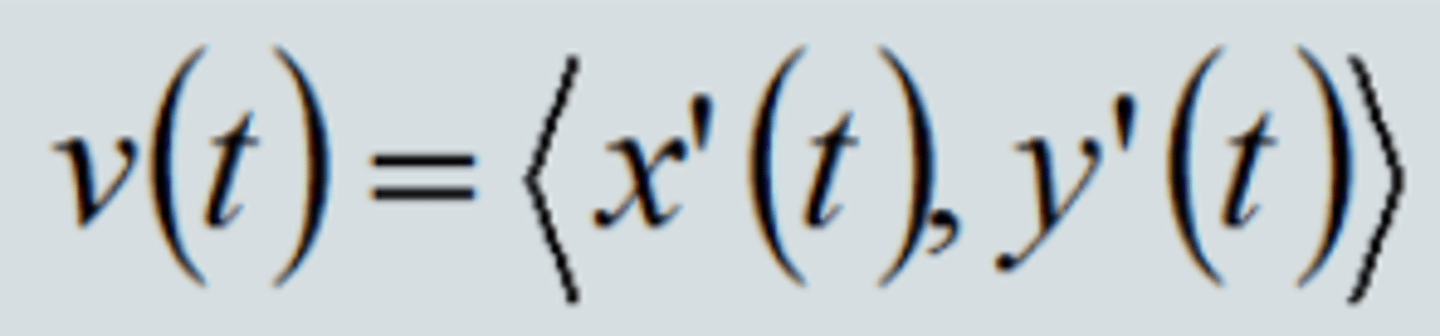
LaGrange Error Bound

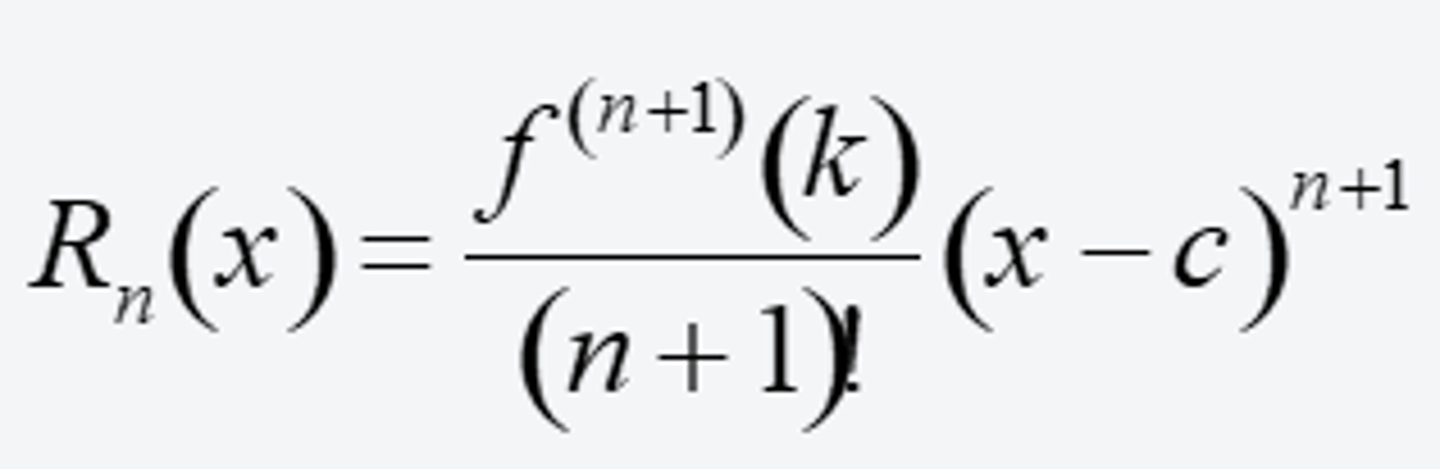
Given a graph of f'(x), when is f(x) CONCAVE UP

When f'(x) is INCREASING

Alternating Series Error bound

|error|<1st neglected term

Slope of a Polar Curve

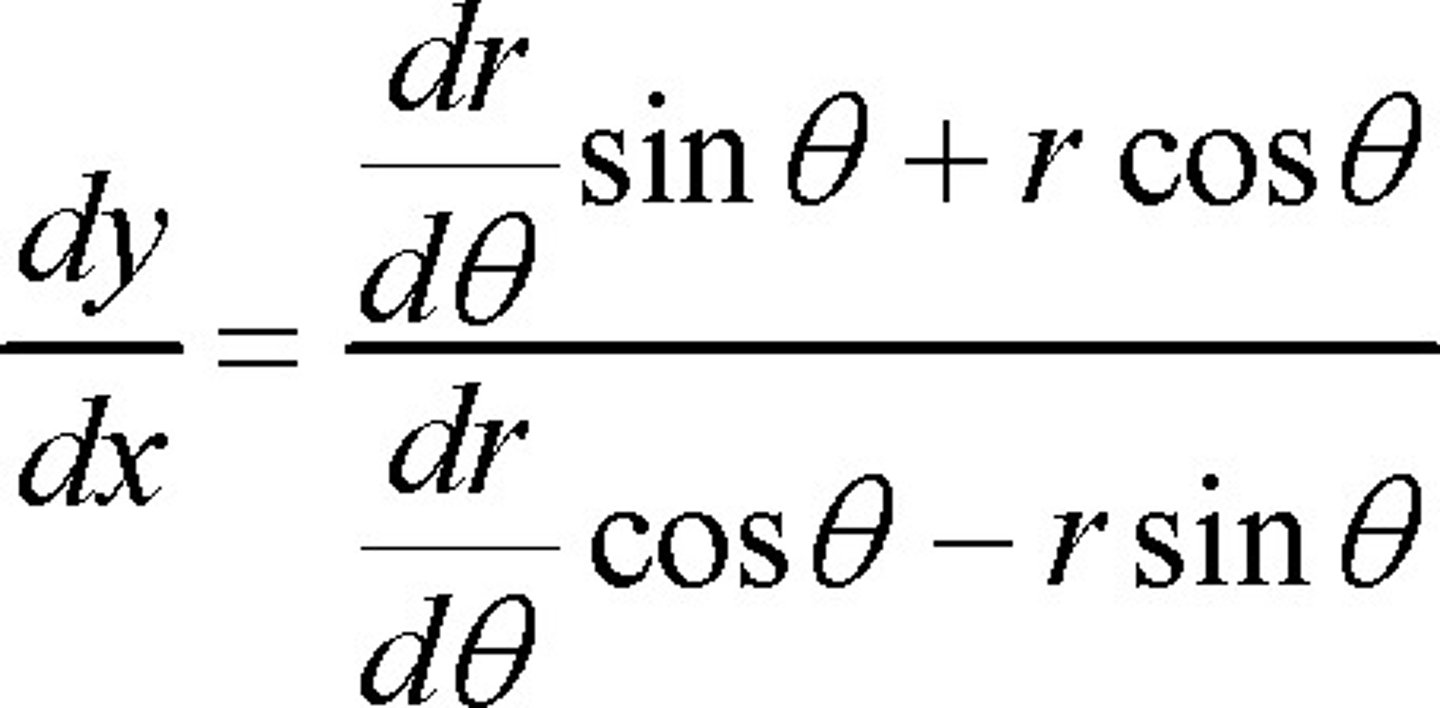
1-x^2/2!+x^4/4!+...

cos(x)

Alternating Series Test (3 conditions)

alternates, limit goes to 0, a_n+1 < a_n

integral of cos(x)dx

sin(x)

Derivative of sin(x)

cos(x)

Ratio Test

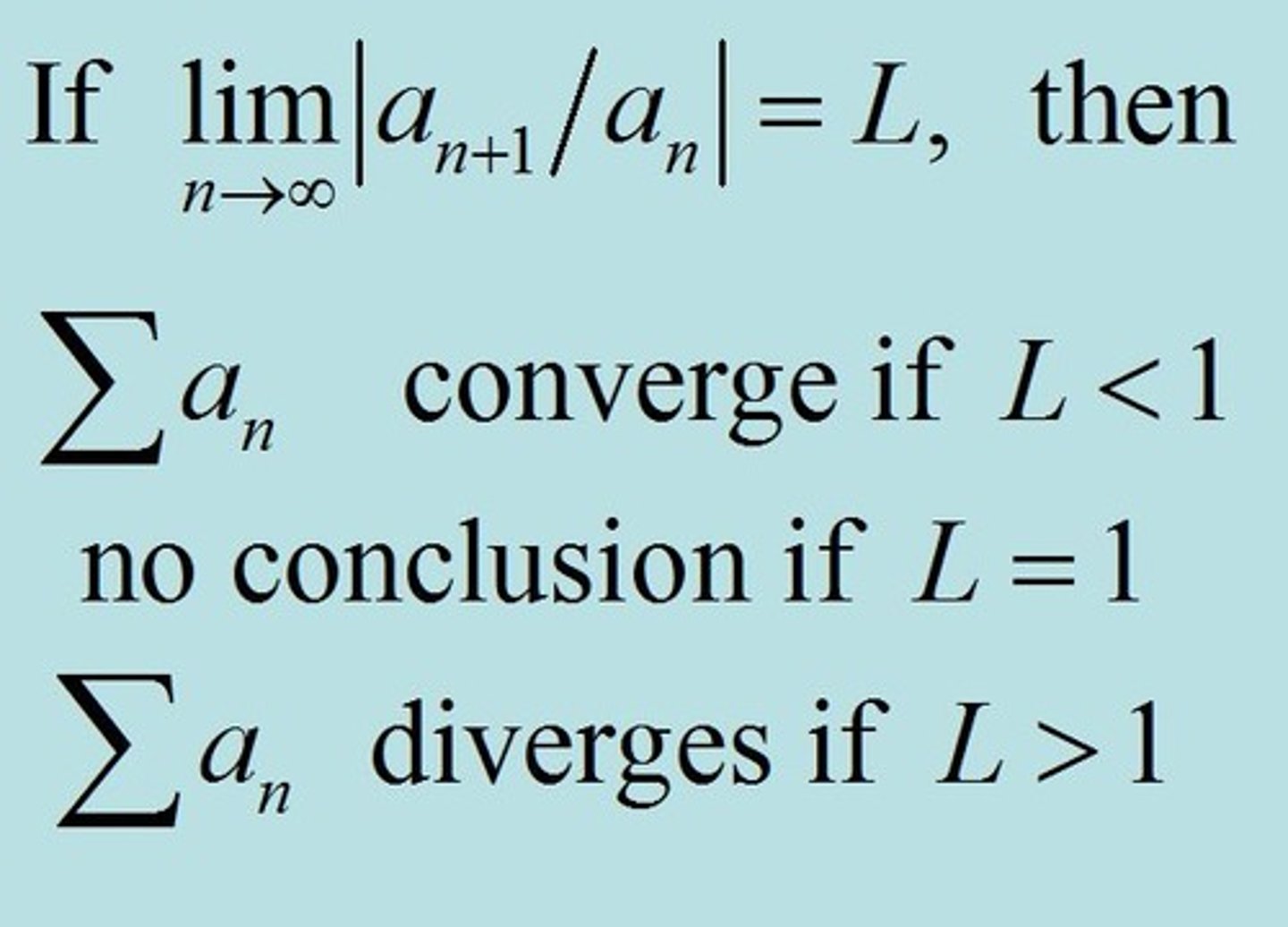
x-x^3/3!+x^5/5!+...

sin(x)

Given a graph of f'(x), when does f(x) have a min/max?

When f'(x) changes from negative to positive, positive to negative

Maclaurin Series for e^x

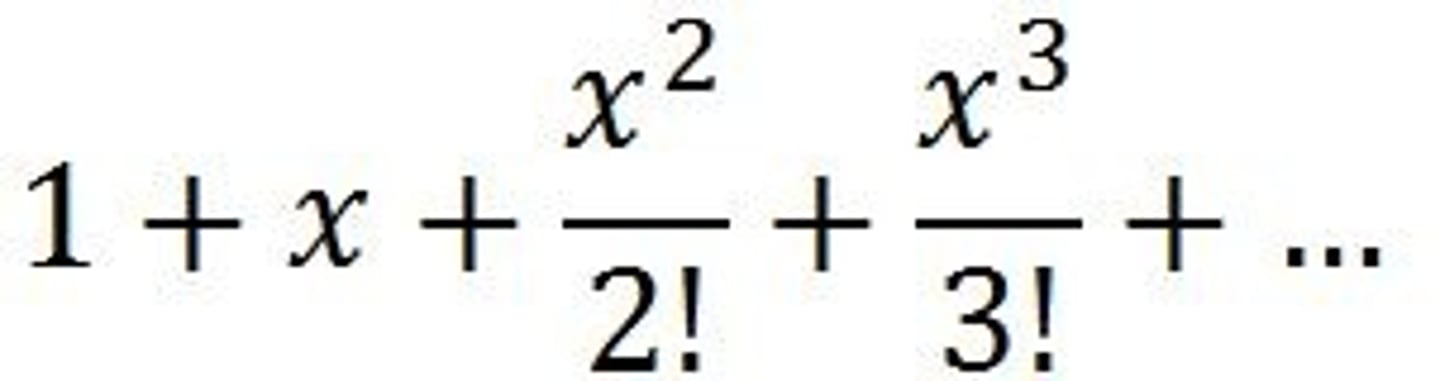
Logistic Model: what is the limit as t goes to infinity of P(t)?

M

P-series (sum of 1/n^p)

Converges if p>1, Diverges if p less than or equal to 1

Integral of dx/(1+x^2)

arctan(x)+C

Derivative of arctan(x)

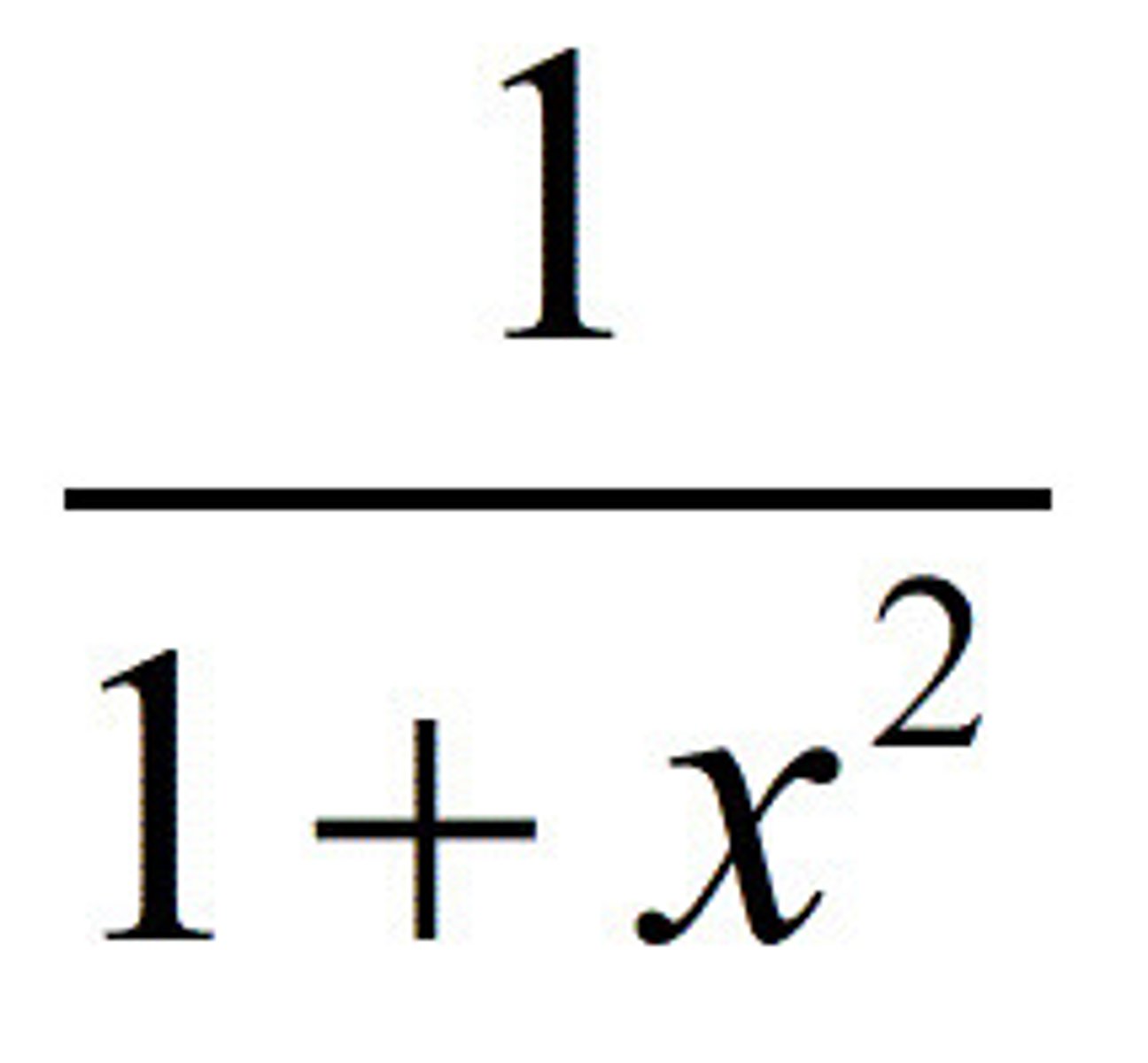
SECOND DERIVATIVE of y with respect to x for Parametrics

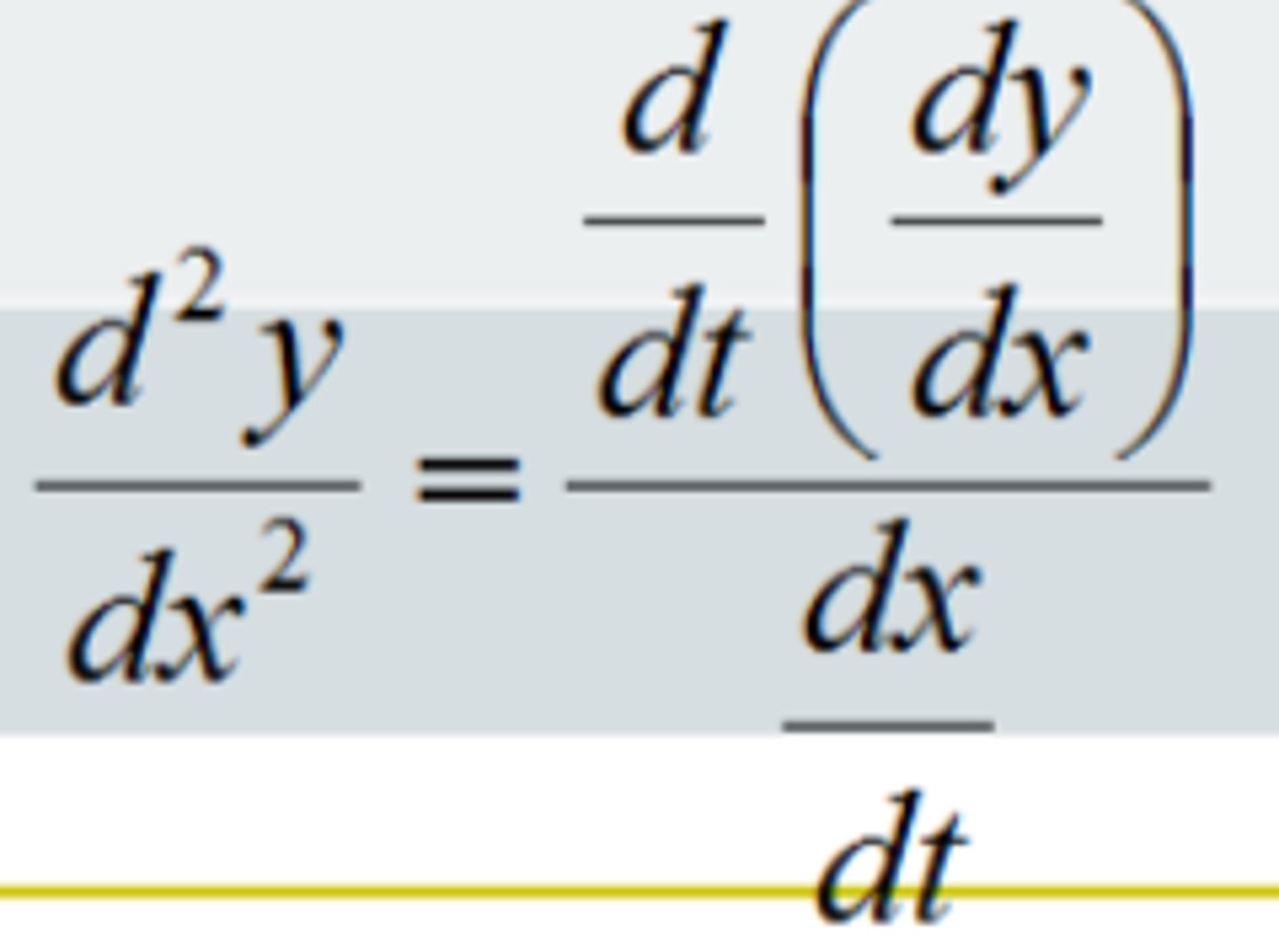
1+x+x^2+x^3+....

1/(1-x)

Logistic Model (both forms dP/dt = )

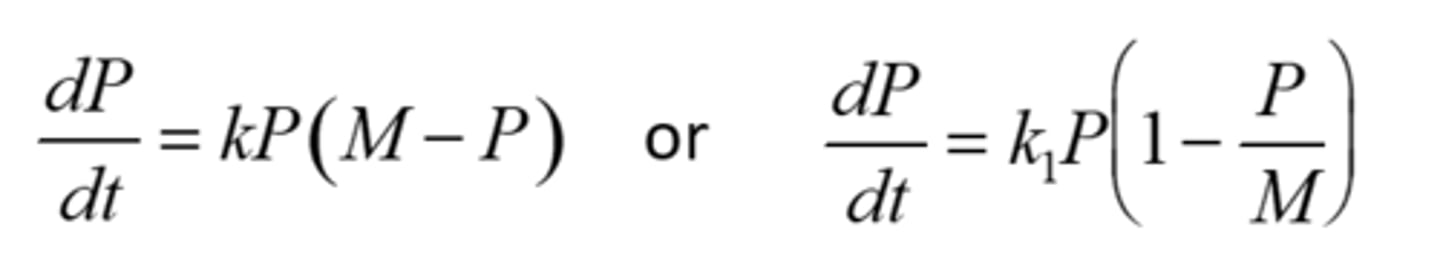
Parametrics - when is the particle NOT MOVING?

both dx/dt=0 and dy/dt=0

Maclaurin Series for cos(x)

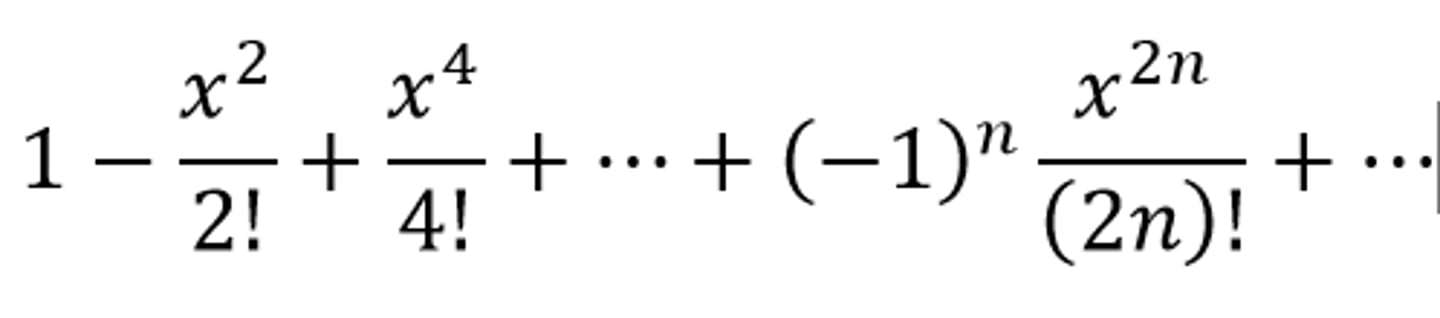
Derivative of cos(x)

-sin(x)