Logic And Reasoning

Tautology

when a compound proposition is always true in its truth table

Contradiction

when a compound proposition is always false in its truth table

Contingency

when a compound proposition is neither a tautology or a contradiction

Logically Equivalent (Condition for something to be qualified as such)

Two compound propositions, P and Q, are said to be logically equivalent if and only if the proposition P↔Q is a tautology

Example: ‘P ≡ Q’.  For example,(p→q) ≡ (¬p∨q), and p⊕q ≡(p∨q)∧¬(p∧q)

Principle of Explosion

If the premises of a proposition includes a contradiction, any statement can be proven from it

Conditional Statement

If, then. Implication of something. Implication, conditional.

p→q. p is the hypothesis or antecedent, q is the conclusion or consequent.

If p→q is true, then p is sufficient for q.

logically equivalent to ¬p∨q

Converse

q→p is the converse of p→q

Contrapositive

¬q→¬p is called the contrapositive of p→q

Inverse

¬p→¬q is the inverse of p→q

Biconditional Statement

If and only if.

could also be expressed as ‘if p then q, and conversely’ which translates to p↔q is logically equivalent to (p→q)∧(q→p)

can be expressed as (¬p∨q)∧(¬q∨p)

Exclusive Or

Symbol: ⊕

stands for “p or q, but not both”

Order Of Operations (5 symbols)

Boolean Algebra Laws (9)

Duality

given any tautology that uses only the operators ∧,∨, and ¬, another tautology can be obtained from it by interchanging ∧ with ∨ and T with F. (The reason why the boolean algebra laws come in pairs)
example: p ∨ ¬p≡ T

becomes: p ∧ ¬p≡ F

Simple Term

either a propositional variable or the negation of a propositional variable Example: p, ¬q

Compound Proposition

A proposition made up of smaller propositions

Example: (¬p∨q)∧(¬q∨p)

Disjunctive Normal Form (DNF)

When a compound proposition is organized in a way that it is a disjunction of conjunctions of simple terms. Each propositional variable occurs at most once in each conjunction and each conjunction occurs at most once in the disjunction.

Disjunction

Or statement. ∨ symbol

Conjunction

And statement. ∧ symbol

Karnaugh Map + Rules

A method to simplify propositions into a minimal sum of products (which is a fancy way of saying DNF form)

Predicate

a kind of incomplete proposition, which becomes a proposition when it is applied to some entity.

example: In the proposition “the rose is red”, the predicate is “is red”. By itself,‘is red’ is not a proposition

Entity

some specific, identifiable thing to which a predicate can be applied

example: if P means “is red” and a is “the rose”, P is the predicate while a is the entity

One-Place predicate

A predicate that can have one collection of entities assigned to it. (assign one entity to it, but has to be a part of a domain of discourse that works for the predicate)

Example: In the proposition “John loves Mary”, “loves” is a two-place predicate. Besides John and Mary, it could be applied to other pairs of entities (any other 2 people)

Domain of discourse

The set of entities that that can fit in a description.

Example: owns(a,b). domain of discourse of “a” can be humans, and domain of discourse of “b” can be any object.

Propositions

When a predicate is applied to an entity

Quantifiers

Words like all, no, some, and every

Universal Quantifier

∀ symbol means, “for all” of something

Existential Quantifier

∃ symbol means there exists an entity for which…

Open statement

An expression that contains one or more entity variables, which becomes a proposition when entities are substituted for the variables. It has “slots” that need to be filled in.

Example: x owns y (we dont know what x and y are at this point)

Free variables

The variables in an open statement that will have to be substituted by an entity. In ∃x(P(x)), x is bound to the ∃ of P. in P(x), it is free as it is not bound to a quantity.

Tarski’s world

DeMorgan’s Predicate Logic Laws (4)

Premise

A proposition that is known to be true or that has been accepted to be true for the sake of the argument

Argument

A claim that a certain conclusion follows from a given set of premises. An argument is valid if the conclusion follows logically from the premises. To disprove it, give a counterexample.

Example: If today is Tuesday, then this is Belgium. Today is Tuesday. Therefore this is Belgium.

Symbol for P→Q is a tautology and that P logically implies Q.

P⇒Q

Laws of Deduction. (3)

Modus Ponens: Statement is: If p is true, then q is true. We know that p is true, so q must be true.

Modus Tollens: Statement is: If p is true, then q is true. We know that q is not true, so p can not be true.

Law of Syllogism: Statement is: If p is true, then q is true. We know that if q is true, r is true. So, if p is true then r is also true.

How to specify there is only one of something in predicate logic. (There is only one detective that is not trustworthy)

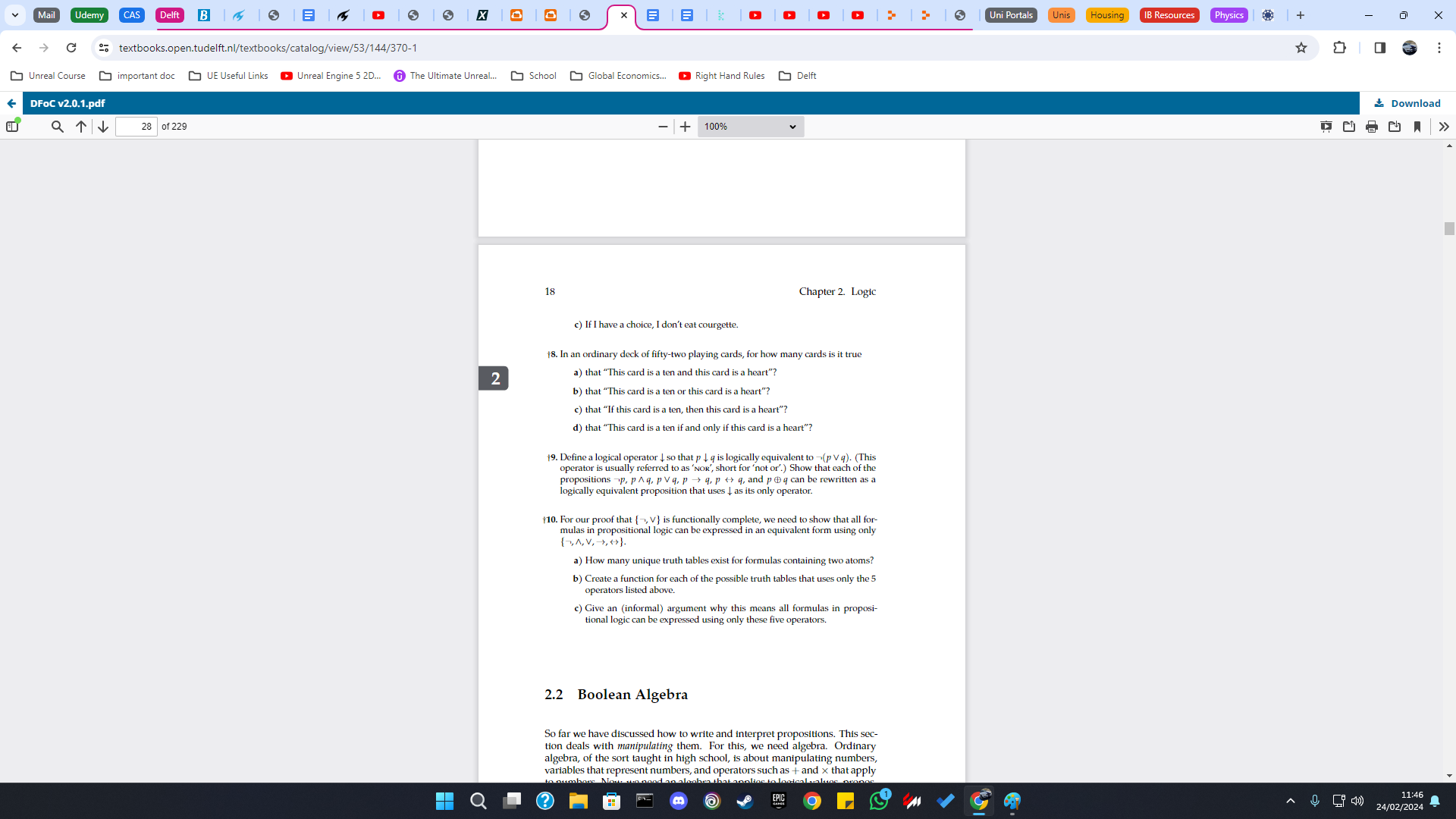
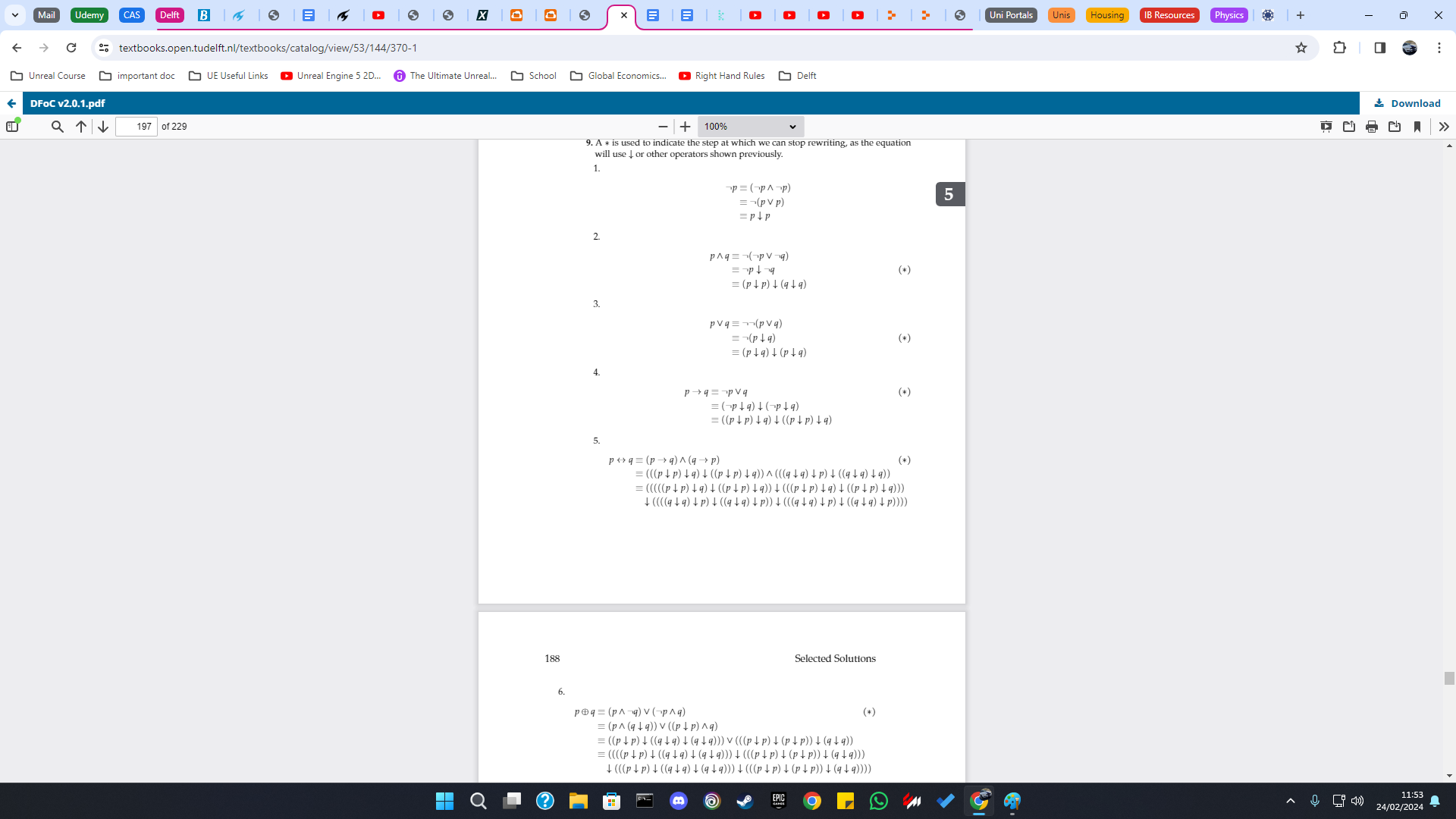
2.1 Hard Questions

8.a: 1 card (ten of hearts), 8.b: 16 cards, 8.c: Only 3 cards that dont satisfy so 49 do, 8.d: 37 cards (12 hearts that are not a 10, 3 cards that are 10s but not a heart do not satisfy), 10: (2²)^n (n=#atoms)