ТЗ(3)

Наведіть змістовне формулювання ТЗ

Наведіть змістовне формулювання ТЗ

Транспортна задача — це задача оптимізації, яка полягає у визначенні найекономічнішого способу перевезення товарів від кількох постачальників до кількох споживачів. Вона враховує обмеження на запаси товарів у постачальників, потреби споживачів і витрати на транспортування між кожною парою 'постачальник-споживач'. Метою є мінімізація загальних витрат на транспортування, при цьому потрібно задовольнити всі потреби споживачів і не перевищити запаси постачальників.

Наведіть формальну постановку ТЗ

Вхідні дані:

• 𝑚m постачальників із запасами 𝑎𝑖ai​ (для 𝑖=1,2,...,𝑚i=1,2,...,m).

• 𝑛n споживачів із потребами 𝑏𝑗bj​ (для 𝑗=1,2,...,𝑛j=1,2,...,n).

• Матриця витрат на транспортування 𝐶=[𝑐𝑖𝑗]C=[cij​], де 𝑐𝑖𝑗cij​ — вартість перевезення одиниці товару від постачальника 𝑖i до споживача 𝑗j.

Ціль:

Мінімізувати загальні витрати на транспортування: 𝑍=∑𝑖=1𝑚∑𝑗=1𝑛𝑐𝑖𝑗𝑥𝑖𝑗Z=∑i=1m​∑j=1n​cij​xij​

Обмеження:

1. Кількість товару, відправлена від кожного постачальника: ∑𝑗=1𝑛𝑥𝑖𝑗≤𝑎𝑖∀𝑖∑j=1n​xij​≤ai​∀i

2. Кількість товару, отримана кожним споживачем: ∑𝑖=1𝑚𝑥𝑖𝑗=𝑏𝑗∀𝑗∑i=1m​xij​=bj​∀j

3. Не від'ємність кількості товару: 𝑥𝑖𝑗≥0∀𝑖,𝑗xij​≥0∀i,j

Мета:

Знайти матрицю перевезень 𝑋=[𝑥𝑖𝑗]X=[xij​], яка мінімізує 𝑍Z і задовольняє всі обмеження.

Що є основними обмженнями ТЗ?

Основними обмеженнями транспортної задачі (ТЗ) є:

1. Обмеження запасів (постачальників): Кількість товару, яку може відправити кожен постачальник, обмежена його запасом.

2. Обмеження потреб (споживачів): Кількість товару, яку кожен споживач очікує отримати, обмежена його потребою.

3. Неот'ємність: Кількість перевезеного товару не може бути від'ємною, оскільки це фізично неможливо.

Що таке умова балансу

Умова балансу

Дайте означення відкритої тз

ТЗ де порушена умова балансу

Дайте означення закритої тз

ТЗ де виконується умова балансу

як звести закриту тз до відкритої

Перетворення закритої транспортної задачі (ТЗ) на відкриту може здійснюватися за допомогою додавання фіктивного постачальника або споживача. Цей підхід стає необхідним, коли загальні обсяги постачання не дорівнюють загальним обсягам попиту.

Наведіть основні властивості ТЗ

Кожну змінну xij ТЗ налічує система основних обмежень лише двічі
Елементи матриці основних обмежень – це нулі та одиниці. Кожен стовпець матриці має лише дві одиниці, решта елементів – нулі. Кожен рядок матриці має n або m одиниць, решта елементів – нулі.

Сформулюйте теорему про ранг матриці основних обмежень ТЗ

∑xij = a =1 ; i =1,m ,
∑x = b =1 , j =1, n .

Доведіть теорему про ранг матриці основних обмежень ТЗ

доведення

Сформулюйте і доведіть необхідну умову існування розвязків ТЗ

Для існування розв'язку транспортної задачі необхідно, щоб загальний обсяг постачання дорівнював загальному обсягу попиту.

Формулювання:

Нехай 𝑎𝑖ai​ — запас товару у 𝑖i-го постачальника (для 𝑖=1,2,...,𝑚i=1,2,...,m), а 𝑏𝑗bj​ — потреба в товарі у 𝑗j-го споживача (для 𝑗=1,2,...,𝑛j=1,2,...,n).

Необхідна умова: ∑𝑖=1𝑚𝑎𝑖=∑𝑗=1𝑛𝑏𝑗∑i=1m​ai​=∑j=1n​bj​

Сформулюйте і доведіть достатню умову існування розвязків ТЗ

Для існування розв'язку транспортної задачі достатньо, щоб загальний обсяг постачання дорівнював загальному обсягу попиту:

∑𝑖=1𝑚𝑎𝑖=∑𝑗=1𝑛𝑏𝑗∑i=1m​ai​=∑j=1n​bj​

де 𝑎𝑖ai​ — запас товару у 𝑖i-го постачальника (для 𝑖=1,2,...,𝑚i=1,2,...,m), а 𝑏𝑗bj​ — потреба в товарі у 𝑗j-го споживача (для 𝑗=1,2,...,𝑛j=1,2,...,n).

Що таке опорний план ТЗ? Що таке вироджений невироджений оп?

серед m + n лінійно залежних рівнянь системи (4.2), (4.3) з mn невідомими можна виокремити підсистеми, які містять m + n –1 лінійно незалежних рівнянь. Виокремлюючи у таких підсистемах базисні невідомі, можна знайти базисні допустимі розв’язки (або опорні плани) Xоп системи (4.2) – (4.4). Кожен опорний план має не більше m + n –1 ненульових (додатних) компонент та не менше mn – (m + n – 1) = = (m –1 )(n –1) нульових.

Опорний план ТЗ (вектор Xоп ), який містить m + n –1 ненульових компонент, називають невиродженим. У виродженого опорного плану кількість ненульових компонент є меншою за m + n –1.

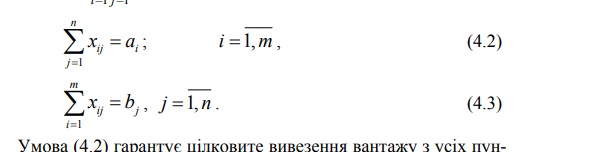
Дайте означення ланцюжка клітинок. Що таке цикл?

Ланцюжок клітинок у контексті транспортної задачі - це послідовність клітинок таблиці транспортної задачі, в якій кожна клітинка з'єднана з попередньою і наступною по рядку або по стовпцю. Ланцюжок використовується для переміщення товарів між різними клітинками, щоб зберегти рівновагу в задачі і забезпечити оптимальне рішення.

Цикл у таблиці транспортної задачі - це замкнутий ланцюжок клітинок, який починається і закінчується в одній і тій самій клітинці. Цикли є важливими для оптимізації плану перевезень, оскільки вони дозволяють коригувати план, переміщуючи товар по циклу без зміни загальних запасів та потреб. Цикли використовуються для корекції початкового опорного плану з метою покращення (зниження) вартості перевезень.

Опишіть алгоритм методу викреслювання

Алгоритм методу викреслювання:

1. Переглядаємо усі рядки таблиці Т і викреслюємо ті з них, які не мають елементів R або мають тільки один елемент R.

2. Переглядаємо усі стовпці таблиці Т і викреслюємо ті з них, які не мають елементів R або мають тільки один елемент R. Раніше викреслені елементи до уваги не беруть.

Повторюємо кроки 1 – 2. Після скінченної кількості кроків процес викреслювання завершиться

Сформулюйте і доведіть необхідну умову існування ОП

Наслідок 4.1 (з теореми 4.3). Для того, щоб деякий план у таблиці перевезень був опорним, необхідно і достатньо, щоб із базисних клітинок не можна було скласти замкнутий ланцюжок (іншими словами: з комунікацій, які відповідають базисним клітинкам, не можна було скласти замкнутий маршрут).

Теорема 4.3. Система векторів перевезень Е лінійно незалежна тоді і тільки тоді, коли з клітин, які відповідають векторам системи Е, не можна скласти замкнутий ланцюжок (цикл).

Сформулюйте і доведіть достатню умову існування ОП

Наслідок 4.1 (з теореми 4.3). Для того, щоб деякий план у таблиці перевезень був опорним, необхідно і достатньо, щоб із базисних клітинок не можна було скласти замкнутий ланцюжок (іншими словами: з комунікацій, які відповідають базисним клітинкам, не можна було скласти замкнутий маршрут).

Теорема 4.3. Система векторів перевезень Е лінійно незалежна тоді і тільки тоді, коли з клітин, які відповідають векторам системи Е, не можна скласти замкнутий ланцюжок (цикл).

Що таке базис опорного плану?

Базисом опорного плану Xоп ТЗ вважатимемо будь-яку систему з m + n –1 лінійно незалежних векторів перевезень Pіj , яка містить усі вектори, що відповідають додатним перевезенням

Як подолати виродженість опорного плану?

Щоб подолати виродженість, використовують метод введення штучних нульових перевезень (ε-метод). Це дозволяє додати необхідні клітинки до опорного плану без зміни рівноваги постачання і попиту.

Опишіть алгоритм методу північно-західного кута побудови ОП.

Побудова опорного плану ТЗ методом північно-західного кута Назва методу пов’язана з тим, що на кожному кроці визначавеличи ої) незаповненої прямокутної таблиці перевезень. На початку першого кроку таблиця перевезень є незаповненою, окрім стовпця запасів та рядка потреб. Для першої ітинки (1, 1) розглядаємо величини a1 і b1. Можливі випадки:

• a1 > b1 – потребу b1 можна задовольнити за рахунок запасу a1 (x11 = b1), отож з інших пунктів Ai (i = 2, 3, …, m) у пункт B1 завозити вже не треба нічого (x21 = x31 = … = xm1 = 0) – викреслюємо перший стовпець. На місці a1 запишемо a1 ′ = a1 – b1.

• a 1 < b1 – увесь запас a1 вивозимо у пункт B1 (x11 = a1), задовольняючи лише частину його потреб. Тоді x12 = x13 … x1n =0 – креслюємо перший рядок. На місці b1 запишемо b1 ′ = b1–a1.

• b = a1 = x11 – потреба і запас збігаються. Тоді x21 = x31 = … = = xm1 = x12 = x13 =… x1n =0 – викреслюємо перший стовпець і перший рядок
Отже, в усіх випадках приймаємо x11 = min(a1; b1).

Опишіть алгоритм методу мінімального елемента побудови ОП.

мінімальний елемент

Опишіть алгоритм методу Фоґеля побудови ОП.

На довільному кроці методу:

Сформулюйте і доведіть теорему про оптимальність плану ТЗ.

Для того, щоб деякий план Х T3 був оптимальним, необхідно і достатньо, щоб йому відповідала система із m+n чисел v1, v2, …, vn, u1, u2, …, um, для якої:
vj – ui ≤ cij, (j=1,n ; i = 1,m ) (4.12)
vj – ui = cij для тих (i, j), що x ij > 0 (4.13)

Опишіть алгоритм попереднього кроку методу потенціалів

На попередньому етапі необхідно виконати такі дії:

Опишіть алгоритм основного кроку методу потенціалів

. Основний етап має три кроки:

. Наведіть формальну постановку задачі про призначення

Задача про призначення є окремим випадком транспортної задачі, в якій необхідно призначити 𝑛n працівників для виконання 𝑛n завдань, причому кожен працівник має виконувати рівно одне завдання, а кожне завдання має бути виконане рівно одним працівником. Метою є мінімізація загальних витрат або максимізація загальної ефективності призначень.

Опишіть алгоритм угорського методу розв’язування задачі про призначення.

Основна ідея угорського методу полягає у переході від початкової матриці вартостей С до еквівалентної матриці С* з невід’ємними елементами і системою n незалежних нулів (сукупністю нульових елементів матриці, з яких жодних два не належать одному і тому ж рядку або одному і тому ж стовпцю). У задачі про призначення розв’язок Х має містити n одиниць, з яких жодні дві не належать одному і тому ж рядку або одному і тому ж стовпцю. Отож, якщо n одиниць розв’язку Х розташувати відповідно до розташування незалежних нулів, то отримаємо допустимий розв’язок задачі про призначення. Цей розв’язок слугуватиме оптимальним розв’язком, оскільки йому відповідатиме нульове значення функції мети, яке не можна далі зменшити.

Опишіть алгоритм розв’язування ТЗ за критерієм часу

критерій часу