MATH101 Memorize

Volume of a sphere

V = 4/3 * πr³

Area of a sphere

S = 4πr²

Circumference of a Circle

C = 2πr

Area of a circle

A = πr²

Quadratic Formula

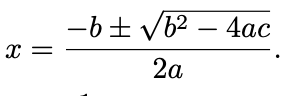
Trig Functions

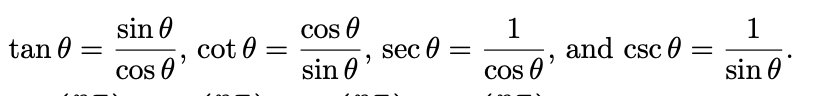
Special Triangles

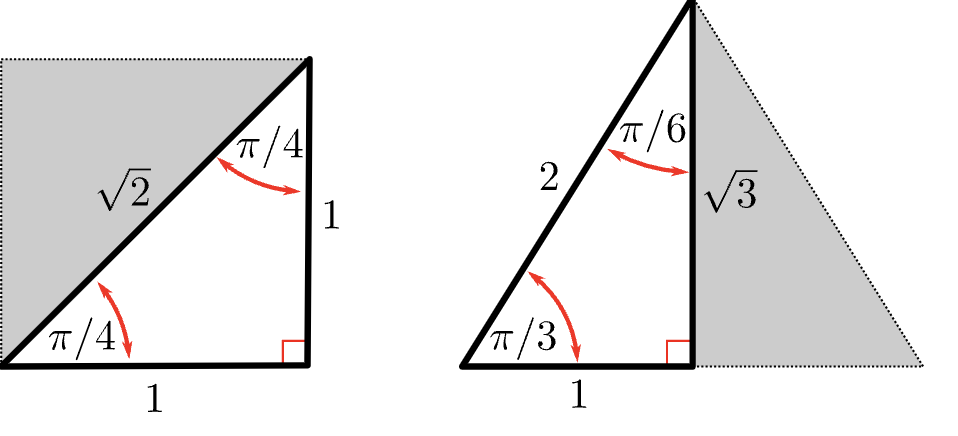
Riemann Sum Right and Left Hand

Right hand: xi

Left hand: x1-1

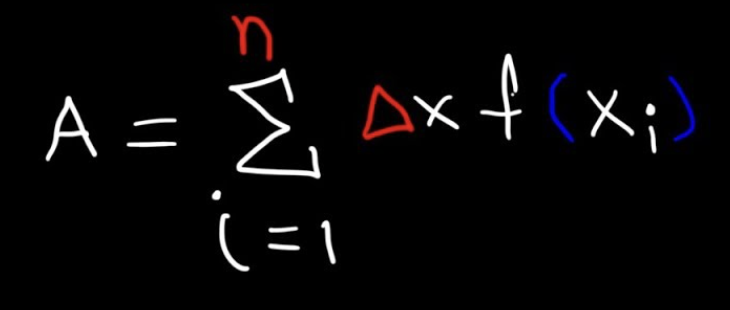
Trapezoidal Rule

delta x = b-a/n n:

number of trapezoids

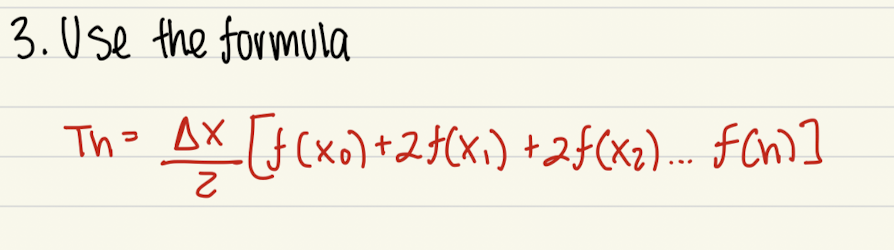
FTC1

This says that the derivative of the integral (function) gives the integrand; i.e. differentiation and integration are inverse operations, they cancel each other out. 

FTC2

Lebniz Rule Formula

Integral = uv - ∫vdu

Pythagorean Identities

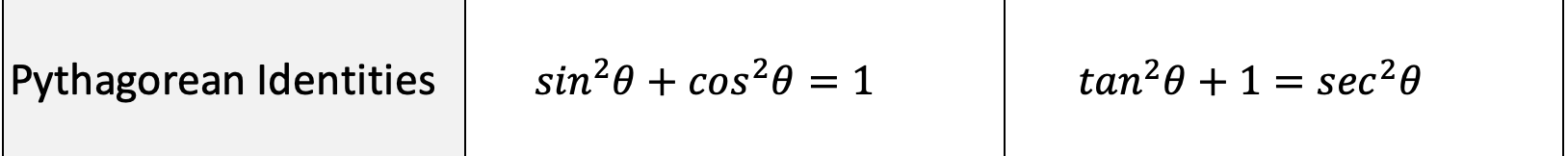
Derivative Identities

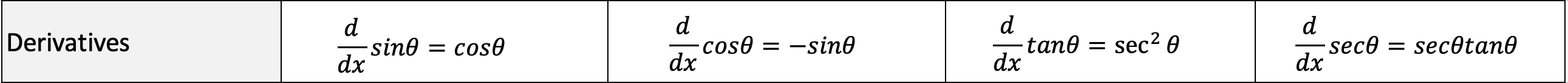
Squared Identities

Sin Sub

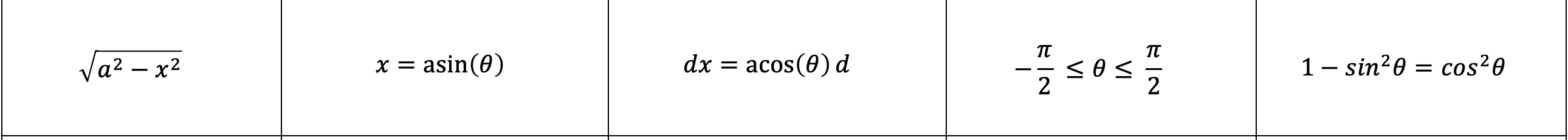
Tan Sub

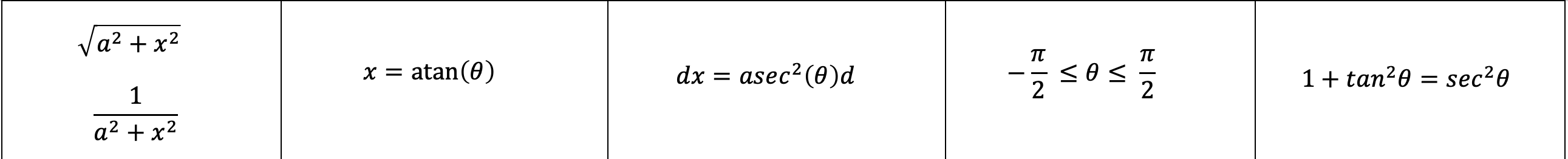
Sec Sub

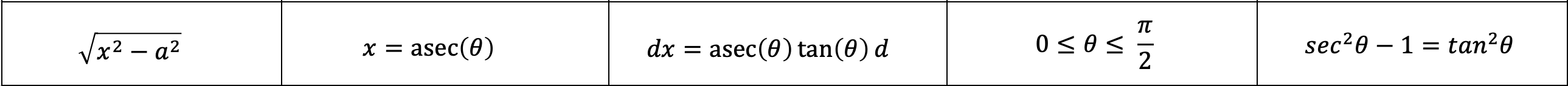
simpsons rule

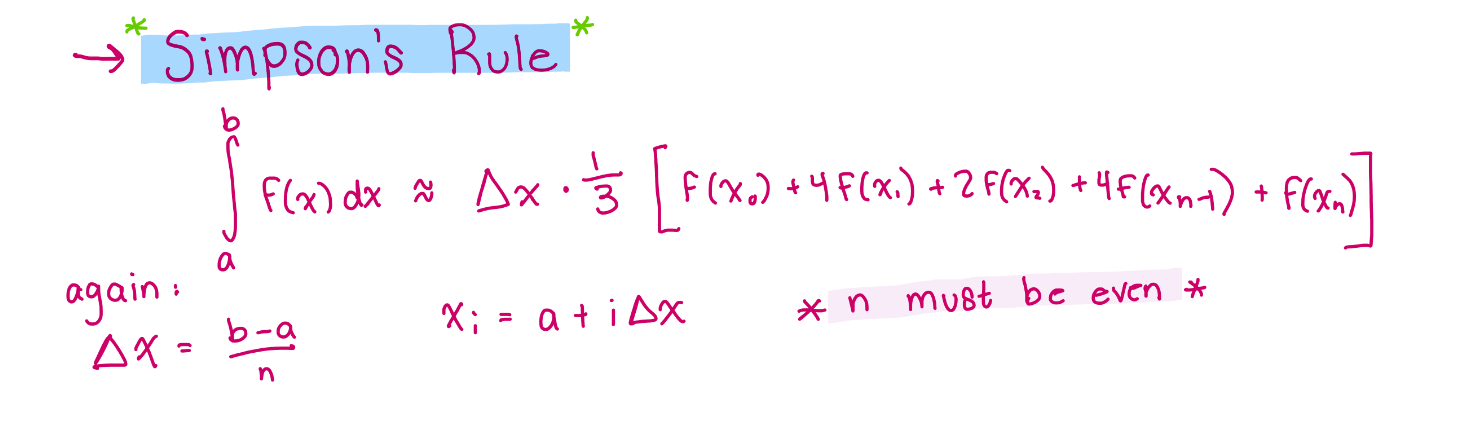
Midpoint reiman

Probability Formula

• Integrating from bound to bound must equal 1.

• PDFS must be greater than or equal to 0

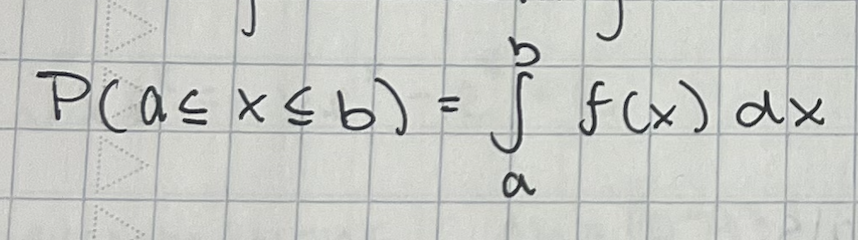
sum of geometric series

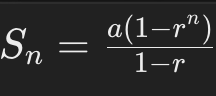
taking the limit of geometric series

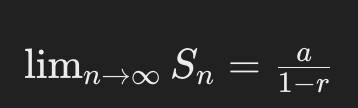
Divergence test

Taking the limit of an (an is the function in the series)

if lim ≠ 0 it diverges

if lim = 0 inconclusive

identifying ratio test

p series test

Telescoping Series Test

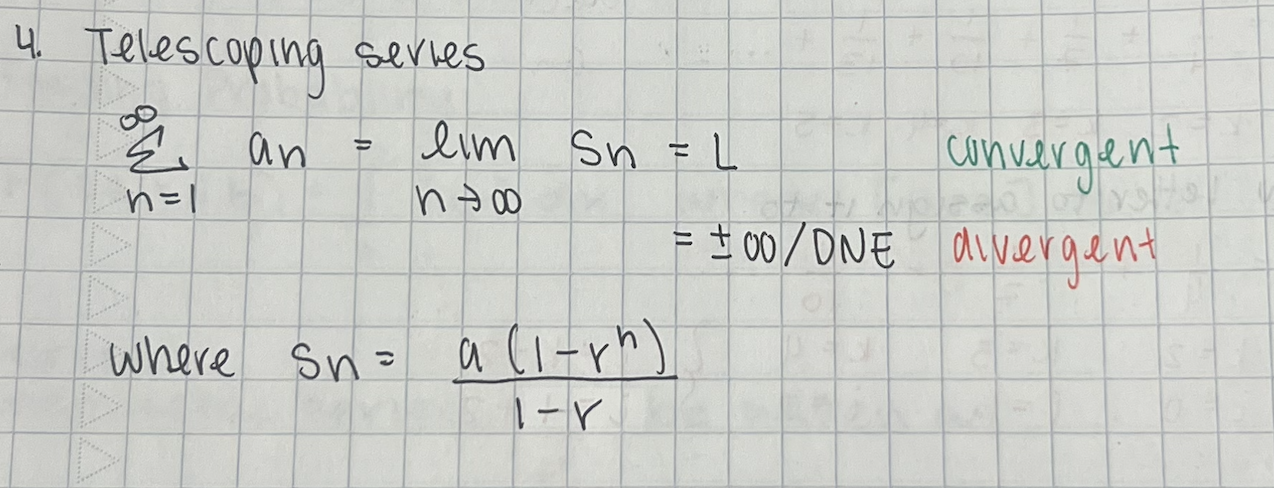
integral test

ratio test

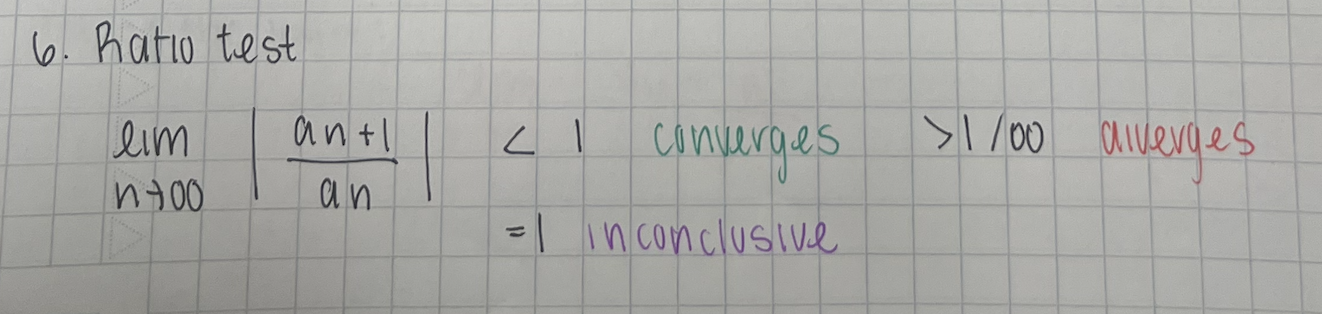
root test

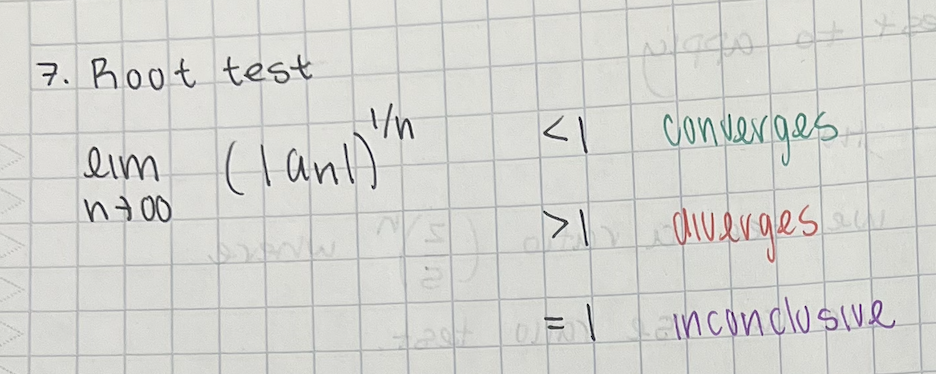
Direct comparison test

Alternating Series Test

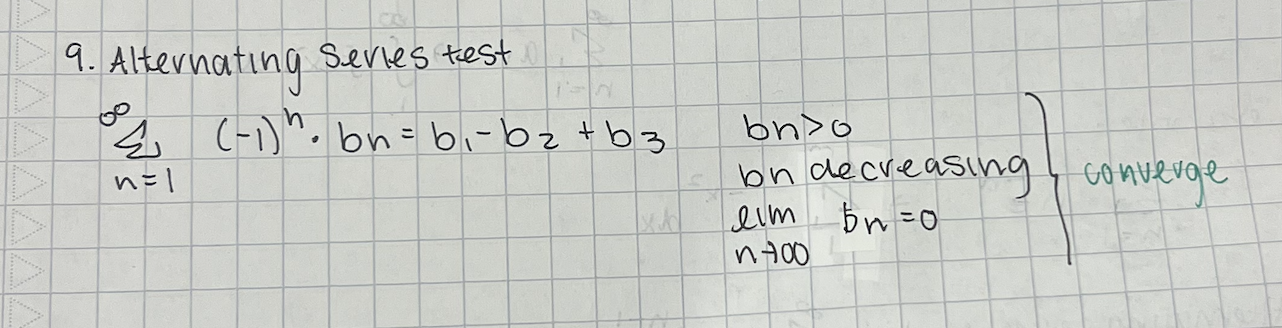
Geometric Series Test

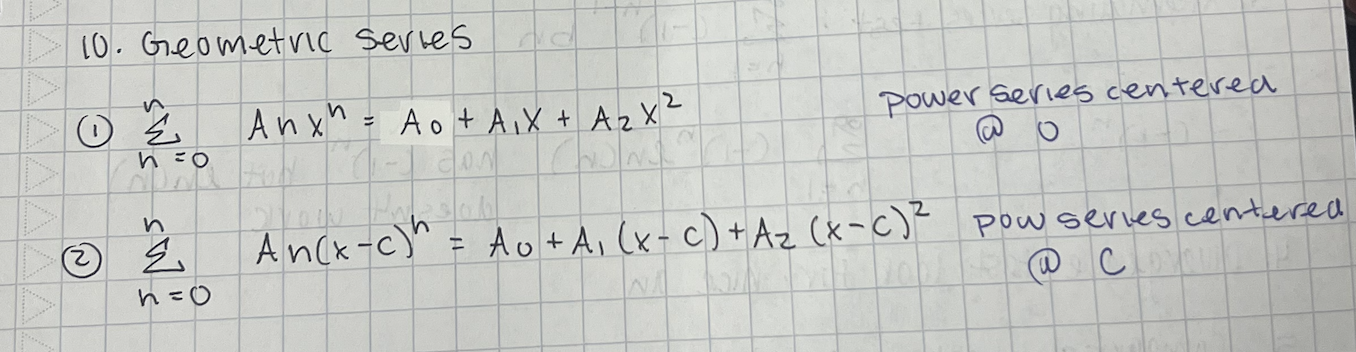
Choosing which test: 1. ratio

look for a clean ratio to the power of n

Choosing which test: 2. alternating series

look for (-1)^n

Choosing which test: 3. divergent series

look for a clean an

Choosing which test: 4. direct comparison and limit comp

ignore factorials

look for nice fractions

Choosing which test: 5. root test

look for equations to the power of n

Choosing which test: 6 ratio

look for factorials

radius of convergence three conditions

ratio(an+1) / (an)

< 1 interval converge

= 0 all x values

= inf only to center

center is where (x-a) in the function where a is the center

check end points by pluging in for x in original series and seeing if it converges or diverges

formula for derivatives taylors series (must get power series representation first)

f^m(0)

______ = the part of your series which is not x^m. solve for f^m

m!

taylor series general formula

where a is the center

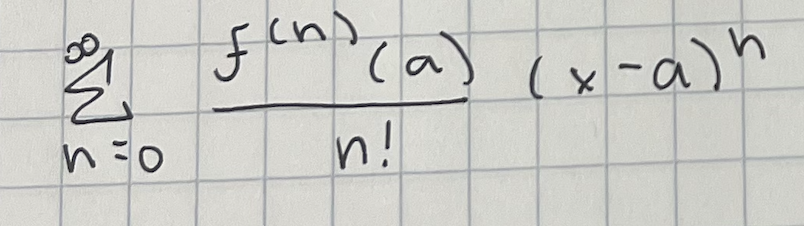
expected value formula PDF

e(x) = integral from your bounds of f(x) * x