Bias-Variance Trade-Off (Pt.1)

What is the equation for overall expected test MSE in relation to variance and bias?

E(y_0 - \hat{f}(x_0))^2 = Var(\hat{f}(x_0)) + [Bias(\hat{f}(x_0))]^2 + Var(\epsilon).

How can we compute the overall average test MSE?

By averaging E(y_0 - \hat{f}(x_0))^2 for each x_0 of multiple training sets.

What does a model with minimal MSE need?

low variance and low bias.

What is Variance in the context of a model?

The amount we expect the model \hat{f} to change if we use a different training set.

What is a quality of Variance?

It is inherently non-negative.

What is a characteristic of Bias?

It is inherently non-negative.

What is a characteristic of a model with high variance?

Small changes in a dataset can make drastic changes in \hat{f}.

What is the relationship between flexibility of a model and its variance?

The more flexible the model, the higher the variance tends to be.

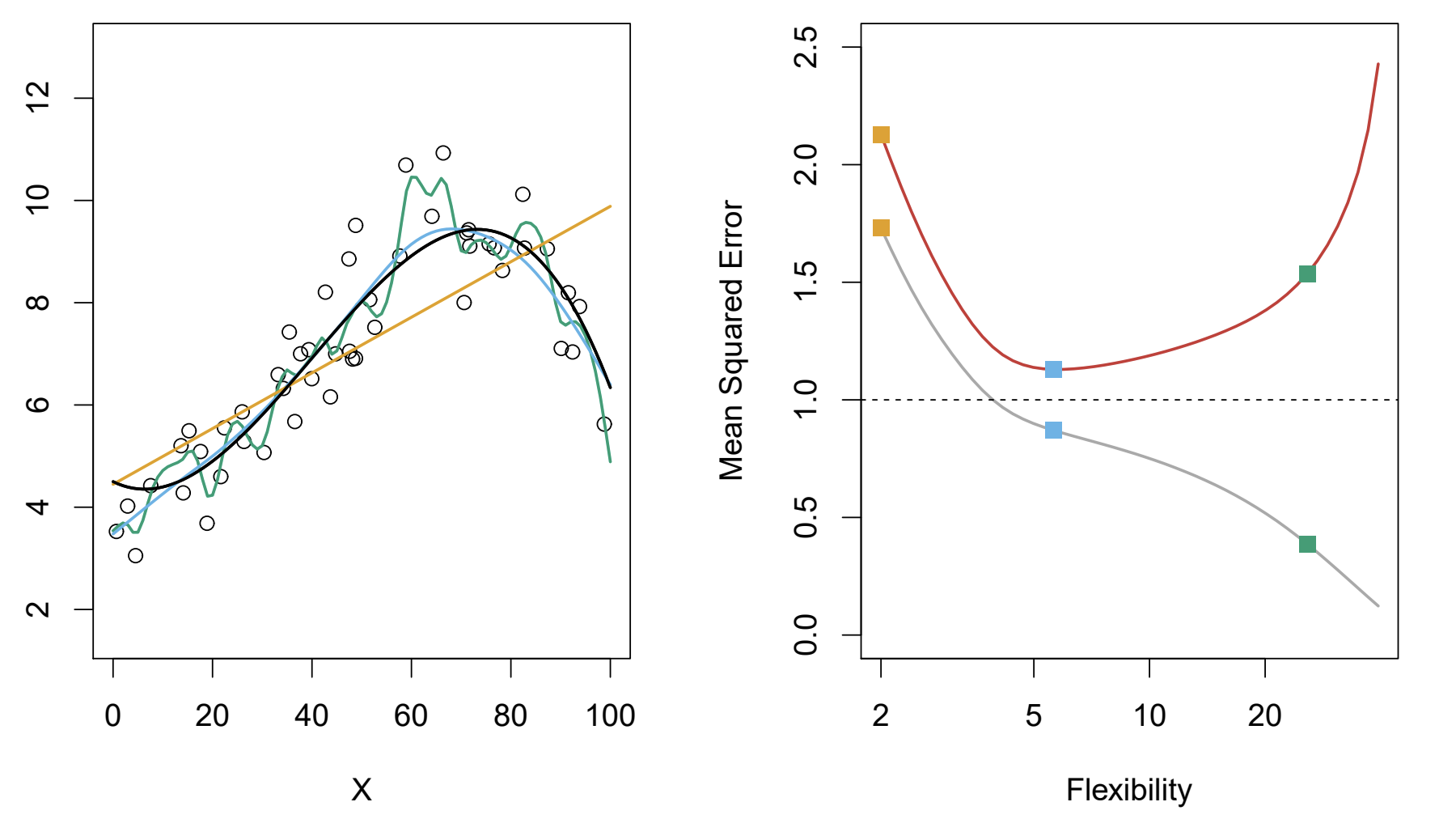
What color model has the lowest variance according to the graph described?

The orange model since it is relatively inflexible compared to the green and blue lines.

What is Bias?

The error introduced by trying to approximate a really complex problem with a much simpler model

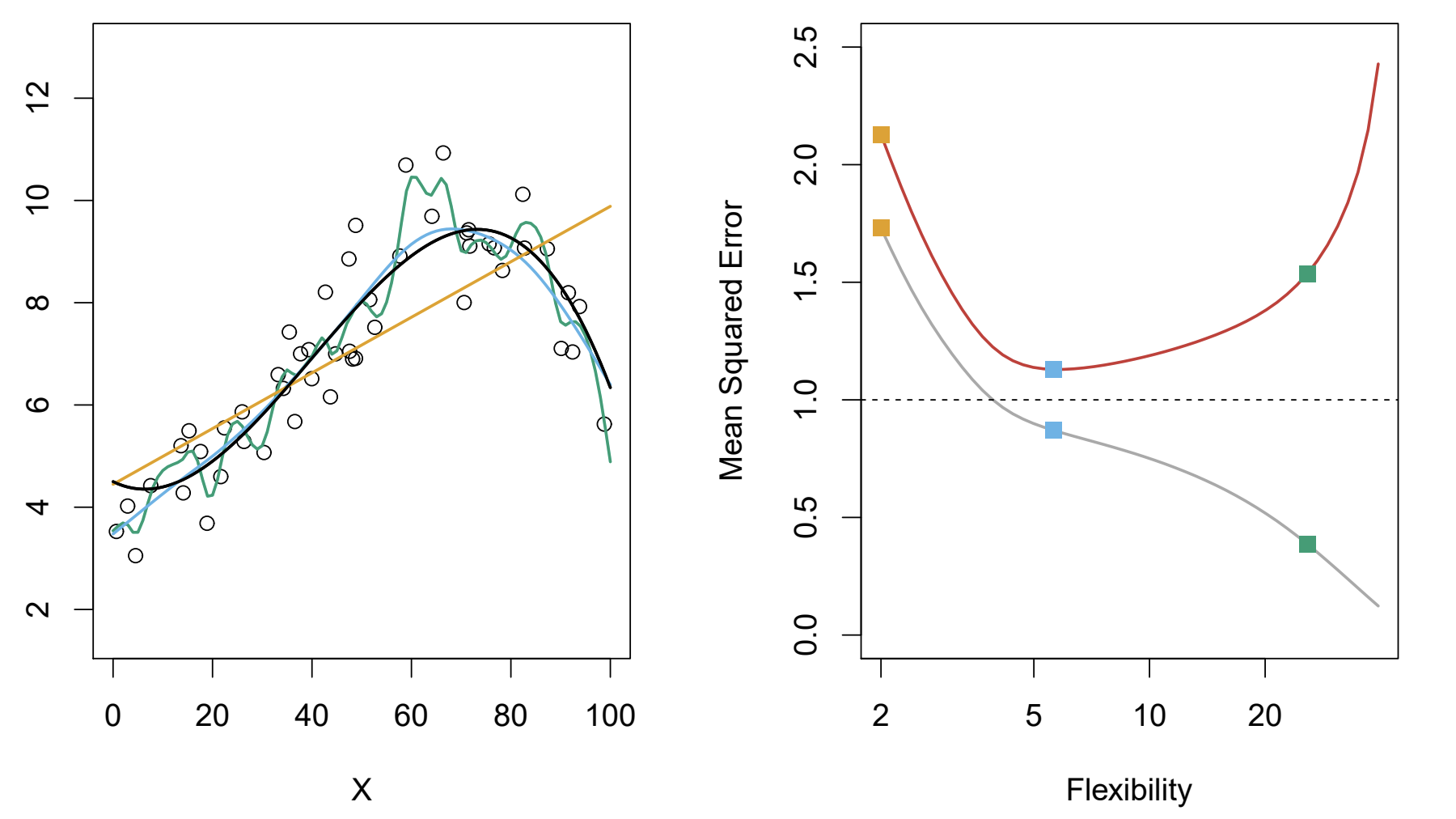
Which color model has the highest bias?

orange

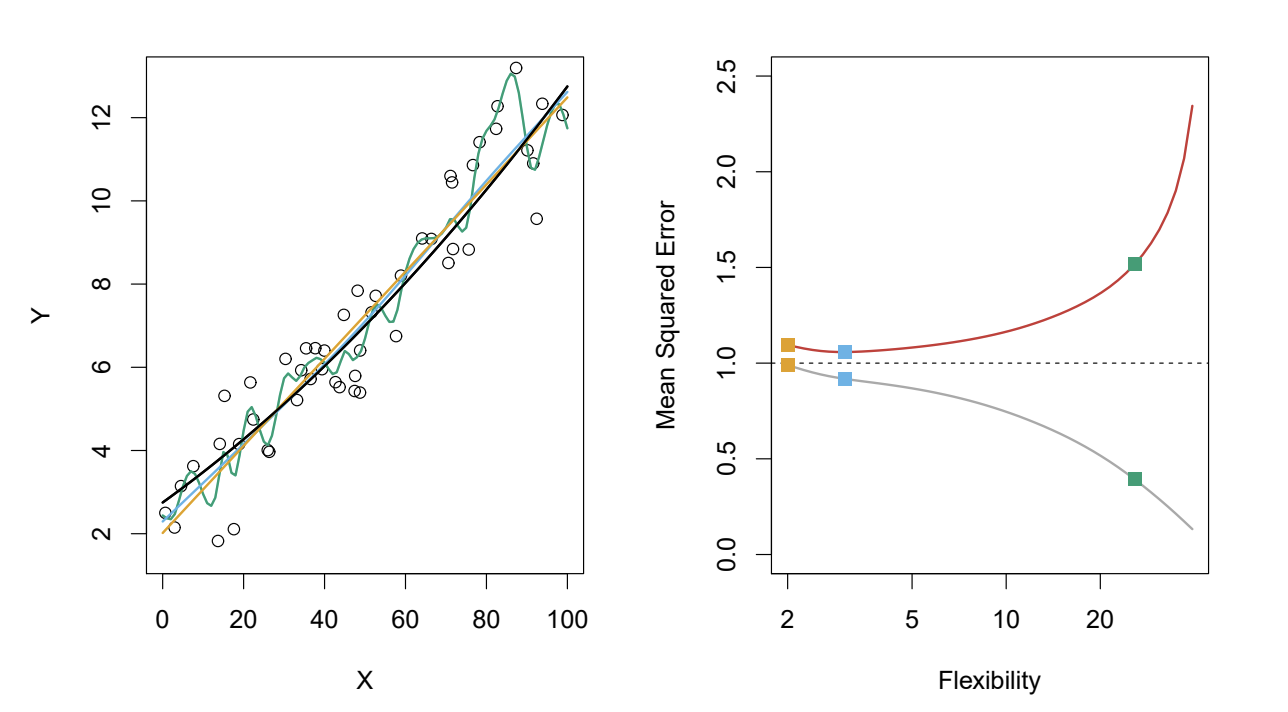
What can be said of all the models here?

They have relatively low bias

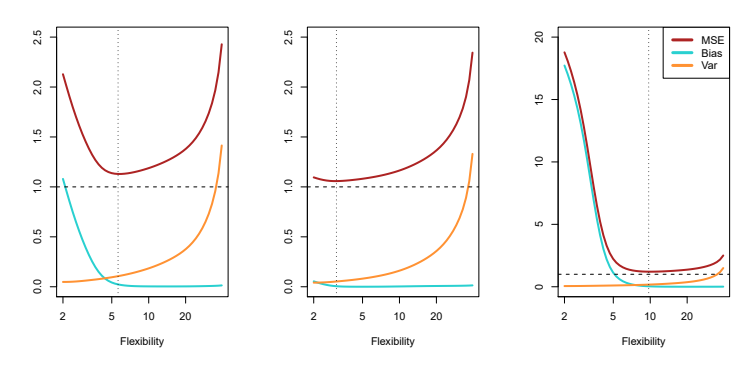
In each of the test MSEs of the image what can be inferred about the relationship between flexibility and bias?

As model flexibility increases, bias decreases, allowing for better fitting of complex data patterns.

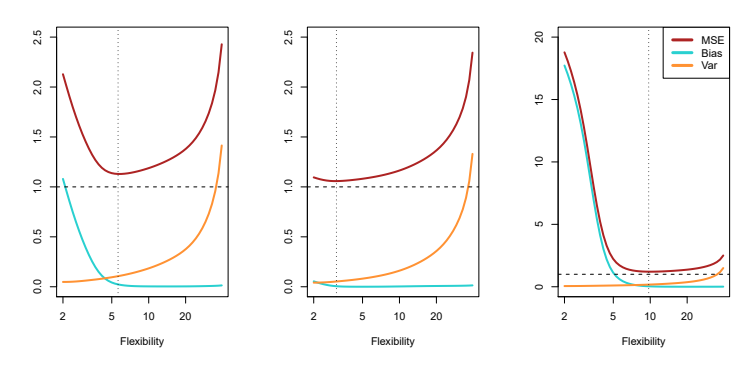
What is a general rule that can be inferred from the graphs about flexibility, variance, and bias of a model?

A general rule is that as model flexibility increases, variance tends to increase while bias decreases.

What is bias-variance tradeoff?

The bias-variance tradeoff is a fundamental concept in machine learning that describes the balance between the error introduced by bias, which can cause an algorithm to miss relevant relations in the data, and the error introduced by variance, which can cause an algorithm to model the random noise in the training data rather than the intended outputs.