Math Section- SAT Prep

All information regarding the math section of the SAT

Question Type Breakdown

70% problem solving (15-16 Q per module)

30% word problems (6-7 Q per module)

Content Breakdown

35% Algebra (7-8 Q)

35% Advanced Math (7-8 Q)

15% Problem Solving and Data Analysis (3-4 Q)

15% Geometry and Trig (3-4 Q)

Ballparking Strategy

Look for the answers that are the wrong size. So something that overestimates or underestimates the correct answer. Eliminate them

Bite Sized Pieces Strategy

Take each step one at a time and try to eliminate answers

Word Problems Basic Approach

1. Read the final question and write down key words. Pay attention to exactly what it’s asking for

2. Let the answer point the way. What is present in the answer choices?

3. Work in bite sized pieces

4. Use POE

Calculators are good for…

1. Arithmetic

2. Decimals

3. Fractions

4. Square roots

5. Percentages

6. Graphs

Directions for the SRQ

1. Enter one correct answer

2. You can enter up to 5 characters for a positive answer and up to 6 (including the negative sign) for a negative answer

3. Enter the decimal equivalent if your fraction doesn’t fit the designated space

4. Round your decimals to the fourth digit if you can’t fit it in (ex: 0.666) four digits

5. Fractions that are like 3 ½ must be improper so 7/2

6. No symbols, like percentage

Arithmetic on the SAT

1. Addition

2. Subtraction

3. Multiplication (product)

4. Division (quotient)

5. Raising to a power

6. Finding a root

The Distributive Law

If you are multiplying the sum of two numbers by a third number, you can multiply each number in your sum individually 2(3+2)= 6+4

Fractions

FLIP THE SECOND FRACTION WHEN DIVIDING

Exponent Rules

1. Exponents with the same base can be multiplied like:

   2³ × 2⁵= 2³⁺⁵ because you are adding

2. Exponents with the same base can be divided like:

   2⁵/2^{3= 2}5 because you are subtracting

3. When raising a base to two powers multiple the powers

   (2³)⁴=2¹²

4. If two exponents with the same base equal each other, you can set the exponents equal to each other

   a^2y=a¹⁰—> 2y=10

5. MADSPM= Multiply—> Add, Divide—> Subtract, Power—> Multiply

Square Root General Rules

1. If you square or cube a number greater than one it becomes larger, ex: 2²=4 , 2³=8

2. If you square or cube a number less than one it becomes smaller, ex: (1/2)³= (1/8)

3. Square roots can’t be negative on the SAT

Square Root Rules

1. (√x)(√y) = √xy

2. √x/y= √x/√y

3. √x= positive root only

Negative and Fractional Exponents

Negative Exponents are a fancy way of writing reciprocals

x^-n= 1/xⁿ

Fractional exponents are a fancy way of taking roots and powers

x^y/z=^z√x^y

An important note about rational equations

With radical expressions, you are likely to find extraneous solutions. You have to account for those in your answer

One solution, no solution, infinite solutions in terms of slope

1. If two equations represent lines with different slopes, there is one solution

2. If the lines have the same slope but different y intercepts there is no solution

3. If the lines have the same slop and y intercepts then there are infinitely many solutions

A note about inequalities

If you multiply or divide both sides of an inequality by a negative number, the direction of the inequality symbol changes

She will order no more than three times as much blue ribbon as red ribbon

In sentences like these, the second word or second term is what you attach that three times onto despite how it sounds

3r ≥ b

Digital SAT Favorites Quadratic Equations

The three equations they use the most often

1. (x+y)(x-y)=x²-y²

2. (x+y)²=x²+2xy+y²

3. (x-y)²=x²-2xy+y²

Quadratic formula

Negative b plus minues square root b squared minus four ac over 2a

The Root of the Problems

Sometimes you will be asked for the sum or a product of the roots of a quadratic. You can use the quadratic formula or use these equations

sum of the products = -b/a

product of the products= c/a

Discriminants and their rules

The discriminant of the quadratic formula is what is under the root, so b²-4ac

• If the discriminant is positive, the quadratic has two real solutions

• If the discriminant equals zero, the quadratic has 1 real solution

• If the discriminant is negative, the quadratic has no real solutions

Growth and Decay

When the growth or decay rate is a percent of the total population

final amount = original amount (1 ± rate)^{number of changes}

When the growth or decay is a multiple of the total population

final amount = original amount (multiplier)^{number of changes}

PITA Basic Approach

PITA stands for plug in the answer. Sometimes, it’s best to avoid algebra on the SAT and just plug in answers instead

1. Rewrite the answer choices and label them

2. Start with the middle answer choice

3. Look for something in the question that tells you what must happen for the answer to be correct

4. Once you find the write answer, STOP

Use PITA if there are numbers in the answer choice, if the questions asks for a specific amount, or you need to use algebra to solve

Avoid plugging in zero and one

Plugging in your own numbers

1. Pick numbers for the variables in the question

2. Use your numbers to find an answer to the questions. Circle your answer

3. Plug your numbers for the variables into the answer choices and eliminate choices that don’t equal the answer you found in step 2

Meaning in Context Questions

Gives you an equation and makes you interpret the context of the situation

Basic Approach for Meaning in Context Questions

1. Know which part of the equation you’re being asked to identify

2. Rewrite the question, replacing parts you can identify with labels

3. Eliminate answers that go against what you label

Function

A machine to produce ordered pairs. If a question gives you information about what comes out of a function and asks what goes in, its a PITA question

Slope

• Remember that a negative slope represents a graph going down

• Standard form: ax+by=c. The slope of the line using tis form is -a/b, the y intercept of the line using this formula is c/b, the x intercept of the line is c/a

• Parallel lines have the same slope, Perpendicular lines have a negative reciprocal of the other lines slope (so one slop would be 3 and the other would be -1/3)

• Infinitely many solutions= same slop and int

• No solutions= same slop diff int, parallel

Transformations

f(x)= no shift

f(x)+c= shift c units up

f(x)-c= shift c units down

f(x+c)= shift c units to the left

f(x-c)= shift c units to the right

Parabolas

Standard form: y=ax²+bx+c. If a is positive the parabola opens upward. If a is negative the parabola opens downward

The factored form of a parabola is: y=a(x-r1)(x-r2) where r1 and r2 represent the x intercepts

Vertex form: y=a(x+h)²+k where (h,k) is the vertex or the maximum (a is less than 0) or minimum (a is greater than 0)

To convert from standard to vertex use the formula h= -b/2a then plug into the vertex form

Circles

The equation of a circle is (x-h)²+ (y-k)²=r²

The center is (h,k), the radius is r, and when you are finding the center make sure to switch signs so if its x+h that means its negative h and vice versa

If you are asked for the radius of a circle given a graph look for the maximum and minimum and subtract and divide by 2

Ratios and proportions

Ratios are comparisons. Ratios make you combine the parts to get the whole

ex: There are 24 students and the ratio of boys to girls is 2:1. How many boys are there and how many girls are there?

2:1—> 2+1=3. Take this added number and divided the amount of students total by it so 24/3= 8

Now multiply the original ratio by eight to get 16 boys and 8 girls

Percentages

Fractions with a denominator of 100

part/whole= x/100= x %

Decimal, percentage, fraction conversion to memorize

1. 0.01 = 1/100 = 1%

2. 0.1 = 1/10 = 10%

3. 0.2 = 2/10 = 20%

4. 0.25 = ¼ = 25%

5. 0.5 = ½ = 50%

6. 0.75 = ¾ = 75%

Converting between decimals and percentages

To convert percentages to decimals move the point two places to the left. To convert decimas to percentages move the point two places to the right

Converting between fractions and percentages

To go from fraction to percentage, simply divide the fraction using a calculator and use the decimal you find to calculate the percentage. To convert percentages to fraction, take the percent and put it over 100 and simplify

Average

Mean, numbers added and divided by the number of numbers

Averages formula: T= AN. Where T equals the total number of all the numbers, A is the average, and N is the number of numbers.

Median, Mode, and Range

Median: Number that is exactly the middle of the list when the list is arranged from smallest to largest

Mode: In a group of numbers, the number that appears the most often

Range: The difference between the greatest and least number in a set of numbers

Margin of Error

It is a range of percentages. A margin of error gives a range for random sampling errors in a survey or poll. It indicates how much the results might change if the poll were repeated or if the entire population were asked instead of a random sample

Standard Deviation

Measure of how numbers are distributed around the mean. When the numbers are more spread out around the mean, the standard deviation is greater. When the numbers are closer to the mean it is smaller

Probability

The mathematical expression of the likelihood of an event. To express the probability of any event you count the number of possible outcomes, the number of outcomes that gives you what you want, and arrange it as a fraction

Probability of X= #of outcomes that gives you what you want/ total number of possible outcomes

The largest a probability can be is 1, total certainty. The lowest is 0, never happening. You can find probability that something will Not happen by subtracting the probability that it will happen from 1

Rates

D= RT for distance

W= RT for work

Geometry Basic Approach

1. Draw a figure

2. Label

3. Write down formulas

4. Ballpark

Plugging in is good!

Lines and Angles

1. A circle contains 360^o

2. Think of circles with angles. An angle is formed where two lines touch each other at a point, so view that point as the middle of the circle

3. A line is 180^o angle

4. When two lines intersect, four angles are formed

   ex: X. You see how if I were to draw a circle in the middle of the X, four angles would be formed.

5. When two lines intersect, the angles opposite each other will have the same measure (vertical angles). Look at the diagram, the angles 1 and 3 will be the same measure and angles b and d with be the same measure. It will total to 360^o

6. If two lines are perpendicular to each other, each of the four angles formed are 90^o

   ex: +, each angle formed by the plus, so two perpendicular lines, will be 90 degrees

7. Transversals, when two parallel lines are cut by a third line, all of the big angles are equal, and the sum of any big and the and small angle is 180^o. So remember a-b-b-a. The b angles are the small angles and equal each other, and the a angles are the big angles and equal each other. Add a + b and you get 180

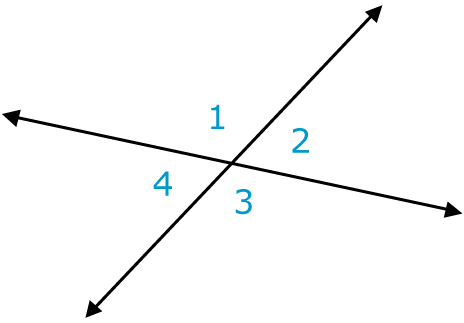
Triangles

Every triangle contains 180^o. All the interior angles add up to make that

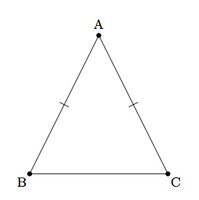
Isosceles Triangles

Triangles in which two of the sides are equal in length. SO in triangle ABC, sides AB= AC and angles c and b equal each other

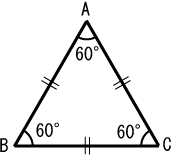
Equilateral Triangles

Triangles where all three sides are equal in length. And each angle is 60^o exactly. So in triangle ABC, AB=BC=AC

Right Triangles

A right triangle is a triangle in which one of the angles is a right angle (90^o). Some right triangles are also isosceles, so the angles are 45-45-90

Area and perimeter of triangles

The perimeter of a triangle is the sum of the lengths of the sides. The area is ½ bh

Trig Ratios

SOHCAHTOA
sin= opposite/ hypotenuse

cos= adjacent/ hypotenuse

tan= opposite/ adjacent

remember that trig ratios are subjective based on the triangle, and they only apply to right triangles

Special Right Triangles

Here are some special right triangles that you will often see in questions regarding Pythagorean theorem, it is easy to memorize these rather than solving them out with a²+b²=c²

3-4-5

5-12-13

6-8-10

10-24-26

There are two types of special right triangles that have a specific ratio of angles. these are 30-60-90 triangles and 45-45-90 triangles. The sides of these triangles always have the same ratios

For 45-45-90: The triangles have an x-x-x√2 relationship. Where the two legs are x and the hypotenuse is x√2

For 30-60-90: The triangles have a x-x√3-2x relationship. Where the two legs are x and x√3, and the hypotenuse is 2x

Two triangles are similar when 1 of the following is true…

• Remember: Similar means set up a proportion

1. All three angles of the triangle are congruent (AAA)

2. Pairs of sides of the triangle are in proportion, and the angle between those sides are congruent (SAS)

3. All three sides of one triangle are in the proportion to the corresponding three sides of the other triangle (SSS)

Trigonometric ratios are the same in similar triangles. So if one triangle has a cos of x, so does the other

Two triangles are congruent if one of the following is true…

1. All three sides are equal (SSS)

2. Two pairs of angles and the side between them are equal (ASA)

3. Two pairs of sides and the angle between them are equal (SAS)

4. Two pairs of angles and the side that isn’t between them are equal (AAS)

If two shapes are similar, they are always congruent. But its not the same the other way around

Circles

1. The circumference of a circle is 2πr or πd

2. The area of a circle is πr²

3. A tangent is a line that touches a circle at exactly one point. A radius drawn from that tangent point forms a 90^o angle with the tangent

Arcs and Sectors

1. Arcs are portions of a circles circumference

2. Sectors are portions of its area

   arc length/ 2πr = sector area/ πr² = central angle/ 360^o

3. Minor arc/ sector: Has a central angle of less than 180

4. Major: Has a central angle of greater than 180

5. Equation for arc length: s=rtheta. Where s is the arc length, r is the radius, and theta is the angle. s/r equals the angle. s/ theta equals the radius

Converting degrees to radians and radians to degrees

degrees to radians, multiply the degree by π/180

radians to degrees, multiply the radians by 180/π

Rectangles and Squares

1. The perimeter of a rectangle is the sum of the lengths of the sides

2. The area of a rectangle is the length times the width

3. A square is a rectangle whose four sides are all equal

4. Rectangles and squares can only have a 90^o angle

5. the volume of a sphere is 4/3 πr³

Each research paper had five more pages than each short story

s+5=r, although you might be tempted to do the other way around, remember that that five always goes to the second term