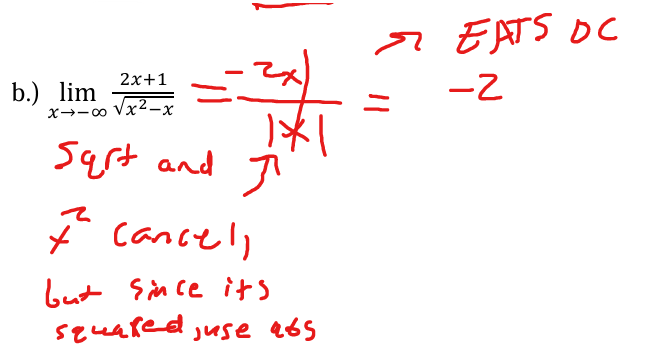AP Calculus AB Unit 1

Conclusion Statement:

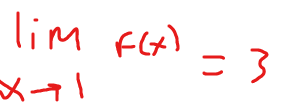
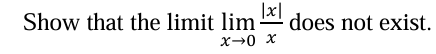
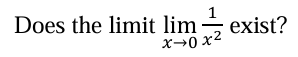
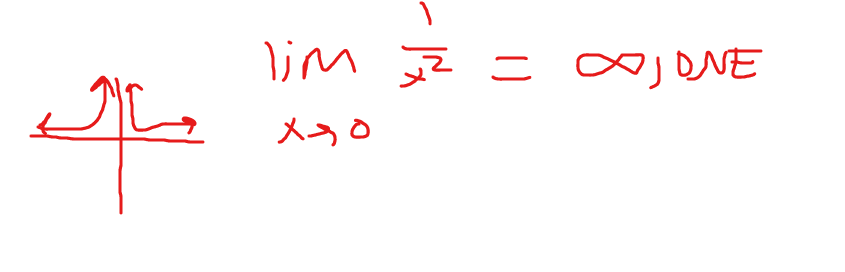
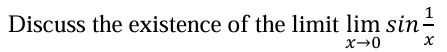
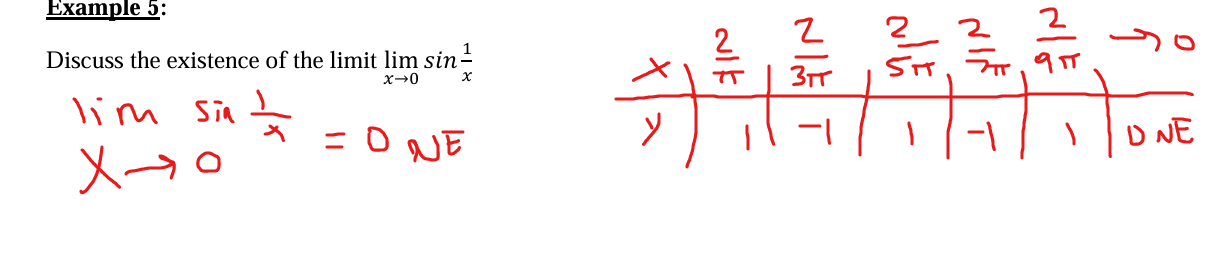
ln(e) = ?

1

ln(1)

0

ln(0)

undefined

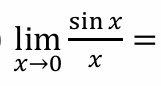
1

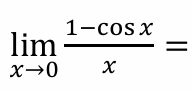
0

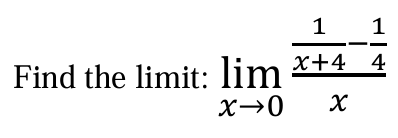
-1/16

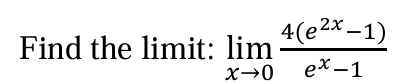
8

Three continuous conditions

f(c) is defined
lim f(x) as x approaches c exists
lim f(x) as x approaches c equals f(c)

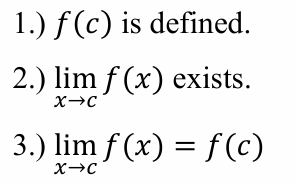
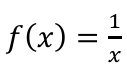
Continuity of this function:

can’t divide by 0, so (-∞,0) U (0,∞)

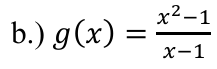
Continuity of this function:

hole at x=1, so (-∞,1) U (1,∞)

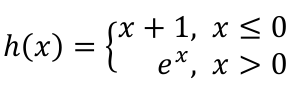
Continuity of this function:

(-∞,∞)

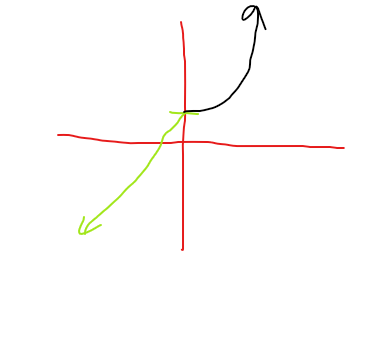
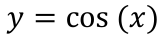
Continuity of this function:

(-∞,∞)

0

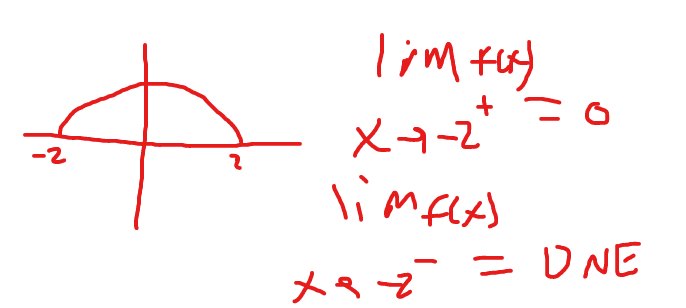
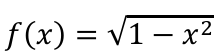
Discuss the continuity of this function:

f(x) is cont. on [-1,1]

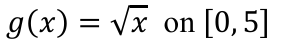
Discuss the continuity of this function:

g(x) is cont. on [0,5]

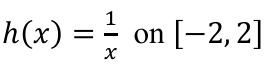
h(x) is cont. on [-2,0) U (0,2]

if f and g are continuous on (-∞,∞), then

fg is continuous (-∞,∞)
f±g is continuous (-∞,∞)
f/g is continuous (-∞,∞), given that the denominator is not 0

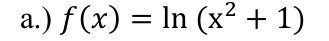
where is composite function continuous

y=x²+1 is cont. on (-∞,∞) and y=ln (x) is cont. on (0,∞), therefore f(x) is cont. on (0,∞)

IVT Theorem states that

If f is continuous on the closed interval [a,b], f(a) ≠ f(b), and k is any number between f(a) and f(b), then there is at least on number c in [a,b] such that f(c) = k

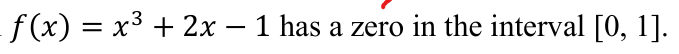
Prove that this function is continuous using IVT

f(x) is cont. on [0,1], since f(0) =1 and f(1) = 2 and -1 < 0 < 2, then by IVT, there is at least one c in [0,1] such that f(c) = 0

in order to give the IVT justification for a table, the question must state that

the function is continuous

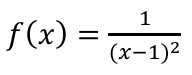
Determine the limit as x approaches 1 from the left and right

∞, DNE

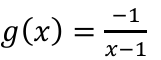
Determine the limit as x approaches 1 from the left and right

DNE

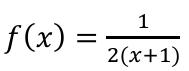
Determine the limit as x approaches -1 from the left and right

DNE

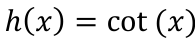
Find the VAs

pi(k)

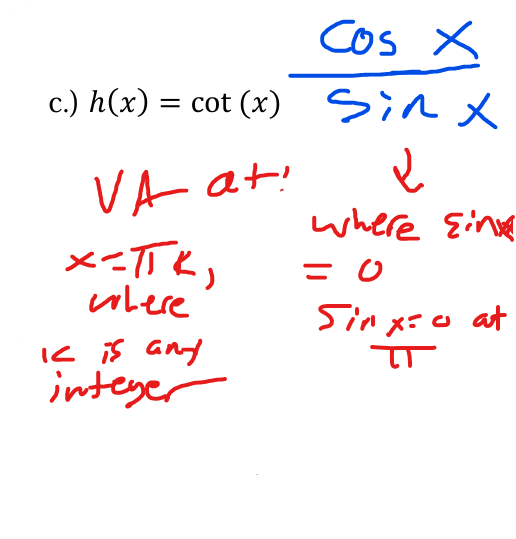
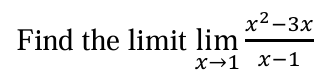
DNE

if you can’t find lim of a function through direct substitution, factoring, or conjugates, and you get b/0, then

solve for the lim as x approaches from both sides (±), the answer should be either ±∞, DNE or DNE

∞

-∞

-∞

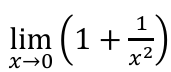
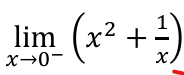
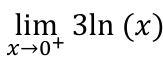
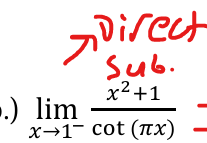
0

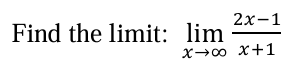
2

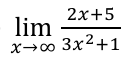
0

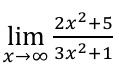
2/3

∞

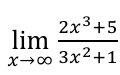
For BOBO and EATS DC you get numbers for answers, but for BOTN you get

either ±∞

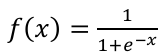
Find both of the horizontal asymptotes

1 and 0

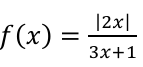
Show that f has different horizontal asymptotes from the left and right

2/3 and 0

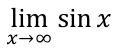
find the limit

DNE

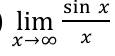
find the limit

0

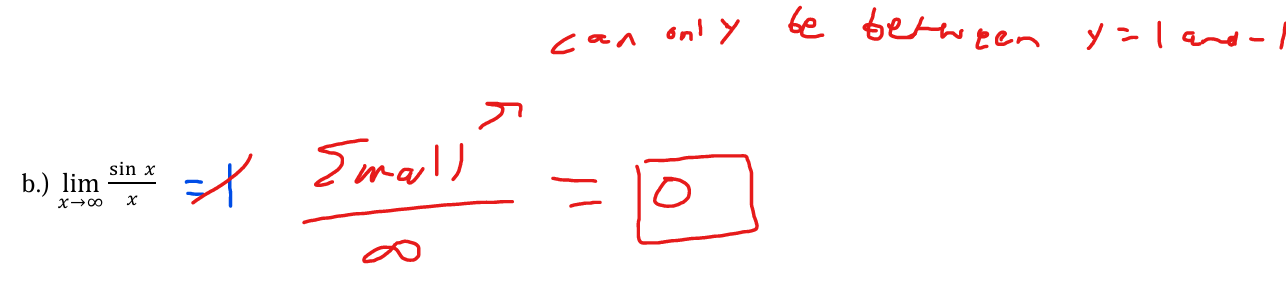
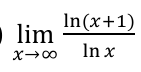
find the limit

1

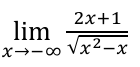
-2